OLS样本估计量抽样分布模拟

1 OLS估计量分布

对于线性回归方程
$$Y={\beta }_0+{\beta }_{1}X+\epsilon$$
利用普通最小二乘法(OLS）估计上述方程参数使的假定(之一)是扰动项$\epsilon$必须满足正态分布，这样才能保证估计量也服从正态分布。当扰动项服从正态分布，如果自变量是确定性的，那么被解释变量也服从正态分布。根据OLS估计量的线性性性质
$${\beta }_1=\sum k_i{Y}_i$$
其中常数列$k_i$一定满足$\sum k_i=0$,$\sum k_i{X}_i=1$。当样本估计量抽样分布知晓后，就可以进行推断统计，包括假设检验和区间估计等。下面通过R语言进行模拟这一过程。

---

2 R语言实现

数据模拟

# OLS抽样分布
# 数据模拟
set.seed(1110)
# 总体容量
N = 5000
ID = seq(1,N,1)
# 自变量
x1 = rnorm(N,2,3)
x2 = rnorm(N,1,2)
x3 = rnorm(N,2,1)
# 残差
e = rnorm(N,0,3)# 直方图与核密度曲线
par(mar = c(2,2,2,2),mfrow =c(1,1))
hist(e,prob = T,col = "blue",main = "残差e分布")
lines(density(e), col="red", lwd=2)# 被解释变量
y = 1 + 2*x1 + 3*x2 + 4*x3 + e
# 被解释变量分布
op <- par(fig=c(.03,.3,.5,.98), new=TRUE)
hist(y,prob = T,col = "red",main = "y分布")
lines(density(y), col = "blue", lwd=2)
box()
par(op)# 合并为数据框
data = data.frame(ID,y,x1,x2,x3)

残差与被解释变量的经验分布如下图

接下来进行样本抽取(简单随机抽样,抽取一次，样本容量为500)

# 样本抽取
sample1 = sample(N,500,replace = FALSE) 
mydata1 = data[sample1,]
# OLS回归
OLS = lm(y~1 + x1+ x2 + x3,data = mydata1)
B = OLS$coefficients
B[1]
B[2]
B[3]
B[4]

现在抽取10000次，样本容量为500

# 参数抽样分布
B1 = numeric()
B2 = numeric()
B3 = numeric()
B4 = numeric()
for (i in 1:10000){sampling = sample(N,500,replace = FALSE) mydata = data[sampling,]OLS = lm(y~1 + x1+ x2 + x3,data = mydata)B1[i] = OLS$coefficients[1]B2[i] = OLS$coefficients[2]B3[i] = OLS$coefficients[3]B4[i] = OLS$coefficients[4]
}
mypar = data.frame(B1,B2,B3,B4)
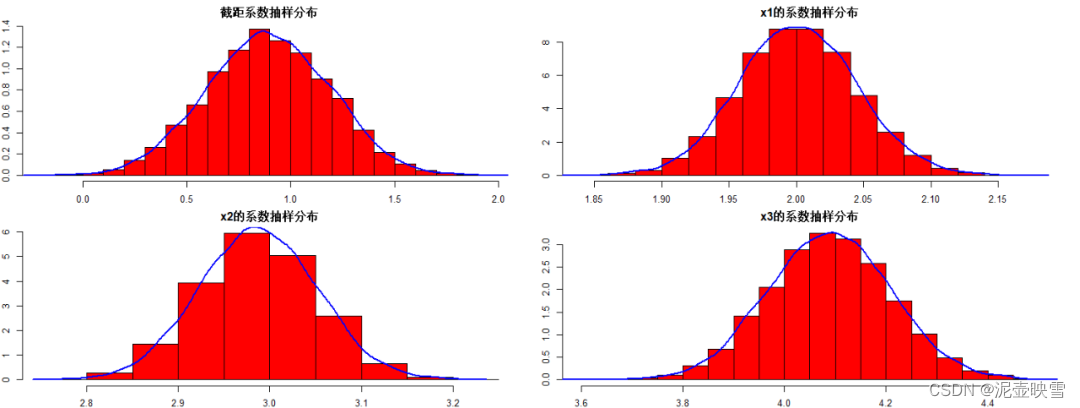
# OLS估计量的线性性质,回归参数也服从正态分布
par(mfrow = c(2,2))hist(B1,prob = T,col = "red",main = "截距系数抽样分布")
lines(density(B1), col = "blue", lwd=2)hist(B2,prob = T,col = "red",main = "x1的系数抽样分布")
lines(density(B2), col = "blue", lwd=2)hist(B3,prob = T,col = "red",main = "x2的系数抽样分布")
lines(density(B3), col = "blue", lwd=2)hist(B4,prob = T,col = "red",main = "x3的系数抽样分布")
lines(density(B4), col = "blue", lwd=2)

各个参数的经验分布如下图：