白化 Whitening
由于图像中像素之间具有很强的相关性,所以用于训练时输入是冗余的。白化的目的是降低输入的冗余性,我们希望通过白化过程使得算法的输入有如下性质:1、特征间相关性较低。2、所有特征具有相同的方差。
z-score白化
将图片调整为平均像素值为0,方差为单位方差的分布。
PCA白化
假设输入数据是冗余的,经过白化处理后:1、特征间相关性较低。2、所有特征具有相同的方差。
第一步和PCA类似(所以叫PCA白化),也就通过降维映射到新的特征空间,这就完成了原始数据的去相关性。第二步就是对新的特征空间的每一维进行方差归一化处理(也就是对各个特征轴上的数据除以对应的特征值,因为特征值就等于数据在旋转后的坐标上对应维度的方差),从而达到各个特征轴上都归一化幅度的结果。
中心化与归一化效果图:

去相关与PCA白化效果图:

白化加速收敛的理由
一种解释是,去相关后的矩阵保留了原矩阵的重要信息(特征值),而过滤到了一些不相关的量。这样一来算是对关键信息的一种增强,由于每个特征更加独立,使得模型更容易训练。
白化的缺点
若使用PCA白化,会涉及到协方差矩阵的计算,计算量较大。
批标准化 Batch Normalization
机器学习的前提是:独立同分布。也就是训练集和测试集满足相同分布,可以获得好的效果。深层神经网络的隐藏层,包括线性变换和非线性激活函数。在面临深度学习的情况时,容易出现的情况是前一个隐藏层的线性变换,在训练的过程中由于参数(w,b)一直在变,导致这个输出的分布不稳定,进而导致在输入到激活函数时不够稳定,这可能导致收敛缓慢、梯度消失等问题(在这篇文章中提到了一些常见激活函数的特性),最后导致整个训练过程收敛缓慢。
这就是“Internal Covariate Shift”问题。它导致网络模型很难稳定地学习规律,收敛较慢。
于是就想,如果在线性变换和非线性激活函数中间搞个什么东西,是不是能够解决上述这个问题?
BN的作者就联想到了白化处理。白化能够加速收敛,那把这个思想扩展到深度学习呢?让每个隐层在线性变换进行一个“白化”处理?于是就萌生了Batch Normalization。
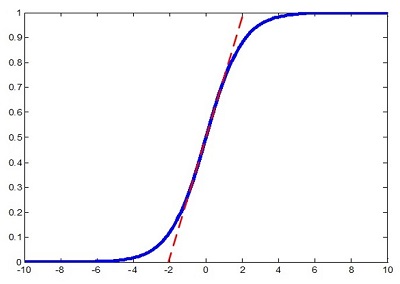
我们在每个隐藏层的线性变换完成后,增加一个BN操作,把分布强行拉回均值为0,方差为单位方差的分布。再将其输入非线性激活函数(比如sigmoid函数,它在0附近的梯度是最大的,这样就有利于在反向传播时加速收敛,同时也能避免sigmoid的梯度消失的问题),这样就能加速模型的收敛了。
但是又出现了一个新的问题,也就是如果我们输入激活函数的分布是均值为0,方差为单位方差的正太分布,打个比方还是sigmoid函数,我们一直利用到的是0附近的线性区域,也就是说我们的非线性函数和线性函数的效果相同了?!那我们的深层学习就失去了意义,因为它相当于变成了一个多层的线性变换!这和一层的线性网络是等价的,网络的非线性表达能力下降了。
于是BN的作者为了满足网络能够学习非线性的能力,对进行了正太分布变换的数据,又添加一个scale和shift操作。
y=scale*x+shift
这个操作使数据在中心区域附近的线性区域往旁边的非线性区域动了动,这两个参数的核心思想就是兼顾线性的快速收敛,与非线性的较强表达能力。这两个参数需要进行设置。
Batch Normalization的过程
论文算法流程:
需要提到的是,在训练过程使用的是Mini Batch Gradient Descent。里面的均值和方差是每一个batch的均值方差。批量梯度下降针对随机梯度下降(只采用一个样本)的优点也能够在Batch Normalization得到体现。关于这两种梯度下降,在这篇文章提到了更多的细节。
小结
BatchNormalization的优点:
- BN对每一批数据进行归一化到一个相同的分布,而每一批数据的均值和方差会有一定差别,而不是固定的值,这个差别实际上能够增加模型的鲁棒性,在一定程度上减少过拟合
- 提升训练速度,加速模型的收敛
- 可以有效缓解Relu的Dead问题,使用较大的学习率