priority_queue的使用

priority_queue的介绍

 priority_queue文档介绍

优先级队列默认使用vector作为其底层存储数据的容器，在vector上又使用了堆算法将vector中的元素构造成堆的结构，因此priority_queue就是堆，所有需要用到堆的位置，都可以考虑使用priority_queue。

注意： 默认情况下priority_queue是大堆。

priority_queue的定义方式

方式一： 使用vector作为底层容器，内部构造大堆结构。

priority_queue<int, vector<int>, less<int>> q1;

方式二： 使用vector作为底层容器，内部构造小堆结构。

priority_queue<int, vector<int>, greater<int>> q2;

方式三： 不指定底层容器和内部需要构造的堆结构。

priority_queue<int> q;

注意： 此时默认使用vector作为底层容器，内部默认构造大堆结构。

priority_queue各个接口的使用

成员函数	功能
empty	判断队列是否为空
size	获取队列中有效元素个数
top	访问队头元素（堆顶元素）
push	插入元素到队尾（并排序）
pop	弹出队头元素（堆顶元素）
swap	交换两个队列中的数据

示例：

#include <iostream>
#include <functional>
#include <queue>
using namespace std;
int main()
{priority_queue<int> q;//默认使用vector作为底层容器，默认构造大堆结构//进行插入数据时，会自动进行排序，构成堆结构q.push(3);q.push(6);q.push(0);q.push(2);q.push(9);q.push(8);q.push(1);while (!q.empty()){cout << q.top() << " ";q.pop();}cout << endl; //9 8 6 3 2 1 0return 0;
}

如果在priority_queue中放自定义类型的数据，用户需要在自定义类型中提供> 或者< 的重载

class Date
{
public:Date(int year = 1900, int month = 1, int day = 1): _year(year), _month(month), _day(day){}bool operator<(const Date& d)const{return (_year < d._year) ||(_year == d._year && _month < d._month) ||(_year == d._year && _month == d._month && _day < d._day);}bool operator>(const Date& d)const{return (_year > d._year) ||(_year == d._year && _month > d._month) ||(_year == d._year && _month == d._month && _day > d._day);}friend ostream& operator<<(ostream& _cout, const Date& d){_cout << d._year << "-" << d._month << "-" << d._day;return _cout;}
private:int _year;int _month;int _day;
};
void TestPriorityQueue()
{// 大堆，需要用户在自定义类型中提供<的重载priority_queue<Date> q1;q1.push(Date(2018, 10, 29));q1.push(Date(2018, 10, 28));q1.push(Date(2018, 10, 30));cout << q1.top() << endl;// 如果要创建小堆，需要用户提供>的重载priority_queue<Date, vector<Date>, greater<Date>> q2;q2.push(Date(2018, 10, 29));q2.push(Date(2018, 10, 28));q2.push(Date(2018, 10, 30));cout << q2.top() << endl;
}

仿函数

代码样例

仿函数相当于一个类对象，通常使用它的时候要求重载一个运算符 —— 括号运算符【operator()】

如果是比较仿函数，返回默认值，所以我们通常使用bool

bool operator()() 

为了让仿函数使用更广泛，可将其变为模板

下面代码就实现了 x 和 y 的比较

为了与库区别开来，创造一个命名空间存放比较仿函数

#include<iostream>
using namespace std;// 仿函数/函数对象
namespace wyt
{template<class T>class less{public:bool operator()(const T& x, const T& y) const{return x < y;}};template<class T>class greater{public:bool operator()(const T& x, const T& y) const{return x > y;}};
}

使用场景（示例）

1.简单应用

仿函数的对象可以像函数一样使用，因此被称为仿函数

int main()
{wyt::less<int> lessFunc;lessFunc(1, 2);    //等价于下方的运算符重载//lessFunc.operator()(1, 2);
}

2.冒泡排序

添加一个额外的模板Compare，在函数中创建一个Compare的对象com，使代码运行时能进行推演。

namespace wyt
{template<class T>class less{public:bool operator()(const T& x, const T& y) const{return x < y;}};template<class T>class greater{public:bool operator()(const T& x, const T& y) const{return x > y;}};
}template<class T, class Compare>
//void BubbleSort(T* a, int n, const Compare& com) - 没有成员变量的类只有1个字节，拷贝代价不大，因此可以不用&
void BubbleSort(T* a, int n, Compare com)
{for (int j = 0; j < n; ++j){int exchange = 0;for (int i = 1; i < n - j; ++i){//if (a[i] < a[i - 1])if (com(a[i], a[i - 1])){swap(a[i - 1], a[i]);exchange = 1;}}if (exchange == 0){break;}}
}

测试用例

int main()
{wyt::less<int> lessFunc;//<wyt::greater<int> greaterFunc;//>int a[] = { 2, 3, 4, 5, 6, 1, 2, 4, 9 };//升序//BubbleSort(a, sizeof(a) / sizeof(int), lessFunc); - lessFunc有名对象BubbleSort(a, sizeof(a) / sizeof(int), wyt::less<int>()); //wyt::less<int>()匿名对象for (auto e : a){cout << e << " ";}cout << endl;//降序BubbleSort(a, sizeof(a) / sizeof(int), greaterFunc);for (auto e : a){cout << e << " ";}cout << endl;return 0;
}

priority_queue的模拟实现

priority_queue的底层实际上就是堆结构，实现priority_queue之前，我们先认识两个重要的堆算法。（下面这两种算法我们均以大堆为例）

堆的向上调整算法

以大堆为例，堆的向上调整算法就是在大堆的末尾插入一个数据后，经过一系列的调整，使其仍然是一个大堆。

调整的基本思想如下：
1、将目标结点与其父结点进行比较。
2、若目标结点的值比父结点的值大，则交换目标结点与其父结点的位置，并将原目标结点的父结点当作新的目标结点继续进行向上调整；若目标结点的值比其父结点的值小，则停止向上调整，此时该树已经是大堆了。

例如，现在我们在该大堆的末尾插入数据88。

我们先将88与其父结点55进行比较，发现88比其父结点大，则交换父子结点的数据，并继续进行向上调整。

此时将88与其父结点80进行比较，发现88还是比其父结点大，则继续交换父子结点的数据，并继续进行向上调整。

这时再将88与其父结点99进行比较，发现88比其父结点小，则停止向上调整，此时该树已经就是大堆了。

堆的向上调整算法代码：

//堆的向上调整（大堆）
void AdjustUp(vector<int>& v, int child)
{int parent = (child - 1) / 2; //通过child计算parent的下标while (child > 0)//调整到根结点的位置截止{if (v[parent] < v[child])//孩子结点的值大于父结点的值{//将父结点与孩子结点交换swap(v[child], v[parent]);//继续向上进行调整child = parent;parent = (child - 1) / 2;}else//已成堆{break;}}
}

堆的向下调整算法

以大堆为例，使用堆的向下调整算法有一个前提，就是待向下调整的结点的左子树和右子树必须都为大堆。

调整的基本思想如下：
1、将目标结点与其较大的子结点进行比较。
2、若目标结点的值比其较大的子结点的值小，则交换目标结点与其较大的子结点的位置，并将原目标结点的较大子结点当作新的目标结点继续进行向下调整；若目标结点的值比其较大子结点的值大，则停止向下调整，此时该树已经是大堆了。

例如，将该二叉树从根结点开始进行向下调整。（此时根结点的左右子树已经是大堆）

将65与其较大的子结点88进行比较，发现60比其较大的子结点小，则交换这两个结点的数据，并继续进行向下调整.

此时再将65与其较大的子结点80进行比较，发现60比其较大的子结点小，则再交换这两个结点的数据，并继续进行向下调整。

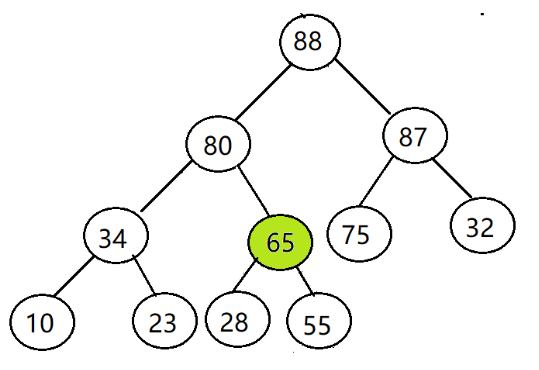
这时再将65与其较大的子结点55进行比较，发现65比其较大的子结点大，则停止向下调整，此时该树已经就是大堆了。

堆的向下调整算法代码：

//堆的向下调整（大堆）
void AdjustDown(vector<int>& v, int n, int parent)//n是节点个数
{//child记录左右孩子中值较大的孩子的下标int child = 2 * parent + 1;//先默认其左孩子的值较大while (child < n){if (child + 1 < n&&v[child] < v[child + 1])//右孩子存在并且右孩子比左孩子还大{child++;//较大的孩子改为右孩子}if (v[parent] < v[child])//左右孩子中较大孩子的值比父结点还大{//将父结点与较小的子结点交换swap(v[child], v[parent]);//继续向下进行调整parent = child;child = 2 * parent + 1;}else//已成堆{break;}}
}

priority_queue的模拟实现

只要知道了堆的向上调整算法和堆的向下调整算法，priority_queue的模拟实现就没什么困难了。

成员函数	实现方法
empty	判断容器是否为空
size	返回容器的当前大小
top	返回容器的第0个元素
push	在容器尾部插入元素后进行一次向上调整算法
pop	将容器头部和尾部元素交换，再将尾部元素删除，最后从根结点开始进行一次向下调整算法

priority_queue模拟实现代码：

namespace wyt //防止命名冲突
{//比较方式（使内部结构为大堆）template<class T>struct less{bool operator()(const T& x, const T& y){return x < y;}};//比较方式（使内部结构为小堆）template<class T>struct greater{bool operator()(const T& x, const T& y){return x > y;}};//优先级队列的模拟实现template<class T, class Container = vector<T>, class Compare = less<T>>//默认是大堆class priority_queue{public:priority_queue(){}template <class InputIterator>         priority_queue(InputIterator first, InputIterator last):_con(first, last){// 向下调整建堆 -- 将容器内的数据建成堆结构for (int i = (_con.size() - 1 - 1) / 2; i >= 0; --i){AdjustDown(i);}}//堆的向上调整void AdjustUp(size_t child){size_t parent = (child - 1) / 2; //通过child计算parent的下标while (child > 0)//调整到根结点的位置截止{if (_com(_con[parent], _con[child]))//通过所给比较方式确定是否需要交换结点位置{//将父结点与孩子结点交换swap(_con[child], _con[parent]);//继续向上进行调整child = parent;parent = (child - 1) / 2;}else//已成堆{break;}}}//插入元素到队尾（并排序）void push(const T& x){_con.push_back(x);AdjustUp(_con.size() - 1); //将最后一个元素进行一次向上调整}//堆的向下调整void AdjustDown(size_t parent){size_t child = 2 * parent + 1;while (chile < _con.size()){//if (child+1 < _con.size() && _con[child] < _con[child+1])if (child + 1 < _con.size() && com(_con[child], _con[child + 1])){child++;}//if (_con[parent] < _con[child])if (com(_con[parent], _con[child])){swap(_con[child], _con[parent]);parent = child;child = parent * 2 + 1;}else{break;}}}//弹出队头元素（堆顶元素）void pop(){swap(_con[0], _con[_con.size() - 1]);_con.pop_back();AdjustDown(0); //将第0个元素进行一次向下调整}//访问队头元素（堆顶元素）T& top(){return _con[0];}const T& top() const{return _con[0];}//获取队列中有效元素个数size_t size() const{return _con.size();}//判断队列是否为空bool empty() const{return _con.empty();}private:Container _con; //底层容器Compare _com; //比较方式};
}

总结

以上就是priority_queue的使用与模拟实现，其中关于堆的知识，我们在数据结构二叉树中也讲解过，点击此处进行查看