（一）去空间不变的模糊核

1）维纳滤波

一个理想点经过相机后成的像由点扩散函数PSF(Point Spread Function)来描述。
线性移不变的PSF导致的图像模糊：b=c*x+n n是噪声 例如衍射极限PSF 相机抖动模糊

直接去卷积会放大系统中高频部分的的噪声
维纳滤波：把图像和噪声都看做是随机过程，并把去卷积的问题看作是一个最大似然问题去求解。

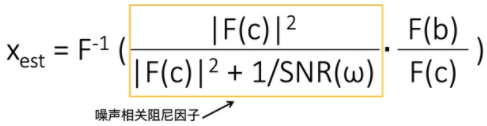
SNR(ω)是频率ω的信噪比
当噪声很低时，SNR(ω)很高，上式接近于去卷积 。
而当噪声较大时，则上式接近于0。
实际上，对于自然图像，一般认为其功率谱与1/ww 线性相关，同时我们认为噪声是白噪声，其功率是与频率无关的常量
那么一般SNR(ω)=1/ww

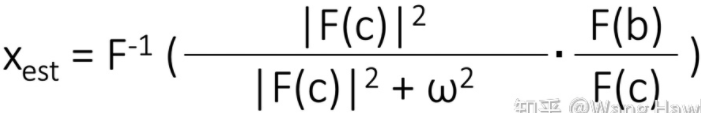
也可以理解为

2）Richardson-Lucy方法

通过迭代的方式得到去卷积结果

3）盲去卷积（卷积核未知）

https://zhuanlan.zhihu.com/p/105500403
可以假设噪声是均值为0的高斯噪声。
先用部分图像块估算卷积核K（变分贝叶斯）， 拟合图像的梯度分布（重尾分布）
再用Richardson-Lucy算法进行去卷积

High-quality Motion Deblurring from a Single Image 改进
假设噪声满足高斯分布–>>更复杂的噪声模型，噪声的概率分布由其0阶、1阶、2阶梯度的分布来描述
用混合高斯模型来拟合重尾模型–>>更简单的拟合重尾分布的函数
用混合指数分布来描述模糊核的形态–>>加入了局部平滑区域的约束，避免出现振铃效应
采用RL算法去卷积–>>复杂的优化方法，交替式的优化估计清晰图像L和模糊核K

（二）失焦模糊：

镜头是有景深的，因此景深范围内的物体可以清晰成像，不在这个范围内的物体则会显得模糊。
失焦模糊对画面中每个点都不一致的。各个失焦距离的PSF构成失焦簇
失焦的PSF其实和镜头的光圈形状高度相关，因此，失焦的PSF相对更加容易测量一些


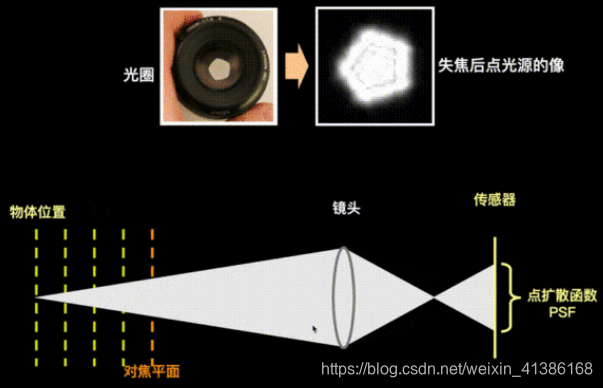
当镜头的像距、焦距固定好后，对焦平面也固定了。
提前获取到失焦的图像x和清晰的图像b，可以反向去卷积得到卷积核c。
当然实际操作时，通常还需要加入一定的正则化，来限制卷积核中的噪声。

Image and depth from a conventional camera with a coded aperture
自然图像的特殊之处就是其梯度是稀疏的，因此可以用正则项惩罚梯度项，防止振铃


难点：
即便知道了接近正确的卷积核的尺寸和形状，对应失焦类型的卷积核，也很难通过传统的去卷积方法得到清晰的图像。比如采用经典的Richardson-Lucy方法处理失焦图像很多时候会产生强烈的振铃效应：
用不同尺度的卷积核去卷积后，很多时候很难分清楚哪个更清晰, 特别是比正确尺寸略小的卷积核的去卷积结果很难和正确尺寸的结果相区分， 这导致我们很难为每个区域都选择出正确的卷积核。

（三）运动模糊

快门速度不够快时，拍摄的图像会模糊、拖尾，这种模糊我们称之为“运动模糊”

生成方法：
1）时间反失真
高帧率多帧积累渲染的到低帧频。
2）设定角度距离，对目标进行叠加

难点：
很难获取到准确的卷积核，因为卷积核跟物体的远近、物体运动的速度方向都有关系。
场景中的各个物体有不同的运动方向和速度，还可能有固定的背景，所以需要把需要恢复的物体分割开来。
运动卷积核丢失了高频信息，去卷积技术就会面临严重的信噪比低的问题。

水平一维运动物体的运动模糊相当于一个一维的Box Filter，这个卷积核的傅里叶变换是一个Sinc函数，有大量接近零的点，导致去卷积时出现大量的噪声，最终结果信噪比极低。这时的运动模糊使得很多频域信息损失掉了，无法准确恢复出原始信号。

去模糊论文整理： https://github.com/subeeshvasu/Awesome-Deblurring