集成学习

refs

• 1.11. 集成方法 - sklearn (scikitlearn.com.cn)

• 1.11. Ensemble methods — scikit-learn documentation

• 西瓜书|机器学习|周

摘要

• 集成学习(ensemble learning)通过构建并结合多个学习器来完成学习任务，有时也被称为多分类器系统(multi-classifier system)、基于委员会的学习(committee-based learning)等.

• 集成学习的一般结构:先产生一组“个体学习器”(individual learner)，再用某种策略将它们结合起来.

  • 个体学习器通常由一个现有的学习算法从训练数据产生,例如决策树算法、BP神经网络算法等,此时集成中只包含同种类型的个体学习器
  • 例如“决策树集成”中全是决策树，“神经网络集成”中全是神经网络,这样的集成是“同质”的(homogeneous)．
  • 同质集成中的个体学习器亦称“基学习器”(base learner),相应的学习算法称为“基学习算法”(base learning algorithm).
  • 集成也可包含不同类型的个体学习器,例如同时包含决策树和神经网络,这样的集成是“异质”的(heterogenous).
  • 异质集成中的个体学习器由不同的学习算法生成,这时就不再有基学习算法;
  • 相应的,个体学习器一般不称为基学习器,常称为“组件学习器”(component learner)或直接称为个体学习器.

• 集成学习通过将多个学习器进行结合,常可获得比单一学习器显著优越的泛化性能.

  • 这对“弱学习器”(weak learner)尤为明显,因此集成学习的很多理论研究都是针对弱学习器进行的,
  • 基学习器有时也被直接称为弱学习器

• 但需注意的是,虽然从理论上来说使用弱学习器集成足以获得好的性能,但在实践中出于种种考虑，例如希望使用较少的个体学习器,或是重用关于常见学习器的一些经验等，人们往往会使用比较强的学习器.

• 在一般经验中,如果把好坏不等的东西掺到一起,那么通常结果会是比最坏的要好一些,比最好的要坏一些.

  • 集成学习把多个学习器结合起来,如何能获得比最好的单一学习器更好的性能呢?

• 考虑一个简单的例子:在二分类任务中,假定三个分类器在三个测试样本上的表现:

  • 
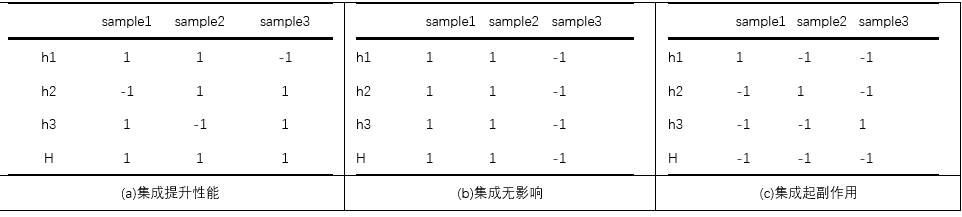
  • 其中1表示对应的分类器分类正确,-1表示分类错误,其中$h_i$表示第$i$个’个体学习器’,H表示对个体学习器的集成
  • 集成学习的结果通过投票法(voting)产生,即“少数服从多数”.
  • 在(a)中,每个分类器都只有66.6%的精度,但集成学习却达到了100%;
  • 在(b)中,三个分类器没有差别,集成之后性能没有提高,依然为66.6%;
  • 在©中，每个分类器的精度都只有33.3%，集成学习的结果变得更糟.

• 综上:要获得好的集成,个体学习器应“好而不同”

  • 个体学习器要有一定的“准确性(accuracy)”，即学习器于不能太坏,
  • 并且要有“多样性”(diversity)，即学习器间具有差异.

• 以二分类为例分析:

  • 设 y ∈ { − 1 , + 1 } y\in\{-1,+1\} y∈{−1,+1},真实函数$f$,假定个体分类器的错误率为$ϵ$,对于每个基分类器$h_i$:

    • $$P(h_i(\mathbf{x})\ne f(\mathbf{x}))=ϵ$$

  • 假设集成是通过简单投票法结合T个基分类器,若有超过半数的基分类器预测结果是对的,那么集成分类器对样本的预测也会是对的:

    • $$H(\mathbf{x})=\text{sign}\left(\sum _{i=1}^T{h}_i(\mathbf{x})\right)$$

    • 其中,如果$h_i$对样本$\mathbf{x}$的预测是正确的,则$h_i(\mathbf{x})=1$,否则取$-1$

    • 因此如果超过半数基分类器是正确的,那么${\sum }_{i=1}^T{h}_i(\mathbf{x})>0$从而$H(\mathbf{x})=+1$即,H的预测正确

Note

• 如果理想的假设$h_i$的错误率相互独立,根据Hoeffding不等式,集成H的错误率:

  • $$P(H(x)\ne f(x))=\sum _{k=0}^{\lfloor T/2\rfloor }\left(\genfrac{}{}{0ex}{}{T}{k}\right)(1-ϵ{)}^k{ϵ}^{T-k}⩽\exp \left(-\frac{1}{2}T(1-2ϵ{)}^2\right)$$

  • 随着T的增大,H的错误率将指数级下降,最终趋于0

  • 上面的分析有一个关键假设:基学习器的误差相互独立.

• 在现实任务中,个体学习器是为解决同一个问题训练出来的,它们显然不可能相互独立

准确性和多样性

• 个体学习器的“准确性”和“多样性”本身就存在冲突,一般的
  • 准确性很高之后，要增加多样性就需牺牲准确性.
• 如何产生并结合“好而不同”的个体学习器，是集成学习研究的核心.

集成学习方法分类

• 根据个体学习器的生成方式，目前的集成学习方法大致可分为两大类
  • 个体学习器间存在强依赖关系、必须串行生成的序列化方法，代表是Boosting,
  • 个体学习器间不存在强依赖关系、可同时生成的并行化方法,代表是Bagging和“随机森林”(Random Forest).

Boosting

• Boosting是一族可以将弱学习器提升为强学习器的算法.
• 工作机制:
  • 先从初始训练集(设分布为D)训练出一个基学习器$h_1$
  • 根据基学习器$h_1$的表现对训练样本分布进行调整(新分布$D_1$),使得先前基学习器($h_1$)做错的训练样本在后续受到更多关注
  • 基于调整后的样本分布$D_1$来训练下一个基学习器
  • 反复进行,指导基学习器数量达到事先指定的值T
  • 对T个基学习器进行加权结合

AdaBoost

• AdaBoost是Boosting族算法的著名代表。

  • AdaBoost为英文"Adaptive Boosting"（自适应增强）的缩写。
  • AdaBoost方法的自适应在于：前一个分类器分错的样本会被用来训练下一个分类器。
  • 虽然AdaBoost方法对于噪声数据和异常数据很敏感。但在一些问题中，AdaBoost方法相对于大多数其它学习算法而言，不会很容易出现过拟合现象。
  • AdaBoost方法中使用的分类器可能很弱（比如出现很大错误率），
    • 只要它的分类效果比随机好一点（比如两类问题分类错误率略小于0.5），就能够改善最终得到的模型。
    • 错误率高于随机分类器(对于一个分类问题，随机猜测答案的分类器)的弱分类器也是有用的，因为在最终得到的多个分类器的线性组合中，可以给它们赋予负系数，同样也能提升分类效果。
  • AdaBoost方法是一种迭代算法，在每一轮中加入一个新的弱分类器，直到达到某个预定的足够小的错误率。
    • 每一个训练样本都被赋予一个权重，表明它被某个分类器选入训练集的概率。
      • 如果某个样本点已经被准确地分类，那么在构造下一个训练集中，它被选中的概率就被降低；
      • 相反，如果某个样本点没有被准确地分类，那么它的权重就得到提高。
    • 通过这样的方式，AdaBoost方法能“聚焦于”那些较难分（更富信息）的样本上。
    • 在具体实现上，
      • 最初令每个样本的权重都相等。
      • 对于第k次迭代操作，我们就根据这些权重来选取样本点，进而训练分类器$C_k$。然后就根据这个分类器，来提高被它分错的的样本的权重，并降低被正确分类的样本权重。
      • 然后，权重更新过的样本集被用于训练下一个分类器。
      • 整个训练过程如此迭代地进行下去。

• 设 y i ∈ { − 1 , 1 } y_i\in\{-1,1\} yi​∈{−1,1},$f$为真实函数:

  • 加性模型(additive model):基学习器的线性组合,一种易于理解的AdaBoost推导方式:

  • $$H(\mathbf{x})=\sum _{t=1}^T{\alpha }_t{h}_t(\mathbf{x})$$

• $H(\mathbf{x})$来最小化指数损失函数(exponential loss function)

  • $$L_{exp}(H|D)=E_{\mathbf{x}\sim D}[\exp (-f(\mathbf{x})H(\mathbf{x}))]$$

伪代码

• input

  • 训练集$D=\{({\mathbf{x}}_1,y_1),({\mathbf{x}}_2,y_2),\cdots ,({\mathbf{x}}_m,y_m)\}$
  • 及学习算法$\mathfrak{L}$
  • 训练轮数$T$

• $$\begin{array}{l}\text{ 1: }{\mathcal{D}}_1(\mathbf{x})=1/m\text{. }\\ \text{ 2: }\text{for }t=1,2,\dots ,T\text{ do }\\ \text{ 3: }{h}_t=\mathfrak{L}\left(D,{\mathcal{D}}_t\right)\text{; }\\ \text{ 4: }{ϵ}_t=P_{\mathbf{x}\sim {\mathcal{D}}_t}\left(h_t(\mathbf{x})\ne f(\mathbf{x})\right)\text{; }\\ \text{ 5: }\text{ if }{ϵ}_t>0.5\text{ then break }\\ \text{ 6: }{\alpha }_t=\frac{1}{2}\ln \left(\frac{1-{ϵ}_t}{{ϵ}_t}\right)\text{; }\\ \begin{array}{lc}\text{ 7: }{\mathcal{D}}_{t+1}(\mathbf{x})& =\frac{{\mathcal{D}}_t(\mathbf{x})}{Z_t}\times \{\begin{array}{ll}\exp \left(-{\alpha }_t\right),& \text{ if }{h}_t(\mathbf{x})=f(\mathbf{x})\\ \exp \left({\alpha }_t\right),& \text{ if }{h}_t(\mathbf{x})\ne f(\mathbf{x})\end{array}\\ & =\frac{{\mathcal{D}}_t(\mathbf{x})\exp \left(-{\alpha }_{t}f(\mathbf{x})h_t(\mathbf{x})\right)}{Z_t}\end{array}\\ 8:\text{end for}\end{array}$$

• output:

  • $$H(\mathbf{x})=\mathrm{sign}\left(\sum _{t=1}^T{\alpha }_t{h}_t(\mathbf{x})\right)$$

• comments:

  • 1:初始化样本权值分布为$\frac{1}{m}$
  • 3:基于分布${\mathcal{D}}_t$从数据集D中训练出来的分类器$h_t$
  • 4:估计$h_t$的误差${ϵ}_t$
  • 6:确定分类器$h_t$的权重
  • 7:更新样本分布,$Z_t$是规范化因子,确保${\mathcal{D}}_{t+1}$是一个分布
  • 上述算法中用到的几个公式的推导较为复杂,可参考相关资料文献(西瓜书给出的推导是:基于加性模型迭代式优化指数损失函数的角度进行推导)

Adaboost小结

• AdaBoost（Adaptive Boosting）算法是一种集成学习方法，它通过结合多个弱学习器来构建一个强学习器。AdaBoost的核心思想是在每轮迭代中，根据前一轮的预测错误调整样本权重和弱学习器权重，得后续的弱学习器更关注那些被前一轮弱学习器错误分类的样本。最后，将所有弱学习器的预测结果加权结合，得到终的预测结果。

  AdaBoost算法的主要步骤如下：

  1. 初始化样本权重：将训练集中每个样本的权重设置为相等的值，即1/N，其中N是训练集的样本数量。
  2. 对于每一轮迭代： a. 使用带重的训练集训练一个弱学习器。 b. 计算弱学习器在训练集上的分类错误率。 c. 计算弱习器的权重，该权重与弱学习器的分类错误率成反比。 d. 更新样本权重：增加被错误分类样本的权重，减少正确分类样本的权重。 e. 对样本权重进行归一化，使其总和为1。
  3. 将所有弱学器的预测结果加权结合，得到最终的预测结果。

  AdaBoost算法的优点：

  1. 易实现：AdaBoost算法实现相对简单，只需在每轮迭代中调整样本权重和弱学习器权重即可。
  2. 自适应性：AdaBoost算法能够自适应地调整样本权重，使得后续的弱学习器更加关注那些被前一轮弱学习器错误分类的本。
  3. 防止过拟合：通过结合多个弱学习器，AdaBoost算法可以降低型的方差，从而减少过合的风险。

  AdaBoost算法的缺点：

  1. 对噪声数据和异常值敏感：由于AdaBoost算法会增加被错误分类样本的权重，因此对噪声数据和异常值较为敏感，可能导致模型性能下降。
  2. 顺序训练：由AdaBoost算法是一个迭代过程，每一轮训练都依赖于前一轮的结果，因此无法并行训练弱学习器，训练速度可能较慢。

补充

补充1

• Boosting 算法要求基学习器能对特定的数据分布进行学习,这可通过“重赋权法”(re-weighting)实施,即在训练过程的每一轮中,根据样本分布为每个训练样本重新赋予一个权重．
• 对无法接受带权样本的基学习算法，则可通过“重采样法”(re-sampling)来处理，即在每一轮学习中,根据样本分布对训练集重新进行采样,再用重采样而得的样本集对基学习器进行训练.
• 一般而言,这两种做法没有显著的优劣差别.
• 需注意的是,Boosting 算法在训练的每一轮都要检查当前生成的基学习器是否满足基本条件
  • (算法伪代码第5行,检查当前基分类器是否是比随机猜测好)，一旦条件不满足,则当前基学习器即被抛弃,且学习过程停止.
  • 在此种情形下,初始设置的学习轮数T也许还远未达到,可能导致最终集成中只包含很少的基学习器而性能不佳.
• 若采用“重采样法”,则可获得“重启动”机会以避免训练过程过早停止[Kohavi and Wolpert,1996],即在抛弃不满足条件的当前基学习器之后,可根据当前分布重新对训练样本进行采样,再基于新的采样结果重新训练出基学习器,从而使得学习过程可以持续到预设的T轮完成.
• 从偏差-方差分解的角度看，Boosting主要关注降低偏差,因此Boosting对能基于泛化性能相当弱的学习器构建出很强的集成．

补充2

• Boosting是一种集成学习方法，它通过结合多个弱学习器来构建一个强学习器。Boosting的核心思想是在每一轮迭代中，根据前一轮的预测错误调整样本权重，使得后续的弱学习器更加关注那些被前一轮弱学习器错误分类的样本。最后，将所有弱学习器的预测结果加权结合，得到最终的预测结果。

  Boosting方法的主要特点如下：

  1. 顺序训练：Boosting方法是一个迭代过程，每一轮训练都依赖于前一轮的结果。因此，Boosting方法无法并行训练弱学习器。
  2. 误差修正：Boosting方法通过调整样本权重，使得后续的弱学习器更加关注那些被前一轮弱学习器错误分类的样本。这有助于提高模型在复杂数据集上的性能。
  3. 防止过拟合：Boosting方法通过结合多个弱学习器来降低模型的方差，从而减少过拟合的风险。然而，如果迭代次数过多，Boosting方法仍然可能导致过拟合。

• Boosting方法的常见算法包括：

  • AdaBoost（Adaptive Boosting）：AdaBoost是最早的Boosting算法之一，它通过调整样本权重和弱学习器权重来实现误差修正。在每一轮迭代中，AdaBoost会增加被错误分类样本的权重，同时减少正确分类样本的权重。弱学习器的权重与其在训练集上的分类准确率有关。
  • Gradient Boosting：Gradient Boosting是一种通用的Boosting算法，它通过优化损失函数的梯度来实现误差修正。在每一轮迭代中，Gradient Boosting会训练一个新的弱学习器来拟合前一轮预测结果与真实标签之间的残差。最后，将所有弱学习器的预测结果累加，得到最终的预测结果。
    • XGBoost（eXtreme Gradient Boosting）：XGBoost是Gradient Boosting的一种优化实现，它在原始的Gradient Boosting算法基础上引入了正则化项，以防止过拟合。
    • 此外，XGBoost还采用了一些高效的计算技术，如列块存储、缓存感知访问模式和并行计算，以提高训练速度。

• 总之，Boosting是一种集成学习方法，它通过结合多个弱学习器来构建一个强学习器。Boosting方法的核心思想是在每一轮迭代中，根据前一轮的预测错误调整样本权重，使得后续的弱学习器更加关注那些被前一轮弱学习器错误分类的样本。

Bagging

• 欲得到泛化性能强的集成,集成中的个体学习器应尽可能相互独立;
• 虽然“独立”在现实任务中无法做到,但可以设法使基学习器尽可能具有较大的差异给定一个训练数据集
  • 一种可能的做法是对训练样本进行采样,产生出若干个不同的子集,再从每个数据子集中训练出一个基学习器，这样，由于训练数据不同,我们获得的基学习器可望具有比较大的差异
  • 同时我们还希望个体学习器不能太差
    • 如果采样出的每个子集都完全不同,则每个基学习器只用到了一小部分训练数据，甚至不足以进行有效学习,这显然无法确保产生出比较好的基学习器.
    • 为解决这个问题,我们可考虑使用相互有交叠的采样子集.

Bagging

• Bagging (Bootstrap Aggereating的缩写)[Breiman,1996a]是并行式集成学习方法最著名的代表.

• Bagging 的基本流程:

  • 它直接基于自助采样法(bootstrap sampling).给定包含m个样本的数据集,我们先随机取出一个样本放入采样集中,再把该样本放回初始数据集,使得下次采样时该样本仍有可能被选中,这样,经过m次随机采样操作，我们得到含m个样本的采样集,初始训练集中有的样本在采样集里多次出现,有的则从未出现.(根据统计规律求极限(m足够大时)可知初始训练集中约有63.2%的样本出现在采样集中.)

  • 我们可采样出T个含m个训练样本的采样集,然后基于每个采样集训练出一个基学习器,再将这些基学习器进行结合.

• 对预测输出进行结合,Bagging 通常

  • 对分类任务使用简单投票法,
  • 对回归任务使用简单平均法
    • 若分类预测时出现两个类收到同样票数的情形，则最简单的做法是随机选择一个
    • 也可进一步考察学习器投票的置信度来确定最终胜者.
  • Note:每个基学习器使用相同的权重和平均

伪代码

• Bagging的算法描述(伪代码)

• input:

  • 训练集$D=\{({\mathbf{x}}_1,y_1),({\mathbf{x}}_2,y_2),\cdots ,({\mathbf{x}}_m,y_m)\}$;
  • 及学习算法$\mathfrak{L}$
  • 训练轮数$T$

• $$\begin{array}{lc}\text{1:}& \text{for}t=1,2,\cdots ,T\text{do}\\ \text{2:}& h_t=\mathfrak{L}(D,{\mathcal{D}}_{bs})\\ \text{3:}& \text{end for}\end{array}$$

• output:

  • $$H(\mathbf{x})=\underset{y\in \gamma }{\mathrm{argmax}}\sum _{t=1}^T\mathbb{I}(h_t(\mathbf{x})=y)$$

特点

算法效率

• 假定基学习器的计算复杂度为$O(m)$，则 Bagging 的复杂度大致为$T(O(m)＋O(s))$，考虑到采样与投票/平均过程的复杂度$O(s)$很小，而$T$通常是一个不太大的常数,因此,训练一个Bagging集成与直接使用基学习算法训练一个学习器的复杂度同阶,这说明Bagging是一个很高效的集成学习算法.

直接应用于多分类

• 与标准AdaBoost 只适用于二分类任务不同,Bagging 能不经修改地用于多分类、回归等任务.

自助采样和包外估计

• 自助采样过程还给Bagging 带来了另一个优点:由于每个基学习器只使用了初始训练集中约63.2%的样本,剩下约36.8%的样本可用作验证集来对泛化性能进行包外估计(out-of-bag estimate,oob)[Breiman，1996a;Wolpert and Macready,1999].

• 为此需记录每个基学习器所使用的训练样本.

  • 不妨令$D_t$表示$h_t$ 实际使用的训练样本集

  • 令$H^{oob}(\mathbf{x})$表示对样本$\mathbf{x}$ 的包外预测,即仅考虑那些未使用$\mathbf{x}$训练的基学习器在$\mathbf{x}$上的预测,有

    • $$H^{oob}(\mathbf{x})=\underset{y\in \gamma }{\mathrm{argmax}}\sum _{t=1}^T\mathbb{I}(h_t(\mathbf{x})=y)\cdot \mathbb{I}(\mathbf{x}\notin D_t)$$

  • Bagging的泛化误差的包外估计为:

    • $${ϵ}^{oob}=\frac{1}{|D|}\sum _{(\mathbf{x},y)\in D}\mathbb{I}(H^{oob}(\mathbf{x})\ne y)$$

• 事实上,包外样本还有许多其他用途

  • 例如当基学习器是决策树时,可使用包外样本来辅助剪枝,或用于估计决策树中各结点的后验概率以辅助对零训练样本结点的处理;
  • 当基学习器是神经网络时,可使用包外样本来辅助早期停止以减小过拟合风险.

• 从偏差-方差分解的角度看，Bagging主要关注降低方差,因此它在不剪枝决策树、神经网络等易受样本扰动的学习器上效用更为明显.

随机森林

• 随机森林(Random Forest，简称RF) [Breiman，2001a]是 Bagging 的一个扩展变体.
• RF在以决策树为基学习器构建Bagging 集成的基础上，进一步在决策树的训练过程中引入了随机属性选择.
• 传统决策树在选择划分属性时是在当前结点的属性集合(假定有d个属性)中选择一个最优属性;
• 而在RF中,对基决策树的每个结点,先从该结点的属性集合中随机选择一个包含k个属性的子集,然后再从这个子集中选择一个最优属性用于划分.
• 这里的参数k控制了随机性的引入程度;
  • 若令k = d,则基决策树的构建与传统决策树相同;
  • 若令k= 1，则是随机选择一个属性用于划分;
  • 一般情况下,推荐值$k={\log }_{2}d$[Breiman，2001a].
  • 随机森林简单、容易实现、计算开销小,它在很多现实任务中展现出强大的性能,被誉为“代表集成学习技术水平的方法”.
• 随机森林对Bagging只做了小改动,但是与Bagging 中基学习器的“多样性”仅通过样本扰动(通过对初始训练集采样)而来不同,随机森林中基学习器的多样性不仅来自样本扰动,还来自属性扰动,这就使得最终集成的泛化性能可通过个体学习器之间差异度的增加而进一步提升.
• 随机森林的收敛性与 Bagging 相似
• 随机森林的起始性能往往相对较差,特别是在集成中只包含一个基学习器时.
  • 这很容易理解，因为通过引入属性扰动,随机森林中个体学习器的性能往往有所降低.然而,随着个体学习器数目的增加，随机森林通常会收敛到更低的泛化误差.
  • 值得一提的是,随机森林的训练效率常优于Bagging,因为在个体决策树的构建过程中，Bagging使用的是“确定型”决策树,在选择划分属性时要对结点的所有属性进行考察，而随机森林使用的“随机型”决策树则只需考察一个属性子集.

Stacking

• sklearn.ensemble.StackingClassifier — scikit-learn documentation

• <<Mastering Machine Learning with scikit-learn v2>>,简称MMLWS

sklearn中的Stacking🎈

• Stacking集成方法在0.22版本加入：Version 0.22.2.post1 — scikit-learn documentation

• Stacked generalization is a method for combining estimators to reduce their biases [W1992] [HTF]. More precisely, the predictions of each individual estimator are stacked together and used as input to a final estimator to compute the prediction. This final estimator is trained through cross-validation.

  The StackingClassifier and StackingRegressor provide such strategies which can be applied to classification and regression problems.

构造初级学习器

• The estimators parameter corresponds to the list of the estimators which are stacked together in parallel on the input data. It should be given as a list of names and estimators:

  from sklearn.linear_model import RidgeCV, LassoCV
  from sklearn.neighbors import KNeighborsRegressor
  estimators = [('ridge', RidgeCV()),('lasso', LassoCV(random_state=42)),('knr', KNeighborsRegressor(n_neighbors=20,metric='euclidean'))]
  

• 堆叠泛化（Stacked Generalization）是一种将估算器组合起来以减少其偏差的方法[W1992] [HTF]。更具体地说，将每个独立估算器的预测结果堆叠在一起，并将其用作最终估算器的输入来计算预测结果。这个最终估算器是通过交叉验证进行训练的。

  StackingClassifier和StackingRegressor提供了这样的策略，可以应用于分类和回归问题。

  estimators参数对应于在输入数据上并行堆叠在一起的估算器列表。它应该作为名称和估算器的列表给出

构造次级学习器

• The final_estimator will use the predictions of the estimators as input. It needs to be a classifier or a regressor when using StackingClassifier or StackingRegressor, respectively:

  • from sklearn.ensemble import GradientBoostingRegressor
    from sklearn.ensemble import StackingRegressor
    #定义次级学习器
    final_estimator = GradientBoostingRegressor(n_estimators=25, subsample=0.5, min_samples_leaf=25, max_features=1,random_state=42)
    #将初级学习器和次级学习器堆叠,得到一个集成的堆叠学习器
    reg = StackingRegressor(estimators=estimators,final_estimator=final_estimator)
    

• To train the estimators and final_estimator, the fit method needs to be called on the training data:

  • # 加载糖尿病数据(做回归回归任务)
    from sklearn.datasets import load_diabetes
    X, y = load_diabetes(return_X_y=True)
    #利用tts方法将数据集简单分割
    # 做基本的留出法实验
    from sklearn.model_selection import train_test_split
    X_train, X_test, y_train, y_test = train_test_split(X, y,random_state=42)
    #在训练集上训练
    reg.fit(X_train, y_train)
    

• During training, the estimators are fitted on the whole training data X_train. They will be used when calling predict or predict_proba.

• To generalize and avoid over-fitting, the final_estimator is trained on out-samples using sklearn.model_selection.cross_val_predict internally.

• For StackingClassifier, note that the output of the estimators is controlled by the parameter stack_method and it is called by each estimator. This parameter is either a string, being estimator method names, or 'auto' which will automatically identify an available method depending on the availability, tested in the order of preference: predict_proba, decision_function and predict.

• A StackingRegressor and StackingClassifier can be used as any other regressor or classifier, exposing a predict, predict_proba, and decision_function methods, e.g.:

  • y_pred = reg.predict(X_test)
    # 计算r2分数
    from sklearn.metrics import r2_score
    print('R2 score: {:.2f}'.format(r2_score(y_test, y_pred)))

• 在训练期间，估算器将在整个训练数据X_train上进行拟合。在调用predict或predict_proba时，它们将被用于预测。为了泛化和避免过度拟合，final_estimator将使用sklearn.model_selection.cross_val_predict在out-of-sample上进行训练。

  对于StackingClassifier，请注意估算器的输出由stack_method参数控制，并由每个估算器调用。该参数可以是一个字符串，即估算器方法名称，或者是“auto”，它将根据可用性自动识别一种方法，首选顺序为：predict_proba、decision_function和predict。

  StackingRegressor和StackingClassifier可以像其他回归器或分类器一样使用，暴露出predict、predict_proba和decision_function方法

多层堆叠

• Multiple stacking layers can be achieved by assigning final_estimator to a StackingClassifier or StackingRegressor:

• from sklearn.datasets import load_diabetesX, y = load_diabetes(return_X_y=True)
  from sklearn.model_selection import train_test_splitX_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)from sklearn.ensemble import (RandomForestRegressor,GradientBoostingRegressor,StackingRegressor,
  )
  from sklearn.neighbors import KNeighborsRegressor
  from sklearn.linear_model import RidgeCV, LassoCV#第一层堆叠器
  # 个体学习器rfr,gbr(# (都是集成学习器,指定较多超参数))
  final_layer_rfr = RandomForestRegressor(n_estimators=10, max_features=1, max_leaf_nodes=5, random_state=42
  )
  final_layer_gbr = GradientBoostingRegressor(n_estimators=10, max_features=1, max_leaf_nodes=5, random_state=42
  )# 第一层元学习器使用Ridge,并将第一层个体学习器共同打包为第一层堆叠器
  final_layer = StackingRegressor(estimators=[("rf", final_layer_rfr), ("gbrt", final_layer_gbr)],final_estimator=RidgeCV(),
  )
  #构建第二层堆叠器
  # 个体学习器(使用默认参数,书写更具紧凑和简洁),次级学习器使用第一层堆叠器
  multi_layer_regressor = StackingRegressor(estimators=[("ridge", RidgeCV()),("lasso", LassoCV(random_state=42)),("knr", KNeighborsRegressor(n_neighbors=20, metric="euclidean")),],final_estimator=final_layer,
  )
  # 训练这个多层堆叠回归器
  multi_layer_regressor.fit(X_train, y_train)
  # 评估分数
  print("R2 score: {:.2f}".format(multi_layer_regressor.score(X_test, y_test)))
  

Stacking特点

• In practice, a stacking predictor predicts as good as the best predictor of the base layer and even sometimes outperforms it by combining the different strengths of the these predictors.

• However, training a stacking predictor is computationally expensive.

  实际上，堆叠预测器的预测结果和基层的最佳预测器一样好，甚至有时会通过结合这些预测器的不同优点而表现更好。然而，训练堆叠预测器的计算成本很高。

StackingClassifier

• Stack of estimators with a final classifier.

  Stacked generalization consists in stacking the output of individual estimator and use a classifier to compute the final prediction. Stacking allows to use the strength of each individual estimator by using their output as input of a final estimator.

  Note that estimators_ are fitted on the full X while final_estimator_ is trained using cross-validated predictions of the base estimators using cross_val_predict.

  具有最终分类器的估计器堆栈。

  堆叠泛化的方法是将每个估计器的输出堆叠起来，并使用一个分类器来计算最终预测结果。将每个估计器的输出作为最终估计器的输入，堆叠能够利用每个估计器的优势。

  请注意，estimators_是在完整的X上拟合的，而final_estimator_是使用基估计器的交叉验证预测来训练的，使用了cross_val_predict方法。

Note

• For StackingClassifier, when using stack_method_='predict_proba', the first column is dropped when the problem is a binary classification problem. Indeed, both probability columns predicted by each estimator are perfectly collinear.

demo

1. 导入所需的库和模块：

from sklearn.datasets import load_irissklearn.ensemble import RandomForestClassifier
from sklearn.svm import LinearSVC
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import make_pipeline
from sklearn.ensemble import StackingClassifier

1. 加载鸢尾花数据集：

X, y = load_iris(return_X_y=True)

X是一个包含鸢尾花集的特征的矩阵，y是一个包含鸢尾花数据集的目标类别的向量。

• 定义基本分类器（基模型）：

  • estimators = [('rf', RandomForestClassifier(n_estimators=10, random_state=42)),('svr', make_pipeline(StandardScaler(),LinearSVC(random_state=42)))
    ]
    

  • 这里定义了两个基本分类器：一个是随机森林分类器（RandomForestClassifier），另一个是性支持向量机分类器（LinearSVC）。线性支持向量机分类器使用make_pipeline函数与StandardScaler预处理器组合，以确保在训练过程中对数据进行准化。

• 定义堆叠分类器：

  • clf = StackingClassifier(estimators=estimators, final_estimator=LogisticRegression()
    )
    

  • 堆叠分类器（StackingClassifier）使用基本分类器（estimators）和一个最终的元分类器（final_estimator）。在这个例子中元分类器是一个逻辑回归分类器（LogisticRegression）。

• 将数据集划分为训练集和测试集：

  • from sklearn.model_selection import train_test_split
    X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=42
    )
    

  • train_test_split函数将数据集划分为训练集和测试集，其中stratify=y确训练集和测试集中的类别分布与原始数据集相同。

• 训练堆叠分类器并评估其性能：

  • clf.fit(X_train, y_train).score(X_test, y_test)
    

• fit方法用于训练堆叠分类器，score方法用于估分类器在测试集上的准确性。这将返回一个介于0和1之间的分数，表示分类器在测试集上的准确性总之，这段代码实现了一个堆叠分类器，用于对鸢尾花数据集进行分类。堆叠分类器结合了多个基本分类器的预测，并使用元分类器来生成最终的预测结果。这种方法可以提高模型的性能和泛化能力。

Stacking主要内容

相关论文和术语

• 在Wolpert的论文 “Stacked generalization”（堆叠泛化）中，介绍了一种集成学习方法，即Stacking。以下是论文中的一些关键术语及其中英文对照解释：

  1. Stacked Generalization（堆叠泛化）：一种集成学习方法，通过结合多个基学习器的预测结果，生成一个新的、更强大的模型（元学习器）。
  2. Generalizer（泛化器）：在这篇论文中，泛化器是指机器学习模型，它可以是基学习器或元学习器。
  3. Level-0 Generalizer（0级泛化器）：又称为基学习器，是在训练集上训练的多个不同类型的模型。
  4. Level-1 Generalizer（1级泛化器）：又称为元学习器，是一个模型，使用基学习器生成的元特征进行训练。
  5. Meta-features（元特征）：基学习器对训练集进行预测所生成的新特征，用于训练元学习器。
  6. Cross-validation（交叉验证）：一种评估模型性能的方法，将数据集划分为K个子集，每次使用K-1个子集进行训练，剩下的子集进行验证。这个过程重复K次，每次使用不同的子集进行验证。
  7. Bias（偏差）：模型预测值与真实值之间的差异，衡量了模型的准确性。偏差较大的模型可能无法捕捉到数据中的基本关系。
  8. Variance（方差）：模型预测值在不同数据集上的变化程度，衡量了模型的稳定性。方差较大的模型可能对训练数据过度拟合。
  9. Overfitting（过拟合）：模型在训练数据上表现良好，但在新数据上表现较差。这通常是因为模型过于复杂，捕捉到了训练数据中的噪声。
  10. Underfitting（欠拟合）：模型在训练数据和新数据上都表现不佳。这通常是因为模型过于简单，无法捕捉到数据中的基本关系。

  这些术语在论文中被用来描述和解释Stacking方法的原理、优点和局限性。通过理解这些术语，可以更好地理解Stacking方法的工作原理和应用场景。

称呼说明

• 这里元估计器(元学习器)指的是合并初级估计器的次级估计器,而不是初级估计器

相关原理

• 堆叠法 (Stacking)是一种创建集成的方法，它使用一个元估计器(次级估计器)去合并基估计器(初级估计器)的预测结果。
• 堆叠法有时也被称为混合法，会增加第二个监督学习问题：元估计器必须被训练去使用基础估计器的预测结果来预测响应变量的值。
• 为了训练一个堆叠集合，首先需要使用训练集去训练基础估计器。
• 和套袋法以及推进法不同，堆叠法可以使用不同种类的基础估计器。
  • 例如，一个随机森林可以和一个逻辑回归分类合并。
  • 接下来，基础估计器的预测结果和真实情况会作为元估计器的训练集。
• 元估计器可以在相比投票和平均更复杂的情况下学习合并基础估计器的预测结果。

自定义简单的StackingClassifier

• scikit-learn 现在已经提供了Stacking系列方法

• 我们也可以扩展 base.BaseEstimator 类去创建自己的StackingClassifer。

• 在下面的例子中，使用一个单一决策树作为元估计器，基础估计器包括一个逻辑回归分类器和一个 KNN 分类器。

• 我们使用类的预测概率作为特征，而不是使用类的预测标签。

• 另外，我们使用 make_classification函数创建一个人工分类数据集。接着，训练并评估每一个基础估计器。最后，训练并评估集合，它具有更好的准确率。

• import numpy as np 
  from sklearn.model_selection import train_test_split 
  from sklearn.neighbors import KNeighborsClassifier 
  from sklearn.tree import DecisionTreeClassifier 
  from sklearn.linear_model import LogisticRegression 
  from sklearn.datasets import make_classification 
  from sklearn.base import clone, BaseEstimator, TransformerMixin,ClassifierMixin class StackingCustomClassifier(BaseEstimator, ClassifierMixin, TransformerMixin): def __init__(self, classifiers): self.classifiers = classifiers self.meta_classifier = DecisionTreeClassifier() def fit(self, X, y): for clf in self.classifiers: clf.fit(X, y) self.meta_classifier.fit(self._get_meta_features(X), y) return self def _get_meta_features(self, X): probas = np.asarray([clf.predict_proba(X) for clf in self.classifiers]) return np.concatenate(probas, axis=1) def predict(self, X): return self.meta_classifier.predict(self._get_meta_features(X)) def predict_proba(self, X): return self.meta_classifier.predict_proba(self._get_meta_features(X)) X, y = make_classification( n_samples=1000, n_features=50, n_informative=30, n_clusters_per_class=3, random_state=11) 
  X_train, X_test, y_train, y_test = train_test_split(X, y, 
  random_state=11) lr = LogisticRegression() 
  lr.fit(X_train, y_train) 
  print('Logistic regression accuracy: %s' % lr.score(X_test, 
  y_test)) knn_clf = KNeighborsClassifier() 
  knn_clf.fit(X_train, y_train) 
  print('KNN accuracy: %s' % knn_clf.score(X_test, y_test)) # Out[1]: 
  # Logistic regression accuracy: 0.816 
  # KNN accuracy: 0.836 # In[2]: 
  base_classifiers = [lr, knn_clf] 
  stacking_clf = StackingCustomClassifier(base_classifiers) 
  stacking_clf.fit(X_train, y_train) 
  print('Stacking classifier accuracy: %s' % stacking_clf.score(X_test, 
  y_test)) 
  

主要步骤

Stacking 算法的主要步骤如下：

1. 准备数据：将数据集划分为训练集和测试集。
2. 训练基学习器：选择多个基学习器（例如，决策树、支持向量机、神经网络等），并在训练集上训练它们。
3. 生成元特征：使用训练好的基学习器对训练集进行预测。将这些预测结果作为新的特征（称为元特征），并创建一个新的训练集。通常，我们使用 K 折交叉验证的方法生成元特征，以避免过拟合。
4. 训练元学习器：使用生成的元特征和训练集的目标变量训练元学习器。元学习器可以是任何模型，例如线性回归、逻辑回归或梯度提升树等。
5. 预测：首先，使用基学习器对测试集进行预测，然后将这些预测结果作为元特征输入到元学习器中，最后由元学习器生成最终预测结果。

Stacking 的优点

• 通过结合多个基学习器的预测能力，Stacking 可以提高模型的泛化性能。
• Stacking方法的优势在于它可以有效地整合多个模型的预测能力，使得集成后的模型具有更强的泛化能力。此外，Stacking可以很好地处理基础模型之间的异质性，使得不同类型的模型可以共同为提高预测性能做出贡献。
• Stacking 可以利用不同类型的基学习器，从而充分利用它们的多样性。

Stacking 的缺点

• Stacking 涉及多个模型的训练和预测，因此计算成本较高。
• Stacking 模型的可解释性较差，因为它是一个多层次的集成模型。
• 局限性：Stacking方法的主要局限性在于其计算复杂度较高，因为需要训练多个基础模型和一个元学习器。此外，如果基础模型的预测结果相关性较高，那么Stacking方法的性能可能受到限制，因为元学习器难以从高度相关的基础模型预测中获取额外的信息。为了解决这个问题，可以尝试使用多样性较高的基础模型以提高Stacking的性能。

在实践中，为了获得更好的性能，可以尝试使用不同类型和参数设置的基学习器，以及调整元学习器的类型和参数。此外，可以通过特征工程、调整训练过程中的抽样策略等方法进一步优化模型。

• 更多内容参考学习策略:学习法|stacking

小结

• Stacking（堆叠）是一种集成学习方法，它结合了多个基本模型（也称为基学习器）的预测结果，以生成一个新的、更强大的模型（也称为元学习器或次级模型）。Stacking其主要目的是通过结合多个基础模型的预测结果来提高总体预测性能。与Bagging和Boosting等其他集成方法不同，Stacking使用一个元学习器（也称为次级模型或模型堆叠器）将基础模型的预测结果作为输入，训练出一个最终预测模型。Stacking的核心思想是借助多个模型的不同优势，捕捉到数据中的更多信息和特征，从而实现更高的预测正确率。
• 以下是Stacking方法的详细介绍和总结：
  1. 基础模型：在Stacking方法中，首先需要训练一组基础模型（也称为第一层模型）。这些模型可以是相同的算法，也可以是不同的算法。例如，可以使用决策树、支持向量机、神经网络等多种机器学习算法作为基础模型。
  2. 训练集和验证集：为了训练元学习器，需要将原始训练数据集划分为训练集和验证集。训练集用于训练基础模型，而验证集用于构建元学习器的输入特征。
  3. 基础模型预测：使用训练集训练基础模型后，将验证集输入到这些模型中得到预测结果。这些预测结果将作为元学习器的输入特征。需要注意的是，为了避免过拟合，可以使用K折交叉验证的方法在不同的数据子集上训练基础模型，并将不同子集上的预测结果拼接起来，作为元学习器的输入。
  4. 元学习器训练：将基础模型在验证集上的预测结果作为输入特征，将验证集的真实标签作为输出标签，训练元学习器。元学习器可以是任何适用的机器学习算法，如线性回归、逻辑回归或梯度提升树等。
  5. 预测：在测试集上进行预测时，首先使用基础模型对测试集进行预测，然后将这些预测结果作为特征输入到元学习器中，得到最终的预测结果。