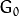Lucas定理(大组合数取模)
一、定义:
当n、m为大数,p为素数时, Lucas定理是用来求 c(n,m) mod p的 值。 适用领域范围 : 在数论中求大组合数取模。
表达式: C(n,m)%p=C(n/p,m/p)*C(n%p,m%p)%p
二、定理内容:
Lucas定理:我们令 n=sp+q , m=tp+r . (q ,r ≤p)
那么: 
(在编程时你只要继续对  调用Lucas定理即可。
调用Lucas定理即可。
代码可以递归的去完成这个过程,其中递归终点为 t = 0 ;
时间 O(logp(n)*p))。
三、证明及推导: (该过程边看边写效果更佳!)
要证:C(n,m)%p=C(n/p,m/p)*C(n%p,m%p)%p
即证:C(n,m)=C(n/p,m/p)*C(n%p,m%p)
证明:
已知p是素数,n、m、p为整数。
1.由二项式定理得:
 ,且
,且 
2.由费马小定理得:
(1)式 :(1+x)^p ≡ (1+x)(mod p).
(2)式 :(1+x^p)≡ (1+x)(mod p). (因为x^p与x取模p同余,同时加1也同余 )
则由上式可知:
(1+x)^p ≡ (1+x^p)(mod p) (记为(3)式)
3.n = n/p*p + n%p . 则:
(1+x)^p(mod p) = (1+x)^(n/p*p)*(1+x)^(n%p)(mod p)
由式3得: (1+x)^p(mod p)= (1+x^p)^(n/p)*(1+x)^(n%p)(mod p)
将上式由二项式公式可转化为:(这一排你用手写看一下吧,这编辑器里太难敲了……)
∑(n,z=0)C(n,z)* x^z (mod p)=∑(n/p,i=0)C(n/p,i)* x^(p*i)*∑(n%p,j=0)C(n%p,j)* x^j( mod p)
任意一个Z,必存在一个i,j满足:x^z = x^(p*i)*x^j(即满足:n = n/p*p + n%p),当且仅当: i=z/p,j=z%p 时成立
此时:
C(n,m)=C(n/p,m/p)*C(n%p,m%p) 成立
得证!
代码求解过程中,不断将C(n/p,m/p)拆分化简,实质是一直在计算C(n%p,m%p),即:
C(n,m)%p=C(n/p,m/p)*C(n%p,m%p)%p
等价于C(n,m)%p=C(n/p/p,m/p/p)*C(n/p%p,m/p%p)%p
等价于C(n,m)%p=C(n/p/p/p,m/p/p/p)*C(n/p/p%p,m/p/p%p)%p
等价于…
直到拆分至m=0,递归完成。
四、逻辑代码:
#include<iostream>
using namespace std;
typedef long long ll;ll fastmod(ll a,ll b,ll p) //费马小定理
{ll cnt=1;while(b){if(b&1)cnt=(cnt*a)%p;a=(a*a)%p;b>>=1;}return cnt;
}ll Comb(ll a,ll b,ll p) //组合数
{ll ca=1,cb=1,tmp=1;;if(a<b) return 0;if(a==b) return 1;if(b>a-b) b=a-b;for(ll i=0;i<b;i++){ca=(ca*(a-i))%p;cb=(cb*(b-i))%p;}tmp=(ca*fastmod(cb,p-2,p))%p; //除法转换求逆元return tmp;
}ll Lucas(ll n,ll m,ll p)
{ll ans=1;while(n&&m&&ans){ans=(ans*Comb(n%p,m%p,p))%p; //拆分+递归n/=p;m/=p;}return ans;
}int main()
{ll n,m,p;while(cin>>n>>m>>p){ll ans=Lucas(n,m,p);cout<<ans<<endl;}return 0;
}
~step by step