x o u t = x i n − k s + 1 x_{out} = \frac{x_{in} - k}{s} + 1 xout=sxin−k+1
如果不考虑padding,卷积输出的feature map的计算公式如上,那么 x i n = ( x o u t − 1 ) ∗ s + k x_{in} = (x_{out} - 1) * s + k xin=(xout−1)∗s+k。因此计算模型的感受野可以从最后一层往前推。下面举个例子说明:
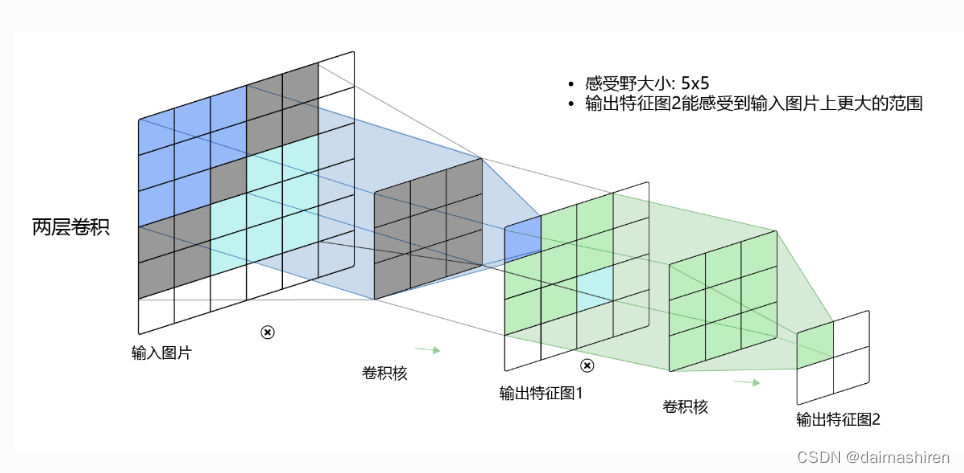
图片来自于https://paddlepedia.readthedocs.io/en/latest/tutorials/CNN/convolution_operator/Convolution.html
一个输入大小为6x6的图像经过两层大小为3x3的卷积核之后,输出特征图变为2x2。现在要计算输出的这个特征图上的每个点对应输入的6x6的图像上多大范围的像素点(感受野)。很直观的,输出的2x2图像上每个点来自于中间特征图的3x3区域。即:
x i n = ( x o u t − 1 ) ∗ s − k = ( 2 − 1 ) × 1 + 3 = 3 x_{in} = (x_{out} - 1)*s - k = (2 - 1)\times 1 + 3 = 3 xin=(xout−1)∗s−k=(2−1)×1+3=3
那么中间的特征图上点影响多大范围的来自第一个特征图像素点?类似的过程代入以上公式:
x i n = ( x o u t − 1 ) ∗ s + k = ( 3 − 1 ) ∗ 1 + 3 = 5 x_{in} = (x_{out} - 1) * s + k = (3 - 1) * 1 + 3 = 5 xin=(xout−1)∗s+k=(3−1)∗1+3=5
因此我们得到输出的2x2的特征图上的点对应于原始特征图上5x5范围的像素点,即感受野为5x5。池化层的感受的计算同上。如果是遇到空洞卷积的感受野计算,可以先把空洞卷积转换成等效的卷积核 (参考: 直观理解Dilated Convolution)
空洞卷积的等效卷积核大小为 k ′ = k + ( k − 1 ) ( d − 1 ) = d ( k − 1 ) + 1 k' = k + (k-1)(d-1) = d(k-1)+1 k′=k+(k−1)(d−1)=d(k−1)+1,其中d为膨胀率。换成等效卷积核后再套用以上方法计算感受野即可。
通俗理解CNN感受野的计算方法
news/2024/11/24 8:31:02/
相关文章
APP外包项目的线上维护方案
APP的使用已经非常普及,不论是2C还是2B的APP都已经渗透到了我们生活的方方面面,对于APP的开发公司来说APP项目的线上维护是一个非常重要的问题。如果APP项目比较重要而且用户规模比较大,那更需要专业的技术团队来维护。今天和大家分享这方面的…
[LeetCode周赛复盘] 第 344 场周赛20230507
[LeetCode周赛复盘] 第 344 场周赛20230507 一、本周周赛总结6416. 找出不同元素数目差数组1. 题目描述2. 思路分析3. 代码实现 6417. 频率跟踪器1. 题目描述2. 思路分析3. 代码实现 6418. 有相同颜色的相邻元素数目1. 题目描述2. 思路分析3. 代码实现 6419. 使二叉树所有路径…
Qt5.9学习笔记-事件(四)Qt5.9中常见事件
⭐️我叫忆_恒心,一名喜欢书写博客的在读研究生👨🎓。 如果觉得本文能帮到您,麻烦点个赞👍呗! 近期会不断在专栏里进行更新讲解博客~~~ 有什么问题的小伙伴 欢迎留言提问欧,喜欢的小伙伴给个三…
聚焦丨酷雷曼荣列XRMA联盟成员单位
自“元宇宙”概念兴起之初,酷雷曼VR所属北京同创蓝天云科技有限公司就积极布局、探索和实践。2022年12月,酷雷曼VR成功加入虚拟现实与元宇宙产业联盟(XRMA),正式被接纳为联盟成员单位,意味着酷雷曼公司将进…
第一行代码 第八章 运用手机多媒体
第八章 运用手机多媒体
使用通知
通知(Notification)是Android系统中比较有特色的一个功能,当某个应用程序希望向用户发出一些提示信息,而该应用程序又不在前台运行时,就可以借助通知来实现。发出一条通知后…
全面理清概念,C风格字符串(多重定义方式,区别,易错点)
C风格字符串 C风格字符串是一种在C语言中表示字符串的方式,它是通过字符数组来实现的。 C风格字符串是一系列字符,以空字符(‘\0’)作为结束标志。这意味着在声明并定义一个C风格字符串时,我们需要为数组分配比实际字符…

![[LeetCode周赛复盘] 第 344 场周赛20230507](https://img-blog.csdnimg.cn/86d2dd453c954ea48709136be958b4b4.png)