1. 基本概念

用大津法最终会得到一个阈值，使用该阈值将图像进行二值化。大于这个阈值的，像素值变成1；小于阈值的，像素值变成0。 原本图像的像素范围是从0~255，大津法的思想很简单，就是遍历这256个阈值，对每个阈值，都进行一次二值化。最终看哪个阈值下二值化的结果最合适。接下来就介绍遍历的公式。

2. 公式

这里我将像素值为1的称作前景，像素值为0的称作后景。
大津法的最终公式为很多小的计算拼起来的，如下

2.1 后景像素比w0

$${\omega }_0=\frac{后景像素数量}{图像宽\ast 图像高}\text{\hspace{1em}(1)}$$

2.2 前景像素比w1

$${\omega }_1=\frac{前景像素数量}{图像宽\ast 图像高}\text{\hspace{1em}(2)}$$

2.3 后景平均灰度u0

$${\mu }_0=\frac{{\sum }_{all}后景像素的值}{后景像素数量}\text{\hspace{1em}(3)}$$

2.4 前景平均灰度u1

$${\mu }_1=\frac{{\sum }_{all}前景像素的值}{前景像素数量}\text{\hspace{1em}(4)}$$

2.5 公式汇合

根据式1~4，可以得到(5)
$$\mu ={\omega }_0\ast {\mu }_0+{\omega }_1\ast {\mu }_1、\text{\hspace{1em}(5)}$$
其中$\mu$是图像的平均灰度

而大津法的公式为
$$g={\omega }_0\ast ({\mu }_0-\mu {)}^2+{\omega }_1\ast ({\mu }_1-\mu {)}^2\text{\hspace{1em}(6)}$$
将(5)带(6)，可以得到(7)
$$g={\omega }_0{\omega }_1({\mu }_0-{\mu }_1{)}^2\text{\hspace{1em}(7)}$$

3. 代码

代码部分中，上述的公式都会体现出来。已经被注释所标注。

import numpy as np
import math'''
Summary:大津阈值分割
Paramaters：img - 输入的灰度图像 是二维矩阵
'''
def OTSU(img):# 类间方差g初始最小g_raw = -1# 要返回的阈值T_return = 0# 获得图像大小M_N = img.shape[0]*img.shape[1]# 大津阈值算法for T in range(256):# 获取阈值大于T和小于T的两个列表array0 = img[img<T] array1 = img[img>T]# 算出w0和w1w0 = len(array0)/M_N  # 公式1w1 = len(array1)/M_N  # 公式2# 算出μ0和μ1 这里需要特判除数为0if len(array0) == 0:mu0 = 0else:mu0 = sum(array0)/len(array0) # 公式3if len(array1) == 0:mu1 = 0else:mu1 = sum(array1)/len(array1)  # 公式4# 算出gg=w0*w1*math.pow((mu0-mu1),2)  # 公式6if g > g_raw:g_raw = gT_return = Treturn T_return

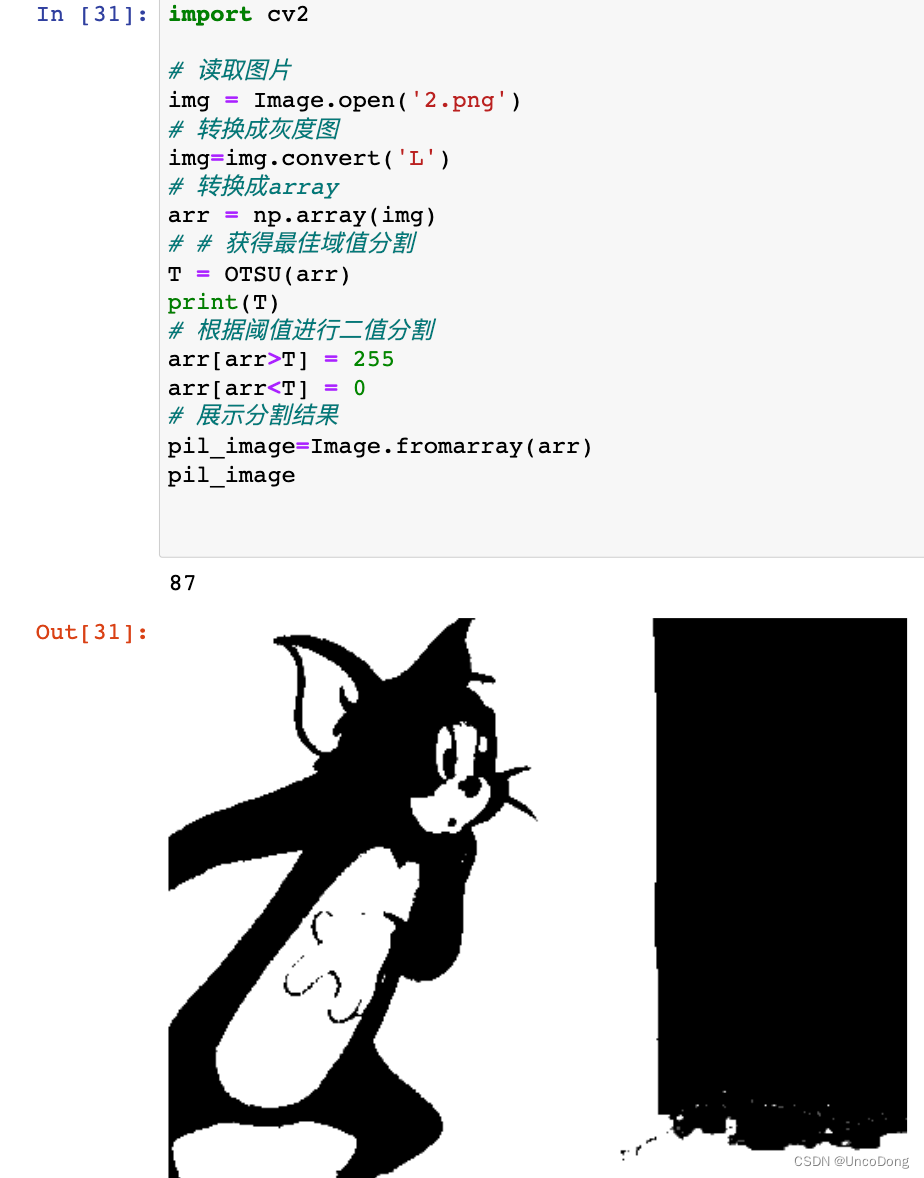
使用该图进行测试，效果如下所示

import cv2# 读取图片
img = Image.open('2.png')
# 转换成灰度图
img=img.convert('L')
# 转换成array
arr = np.array(img)
# # 获得最佳域值分割
T = OTSU(arr)
print(T)
# 根据阈值进行二值分割
arr[arr>T] = 255
arr[arr<T] = 0
# 展示分割结果
pil_image=Image.fromarray(arr)
pil_image