• 本题帮助我们进一步理解回溯的含义，在回溯算法中，当一条路径（一种解法）被完全探索后，我们需要撤销（回溯）当前步骤的选择，然后尝试其他可能的路径（其他解法）。这也是为什么本题同一分支的递归内，同一行只可能存在一个皇后的原因。

51.N皇后

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

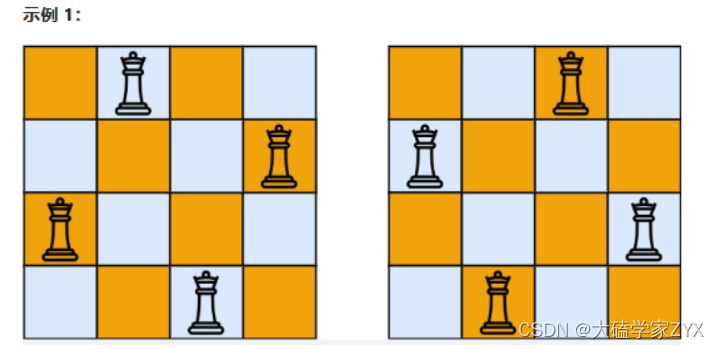
输入：n = 4
输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

输入：n = 1
输出：[["Q"]]

提示：

• 1 <= n <= 9

思路

我们之前用回溯解决的问题，主要是组合、切割、子集、排列问题。而N皇后这一类问题是处理二维矩阵，这属于棋盘问题。

这个题主要是在n*n的棋盘里面放n个皇后，同一行/同一列/同一斜线里，都不能出现两个皇后。

如果暴力枚举所有皇后的位置，应该嵌套4个for循环，第一个for遍历第一行，里面嵌套3个for分别遍历第二行，第三行和第四行。每一行枚举对应行的位置分别放皇后，然后检查这个位置能不能放。

但是这个棋盘不一定是4*4，因此for循环的遍历就行不通。因此必须用回溯，n*n的棋盘就递归n层。

树形图

这种二维矩阵问题，画清楚树形图也非常重要。以3*3的棋盘为例，放置3个n皇后的树形图如下：

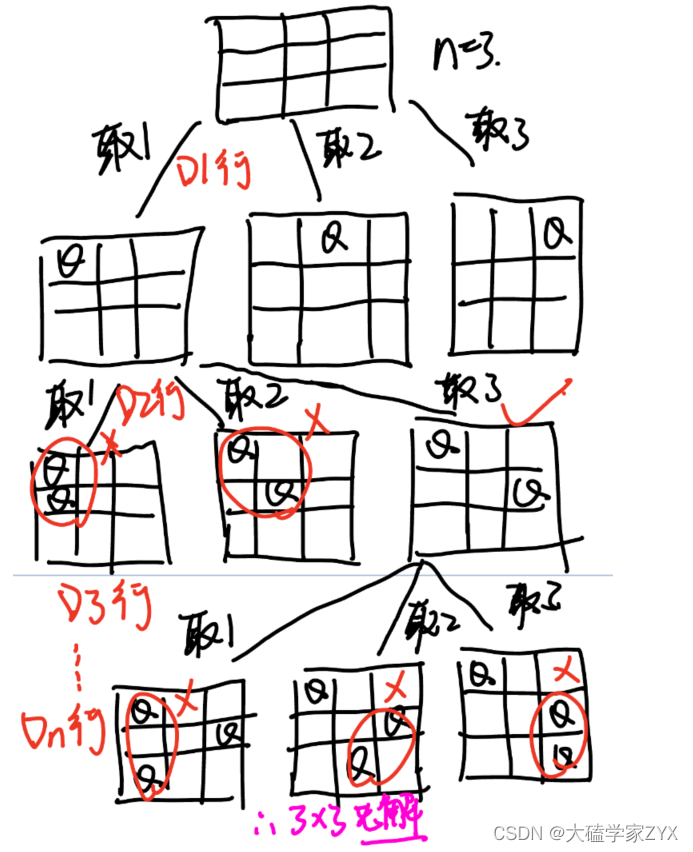
通过树形结构进一步明确棋盘问题的搜索过程，每一层里面都是取1/取2/取3，但是每一层递归里面对应的是不同的行！取1/2/3是每一行对应的列。

树的深度就是n行数，宽度也是n，是列数。画出来树形结构之后，逻辑就清晰很多。

重要逻辑：棋盘的表示法

本题最开始卡住，一个问题就是我搞不明白怎么访问棋盘的元素。

本题的棋盘，是通过[“.Q…”,“…Q”,“Q…”,“…Q.”]这个vector<string>数组，来表示下标[i][j]的二维棋盘的。一个单独的vector一维数组，就可以表示二维的棋盘。

为什么一个一维的vector<string>数组，就能表示一个下标[i][j]访问的二维棋盘？而不是用一个二维的数组来表示？

这是因为在C++中，string本身就被设计为字符数组，所以我们可以通过索引[i]直接访问一个string里面的元素，比如".Q.."这个string，就可以用string[1]来访问皇后'Q'。

vector<string>类型的对象可以视为二维数组（或者说是一个棋盘），每个string对象是一行，而每个string内部的字符则构成这行的列。因此，你可以通过两层索引来定位特定的行和列，即特定的字符。

一维字符数组vector表示棋盘的情况如图：

result里面”三维数组“的获取

string是字符数组，因此可以通过索引来访问其内部的字符。这就导致**vector<vector<string>>作为一个二维字符串数组，有了类似三维数组的表现**。尽管严格来说，它还是二维数组，只不过它的元素（string对象）可以进一步通过索引访问。

也就是说，对于vector<vector<string>>类型的对象，可以先用两层索引访问到字符串，再加一层索引访问字符串内部的字符。

例如二维字符数组vector<vector<string>>vec[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]，就代表着两个4*4的棋盘！如果我们想访问第一个棋盘里第一行的皇后字符'Q'，我们可以直接使用vec[0][0][1]。

注意，在计算下标的时候，我们不需要管vec[0][0]这个字符串本身带有的双引号。

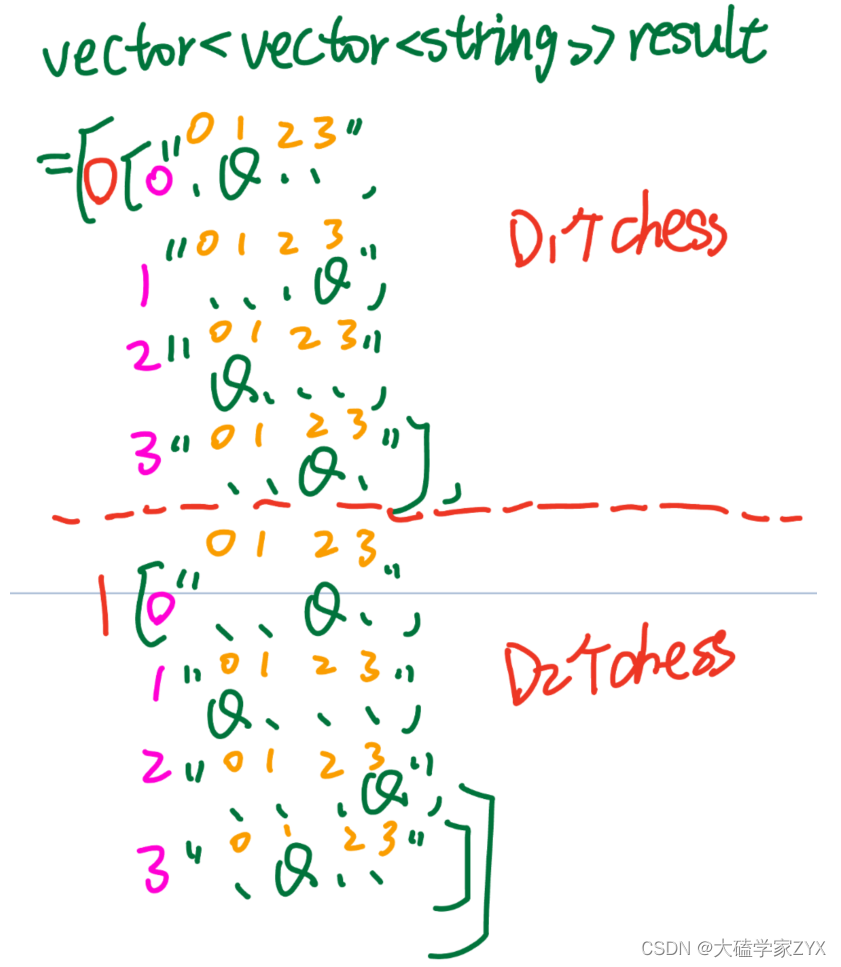
result中”三维数组“分别的下标情况如图所示：

（注意第一个chessBoard本身就是一维数组表示的，并不需要在意下标是横着还是竖着的情况）

补充1：双引号问题

关于双引号的问题，字符串常量在C++代码中确实是用双引号括起来的，但是这只是代码的一部分，它们不会存储在string对象中。因此，你访问string内部字符时，索引是从0开始的，不会包括那些双引号。所以vec[0][0][1]的确会返回'Q'，而不需要考虑双引号。

补充2：二维string数组下标访问的问题

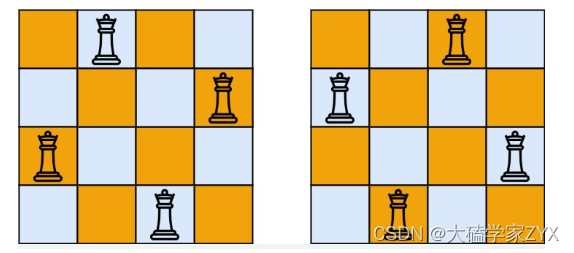
在C++中，数组和vector的索引都是从0开始的。所以，对于给出的vector<vector<string>>vec[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]，使用vec[1][1][0]来访问的时候，第一个下标1对应的是第二个棋盘，第二个下标1对应的是第二行，第三个下标0则对应该行的第一个字符。

因此，vec[1][1][0]会访问到第二个棋盘（即第二个vector<string>）中第二行的第一个字符，也就是字符'Q'。如下图：

回溯部分

• 每一个棋盘是一个二维数组，result就是一个三维数组
• 用递归控制每一行row，再用for循环遍历每一行里面的情况

//参数传入行，每次递归都是行数+1
void backtracking(vector<vector<string>>&result,vector<string>&chessBoard,int n,int row){//本题也是叶子节点收获结果，row是n的时候就是叶子节点if(row==n){//如果走到叶子节点了，一定是合法棋盘result.push_back(chessboard);return;}//每一列都要遍历，从0开始for(int i=0;i<n;i++){//i=0，判断这一行，i=0的位置放皇后是不是合法棋盘，合法性函数单独写！//位置就是(row,i)if(isValid(chessBoard,row,i)==true){//如果合法，就在棋盘上这个位置放皇后。chessBoard[row][i]=='Q';//放了皇后之后直接下层递归，注意下一层递归遍历第二行！backtracking(result,chessBoard,n,row+1);//回溯chessBoard[row][i]=='.';}}
}

合法性判断函数部分

本题回溯部分，搞清楚了逻辑并不难，比较难想的是合法性判断函数这里。

合法性函数要单独写，原理就是判断传入棋盘和当前位置(row,i)的时候:

• 行里面有没有重复出现皇后
• 列里面有没有重复出现皇后
• 45°角和135°角有没有重复出现皇后。

//判断一个chess棋盘中，[row,i]的位置是否合法
bool isValid(vector<string>&chessBoard,int row,int i,int n){//检查同行，实际上并不需要检查//for(int num=0;num<=i;num++){//    if(chessBoard[row][num]=='Q'){//        return false;//    }//}//检查同列for(int num1=0;num1<=row;num++){if(chessBoard[num1][i]=='Q'){return false;}}//检查45°角for(int m=row-1,num=i-1;m>=0&&num>=0;m--,num--){if(chessBoard[m][num]=='Q'){return false;}}//检查135°角for(int m=row-1,int num=i+1;m>=0&&num<n;m--,num++){if(chessBoard[m][num]=='Q'){return false;}}
}

检查[row,i]位置45°和135°斜线有无皇后的方式

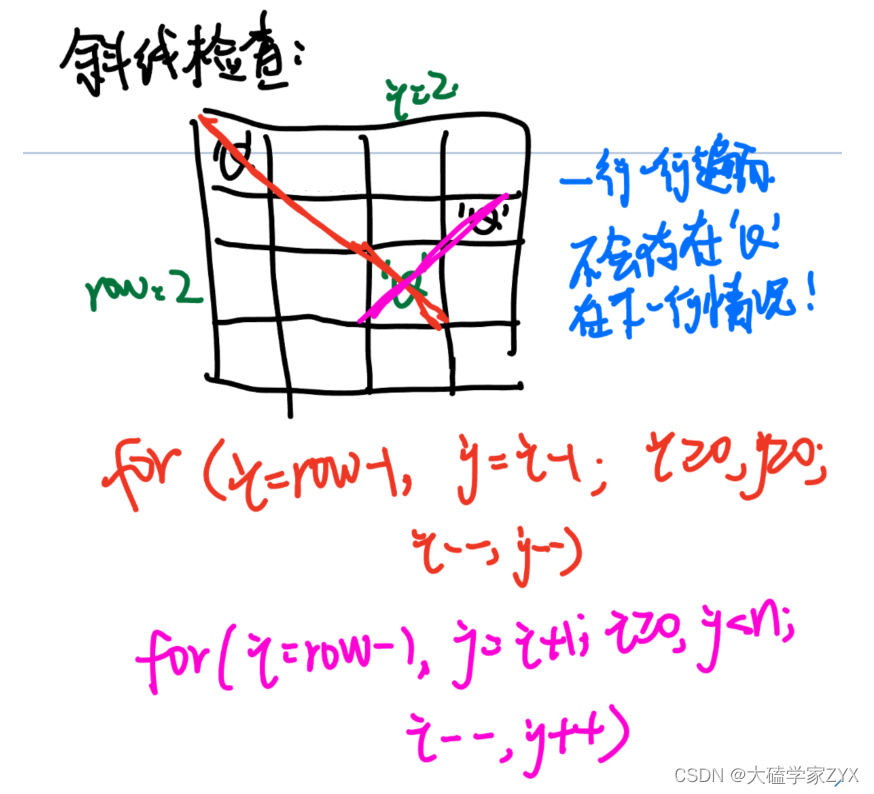
斜线检查，一个很重要的点就是，我们回溯遍历的时候是按照row来一行一行向下遍历。

因此，斜线的情况只可能存在于row上面的行里，不可能出现在row下面的行里！因为下面的行还没遍历到，不可能往里面放皇后！

斜线检查示意图如图。

//45
for(int num=row-1, int num2=i-1;num>=0&&num2>=0;num--,num2--){if(chessBoard[num][num2]=='Q'){return false;}
}
//135
for(int num = row-1,int num2 = i+1;num>=0&&num2<n;num--,num2++){if(chessBoard[num][num2]=='Q'){return false;}
}

完整版

class Solution {
public:bool isValid(vector<string>&chessBoard,int row,int i,int n){//为什么不需要检查同行？//for(int num=i;num>=0;num--){//    if(chessBoard[row][num]=='Q'){//        return false;//    }//}//同列有无元素for(int num=row;num>=0;num--){if(chessBoard[num][i]=='Q'){return false;}}//45°有无元素for(int num1=row,num2=i;num1>=0&&num2>=0;num1--,num2--){//两个条件需要&&并列！if(chessBoard[num1][num2]=='Q'){return false;}}//135°有无元素for(int num1=row,num2=i;num1>=0&&num2<n;num1--,num2++){if(chessBoard[num1][num2]=='Q'){return false;}}return true;}void backtracking(vector<vector<string>>&result,vector<string>&chessBoard,int n,int row){//终止条件if(row==n){result.push_back(chessBoard);return;}//单层递归for(int i=0;i<n;i++){//如果位置合法，就加入皇后if(isValid(chessBoard,row,i,n)==true){chessBoard[row][i]='Q';//递归,下一行遍历row+1backtracking(result,chessBoard,n,row+1);//回溯，找下一种解法chessBoard[row][i]='.'; }}}vector<vector<string>> solveNQueens(int n) {//输入只有棋盘大小n，需要先创建n*n的空棋盘存在vector<string>里面vector<string>chessBoard(n,string(n,'.'));//创建结果数组vector<vector<string>>result;//靠遍历row来进行递归int row=0;backtracking(result,chessBoard,n,row);return result; }
};

重要逻辑：为什么不需要判断同一行是不是有皇后

因为在我们这种写法的单层搜索的过程中，每一层递归，只会选for循环（也就是同一行）里的一个元素，所以不用去重了。

我们可能会想，for循环终止条件难道不是i<n吗？i<n不就意味着每个位置都会被搜索吗？

for循环的终止条件确实是 i<n。然而，当在for循环内部调用递归函数 backtracking 时，如果在该行找到了一个可放置皇后的位置，代码会立即进入下一层递归，开始在下一行放置皇后。

但是，这并不意味着原本的for循环就停止了。当递归调用返回后（也就是说，所有可能的皇后位置在下一行都已经被尝试过了），程序会继续进行for循环，尝试在当前行的下一个位置放置皇后。

此时，第一种方案时这行row放置皇后的情况，已经被pop出去了。也就是回溯撤销了！

这就是“回溯”这个词的含义。我们首先尝试一个可能的解决方案（在当前行的某个位置放置皇后），然后递归地尝试解决剩余的问题（在下一行放置皇后）。如果这导致了一个有效的解决方案，那么我们就找到了一个解决方案。否则，我们会**“回溯”，撤销我们最近的选择**（通过 chessBoard[row][i] = '.'; 这一行代码），然后尝试下一个可能的选择。

在这种情况下，我们的目标是找到所有可能的解决方案，而不仅仅是找到一个解决方案。所以即使我们在当前行找到了一个可以放置皇后的位置，我们也需要尝试其他位置，看看是否有其他可能的解决方案。这就是为什么我们在递归调用后需要继续进行for循环的原因。

在回溯算法中，当一条路径（一种解法）被完全探索后，我们需要撤销（回溯）当前步骤的选择，然后尝试其他可能的路径（其他解法）。

debug测试

for循环多个条件的情况书写错误

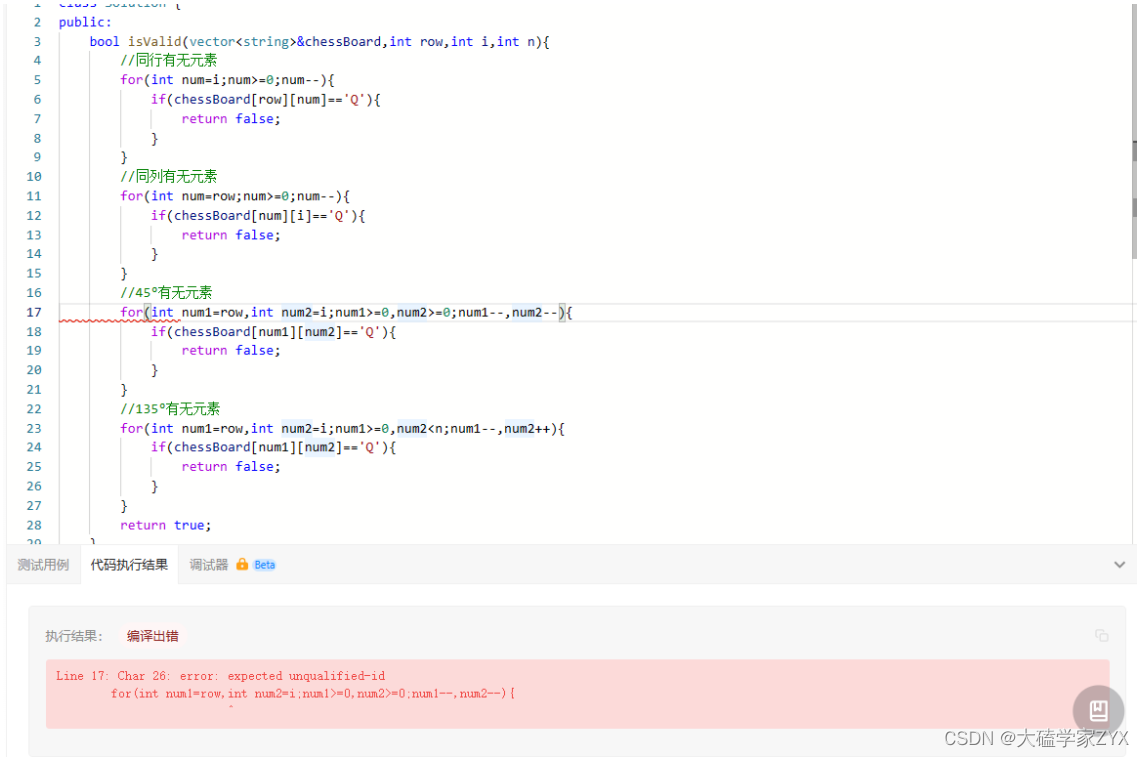
for循环的写法错误，逗号分隔的话不需要再定义！

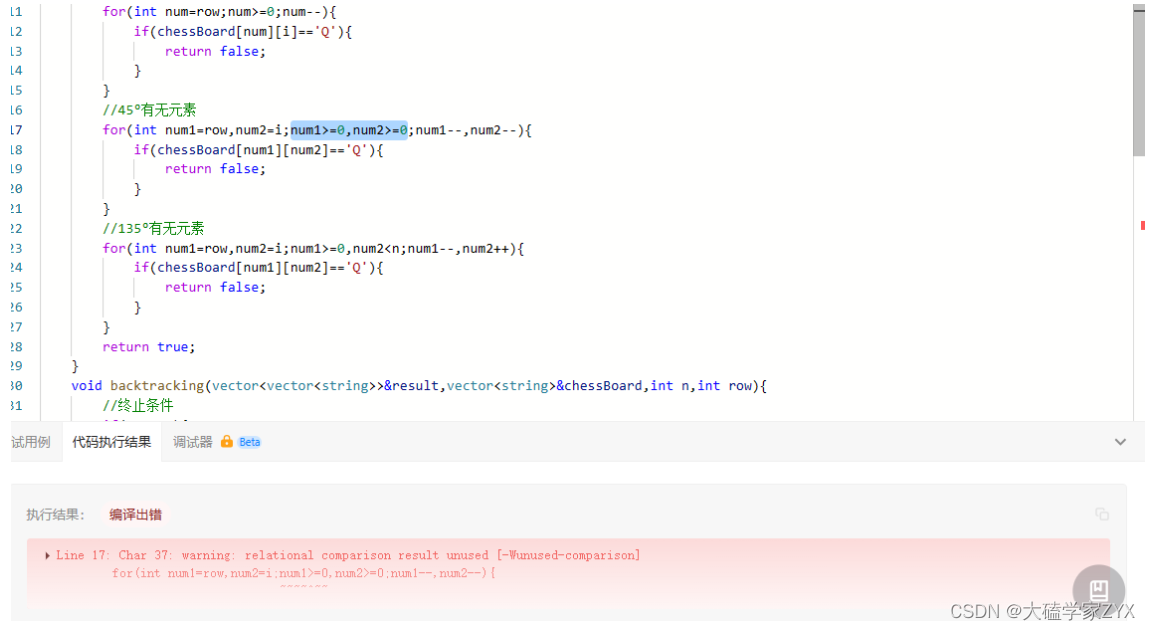
两个条件需要&&并列！

逻辑错误：出现了大量其余结果

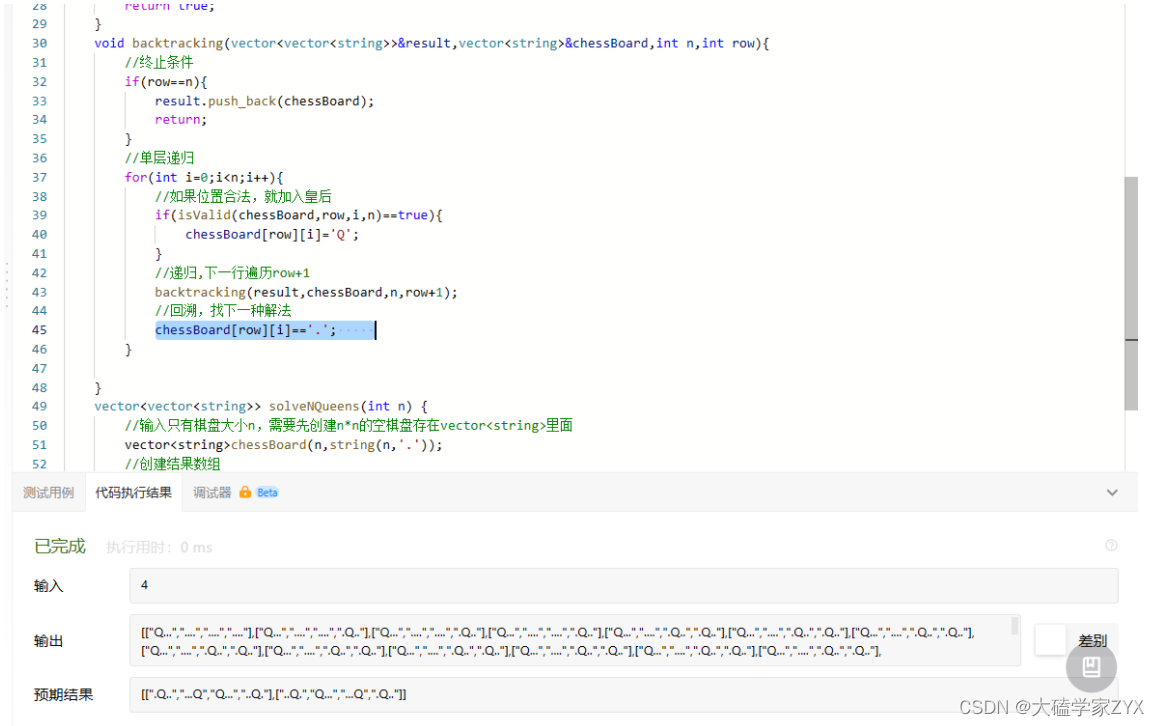
这个错误，实际上是因为原始代码中，这个部分必须放在If的里面！也就是说，只有合法的情况，才能向下递归！因此，向下递归的操作必须放在if(合法性判断)的里面！

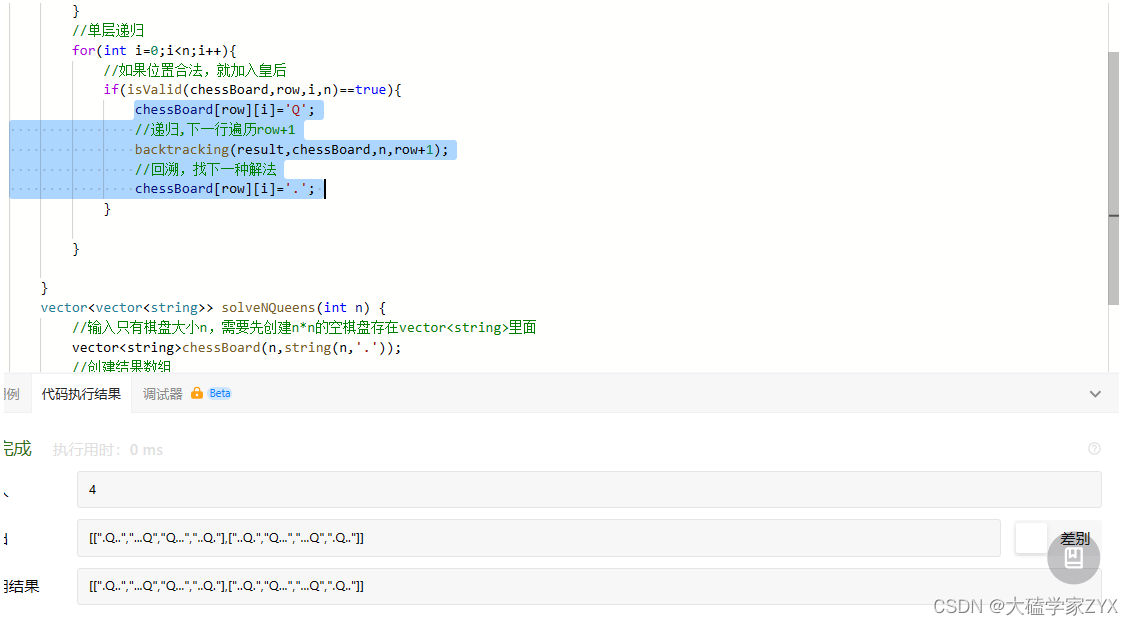
修改成这样后正常。

补充知识

字符串数组vector<string>的创建

由于vector<string>本身已经算是一个二维数组（实际上还是一维的），创建的时候需要把vector数组大小和内部字符串的大小都说清楚。

for循环中第二部分两个条件的连接问题

for循环的第二部分条件部分，如果存在两个以上的条件，绝对不能用逗号来连接两个条件。

例如以下代码：

for(int num1=row,num2=i;num1>=0&&num2>=0;num1--,num2--)

如果我们写成

for(int num1=row,num2=i;num1>=0,num2>=0;num1--,num2--)//错误，第一个条件无效

那么这个循环只会在 num2 >= 0 时执行，而 num1 >= 0 并不会影响循环的执行。在 for 循环的条件部分使用逗号并不会使得循环在所有条件都满足时执行，而是只会检查最后一个条件！

这是因为c++中，逗号操作符如果用来在一行内执行多个表达式，那么这些表达式会从左到右依次执行，但整个表达式的值是最右边的表达式的值！

cpp中逗号操作符功能

在 C++ 中，逗号操作符有两个功能。

1. 在声明多个变量时，逗号可以用来分隔变量。例如，int num1 = 0, num2 = 0;。

2. 逗号操作符也可以用来在一行内执行多个表达式。这些表达式会从左到右依次执行，但整个表达式的值是最右边的表达式的值。

   例如，int num1 = (num2 = 3, num2 + 2); 在这个表达式中，首先执行 num2 = 3，然后计算 num2 + 2，并把结果赋给 num1。因此，num1 的值会是 5。

因此，在 for 循环的条件部分使用逗号并不会使得循环在所有条件都满足时执行，而是只会检查最后一个条件。

所以，如果想要 for 循环在多个条件都满足时执行，必须使用 && 操作符，而不是逗号。

时间复杂度

本题时间复杂度是O(n!)。

当我们在第一行放置皇后时，有 N 种可能的位置。对于每一种第一行的放置方式，我们在第二行也有 N-1 种可能的位置（因为不能和第一行的皇后在同一列或对角线），以此类推。所以，这实际上是一种全排列的情况，总共有 N*(N-1)*(N-2)*...*1，也就是 N! 种可能的皇后放置方式。

不过实际上，由于我们在放置皇后时还考虑了不能在对角线上，所以实际的搜索空间会比 N! 小一些。但是，当 N 很大时，我们通常忽略这种差别，所以时间复杂度仍然可以看作是 O(N!)。

另外，虽然每次递归时，都是从 i=0 开始搜索，但实际上，并不是每个 [row, i] 的位置都会对应搜索整个棋盘。因为当 [row, i] 位置放置了皇后之后，我们就会进入下一行，而不会再考虑当前行的其他位置。所以，实际上，在任何一次递归搜索中，我们都只是搜索了棋盘的一个部分，而不是整个棋盘。

总结

vector<string>而不是二维int数组来表示棋盘的原因

• 一个二维棋盘，可以由vector<vector<int>>或者vector<string>来表示。
• 但是对于N皇后这个问题，我们需要频繁地在棋盘的某个位置上放置或移除皇后，string提供了方便的索引操作来实现这个功能。相比之下，如果用vector<vector<int>>，则需要额外的代码来维护一个位置是否有皇后。
• 题目要求返回所有可能的棋盘布局，vector<string>能够直接作为结果返回，而如果是vector<vector<int>>，则需要额外的转换步骤。

for循环找对角线存在的皇后时，两个条件用&&连接的原因

		//45°有无元素for(int num1=row,num2=i;num1>=0&&num2>=0;num1--,num2--){//两个条件需要&&并列！if(chessBoard[num1][num2]=='Q'){return false;}}//135°有无元素for(int num1=row,num2=i;num1>=0&&num2<n;num1--,num2++){if(chessBoard[num1][num2]=='Q'){return false;}}

如果使用||（逻辑或）操作符，只要两边的条件之一为真，整个表达式就为真。这意味着即使num1或num2中的一个已经小于0（也就是已经越界了），只要另一个条件为真，循环就会继续，这可能导致访问数组时出现下标越界的错误。

合法性检查

当我们在单层递归里用了合法性检查的时候，我们必须注意进行合法性检查之后，向下递归的部分，需要在合法性通过的if语句块里进行递归！

也就是说必须要跳过不合法的情况，要么在单层搜索的时候直接用continue跳过，要么向下递归和回溯的整个部分，都在合法性通过的if语句块里执行。

一定要注意递归+回溯的部分，需要避免在非法的情况下执行。

		//单层递归for(int i=0;i<n;i++){//整个递归+回溯过程都在If语句块里面！if(isValid(chessBoard,row,i,n)==true){chessBoard[row][i]='Q';//递归,下一行遍历row+1backtracking(result,chessBoard,n,row+1);//回溯，找下一种解法chessBoard[row][i]='.'; }}

或者写成

		//单层递归for(int i=0;i<n;i++){//直接用continue跳过非法情况if(isValid(chessBoard,row,i,n)!=true){continue;}chessBoard[row][i]='Q';//递归,下一行遍历row+1backtracking(result,chessBoard,n,row+1);//回溯，找下一种解法chessBoard[row][i]='.'; }