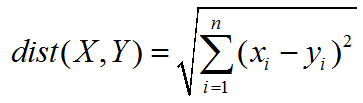最近在利用Error-Correcting Output Codes做论文，发现网上没有一种讲的比较清楚的，那我今天就花点时间大致上讲一下这种方法。最初提出ECOC方法的是如下的文章

Solving Multiclass Learning Problems via Error-Correcting Output Codes --Thomas G. Dietterich, Ghulum Bakiri

ECOC与One-vs-One(OvO)和One-vs-ALL(OvA)一样属于将多分类分解为二分类问题的分而治之（Divide and Conquer）的方法，并且也可以将ECOC理解为一种OvO和OvA经过推广过后的方法。我这里引用下面文章中的例子来说明这个问题

Reducing Multiclass to Binary: A Unifying Approach for Margin Classifiers --Erin L. Allwein, Robert E. Schapire,
Yoram Singe

1. 问题描述

给定：

1. 多分类数据
   例如：预测孩子们最喜欢的颜色
   

2. 二分类学习算法 A
   

目标： 利用二分类学习算法构建对于多分类数据的分类器

2. 一对多方法（OvA）

2.1 分解问题

将一个k-分类问题分解为k个二分类问题并且分别解决他们

2.2 怎样结合预测结果

• 一列一列评估，并且希望只有一个是 +
• 例如如果$h_1(x)=h_2(x)=h_4(x)=-$ 并且$h_3(x)=+$然后预测为 红色

2.3 问题

如果仅有一个$h$是错的，最终的预测结果就会出错

3.一对一方法（OvO）

3.1 分解问题

为每一对类别创造一个二分类器

3.2 预测阶段：

一种方法是可以利用voting的方法。即分别用这些分类器预测，计算每个种类的得票数，最终选取得票数最高的

3.3 问题和优点：

• 在预测阶段如何结合所有分类器的结果不是很显著的
• 可以达到很高的精度，训练速度甚至快于OvA方法

4. 纠错输出编码（ECOC）

4.1分解问题

1. 设计编码矩阵（“Coding” Matrix）M，并且根据M分解为若干个二分类问题（二分类问题的个数$d$ 事实上等于M的长度）

设计的方法是值得研究的话题，有文章表明是一个NP难问题。在最初的文章中作者给了几种方法；例如k不大的时候可以使用穷举编码，在k大的时候可以使用随机编码等；并且分类器个数 = 矩阵长度$d$满足
$$lo{g}_{2}k\le L\le 2^{k-1}-1,L\in \mathbb{Z}$$
最短是最少的二分类问题个数，是对数数量级的。最多的情况是穷举，是指数数量级的

3. M的每行为这个类别的编码
   例如绿色的编码为$(+,-,+,-,+)$
   

4.2 预测阶段

计算hamming distance，每个预测值也有相应的五位编码，分别与每一类的编码比对，有几位不一样hamming distance就是几，最小的那一类就是我们的预测值（最相似的一行）。

• 例如 $\mathbf{h}(x)=<-,+,+,+,->$然后预测为蓝色（hamming distance 分别为（绿色：4 黄色：2 红色：3 蓝色：1））
  

4.3 问题和优点

• 如果M的行与行差别很大，那么对错误就会有很高的鲁棒性。如果任意两行之间最小的距离是$L$，可以容忍的错误是$\frac{L-1}{2}$向下取整，仍然可以保证正确的类是最小的Hamming距离
• 在类别数k大的时候可能运行的更快
• 缺点：二分类问题不是很自然并且难以解决

4.4 推广方法

4.4.1 分解问题

M可以由 { − 1 , 0 , + 1 } \{-1, 0, +1\} {−1,0,+1}构成，其中0表示在这个二分类问题中该类不予考虑。

4.4.2 推广方法的预测阶段

4.4.3 问题及优势

因此上面的三种都可以用这种矩阵方法表示，在矩阵的选择上有一些平衡，比如

• 增加0会使得问题趋向于简单和快速训练，但是会增加二分类器的训练误差
• 行之间差距大会使得分类器鲁棒性更高，但是会导致二分类问题变得更加难以解决

5. 预测阶段

上面的方法是基于Voting或者是Hamming Distance 的，一种推广的decoding方法可以基于边际差距（Margin-based）或者说是Loss-based。