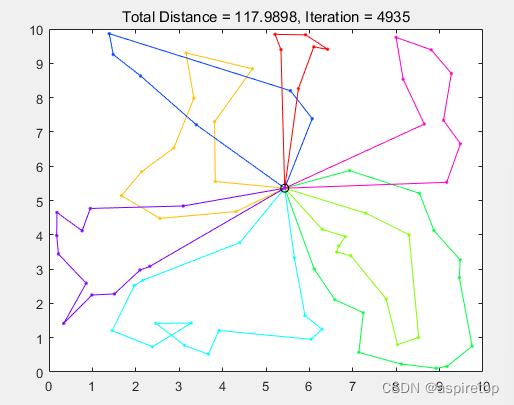
matlab2016b可运行，输入城市位置，可以动态显示规划过程 

 

% MTSPF_GA Fixed Multiple Traveling Salesmen Problem (M-TSP) Genetic Algorithm (GA)
%   Finds a (near) optimal solution to a variation of the M-TSP by setting
%   up a GA to search for the shortest route (least distance needed for
%   each salesman to travel from the start location to individual cities
%   and back to the original starting place)
%
% Summary:
%     1. Each salesman starts at the first point, and ends at the first
%        point, but travels to a unique set of cities in between
%     2. Except for the first, each city is visited by exactly one salesman
%
% Note: The Fixed Start/End location is taken to be the first XY point
%
% Input:
%     USERCONFIG (structure) with zero or more of the following fields:
%     - XY (float) is an Nx2 matrix of city locations, where N is the number of cities
%     - DMAT (float) is an NxN matrix of city-to-city distances or costs
%     - NSALESMEN (scalar integer) is the number of salesmen to visit the cities
%     - MINTOUR (scalar integer) is the minimum tour length for any of the
%         salesmen, NOT including the start/end point
%     - POPSIZE (scalar integer) is the size of the population (should be divisible by 8)
%     - NUMITER (scalar integer) is the number of desired iterations for the algorithm to run
%     - SHOWPROG (scalar logical) shows the GA progress if true
%     - SHOWRESULT (scalar logical) shows the GA results if true
%     - SHOWWAITBAR (scalar logical) shows a waitbar if true
%
% Input Notes:
%     1. Rather than passing in a structure containing these fields, any/all of
%        these inputs can be passed in as parameter/value pairs in any order instead.
%     2. Field/parameter names are case insensitive but must match exactly otherwise.
%
% Output:
%     RESULTSTRUCT (structure) with the following fields:
%         (in addition to a record of the algorithm configuration)
%     - OPTROUTE (integer array) is the best route found by the algorithm
%     - OPTBREAK (integer array) is the list of route break points (these specify the indices
%         into the route used to obtain the individual salesman routes)
%     - MINDIST (scalar float) is the total distance traveled by the salesmen
%
% Route/Breakpoint Details:
%     If there are 10 cities and 3 salesmen, a possible route/break
%     combination might be: rte = [5 6 9 4 2 8 10 3 7], brks = [3 7]
%     Taken together, these represent the solution [1 5 6 9 1][1 4 2 8 10 1][1 3 7 1],
%     which designates the routes for the 3 salesmen as follows:
%         . Salesman 1 travels from city 1 to 5 to 6 to 9 and back to 1
%         . Salesman 2 travels from city 1 to 4 to 2 to 8 to 10 and back to 1
%         . Salesman 3 travels from city 1 to 3 to 7 and back to 1
%
% Usage:
%     mtspf_ga
%       -or-
%     mtspf_ga(userConfig)
%       -or-
%     resultStruct = mtspf_ga;
%       -or-
%     resultStruct = mtspf_ga(userConfig);
%       -or-
%     [...] = mtspf_ga('Param1',Value1,'Param2',Value2, ...);
%
% Example:
%     % Let the function create an example problem to solve
%     mtspf_ga;
%
% Example:
%     % Request the output structure from the solver
%     resultStruct = mtspf_ga;
%
% Example:
%     % Pass a random set of user-defined XY points to the solver
%     userConfig = struct('xy',10*rand(35,2));
%     resultStruct = mtspf_ga(userConfig);
%
% Example:
%     % Pass a more interesting set of XY points to the solver
%     n = 50;
%     phi = (sqrt(5)-1)/2;
%     theta = 2*pi*phi*(0:n-1);
%     rho = (1:n).^phi;
%     [x,y] = pol2cart(theta(:),rho(:));
%     xy = 10*([x y]-min([x;y]))/(max([x;y])-min([x;y]));
%     userConfig = struct('xy',xy);
%     resultStruct = mtspf_ga(userConfig);
%
% Example:
%     % Pass a random set of 3D (XYZ) points to the solver
%     xyz = 10*rand(35,3);
%     userConfig = struct('xy',xyz);
%     resultStruct = mtspf_ga(userConfig);
%
% Example:
%     % Change the defaults for GA population size and number of iterations
%     userConfig = struct('popSize',200,'numIter',1e4);
%     resultStruct = mtspf_ga(userConfig);
%
% Example:
%     % Turn off the plots but show a waitbar
%     userConfig = struct('showProg',false,'showResult',false,'showWaitbar',true);
%     resultStruct = mtspf_ga(userConfig);
%
% See also: mtsp_ga, mtspo_ga, mtspof_ga, mtspofs_ga, mtspv_ga, distmat
%
% Author: Joseph Kirk
% Email: jdkirk630@gmail.com
% Release: 2.0
% Release Date: 05/01/2014
function varargout = mtspf_ga(varargin)% Initialize default configurationdefaultConfig.xy          = 10*rand(80,2)defaultConfig.dmat        = [];  % N*N距离矩阵defaultConfig.nSalesmen   = 8;defaultConfig.minTour     = 3;defaultConfig.popSize     = 80;defaultConfig.numIter     = 5e3;defaultConfig.showProg    = true;defaultConfig.showResult  = true;defaultConfig.showWaitbar = false;% Interpret user configuration inputsif ~narginuserConfig = struct();elseif isstruct(varargin{1})userConfig = varargin{1};elsetryuserConfig = struct(varargin{:});catcherror('Expected inputs are either a structure or parameter/value pairs');endend% Override default configuration with user inputsconfigStruct = get_config(defaultConfig,userConfig);% Extract configurationxy          = configStruct.xy;dmat        = configStruct.dmat;nSalesmen   = configStruct.nSalesmen;minTour     = configStruct.minTour;popSize     = configStruct.popSize;numIter     = configStruct.numIter;showProg    = configStruct.showProg;showResult  = configStruct.showResult;showWaitbar = configStruct.showWaitbar;if isempty(dmat)nPoints = size(xy,1);a = meshgrid(1:nPoints);dmat = reshape(sqrt(sum((xy(a,:)-xy(a',:)).^2,2)),nPoints,nPoints);end% Verify Inputs 验证输入[N,dims] = size(xy);[nr,nc] = size(dmat);if N ~= nr || N ~= ncerror('Invalid XY or DMAT inputs!')endn = N - 1; % Separate Start/End City% Sanity ChecksnSalesmen   = max(1,min(n,round(real(nSalesmen(1)))));minTour     = max(1,min(floor(n/nSalesmen),round(real(minTour(1)))));popSize     = max(8,8*ceil(popSize(1)/8));numIter     = max(1,round(real(numIter(1))));showProg    = logical(showProg(1));showResult  = logical(showResult(1));showWaitbar = logical(showWaitbar(1));% Initializations for Route Break Point Selection 路径断点选择的初始化nBreaks = nSalesmen-1;dof = n - minTour*nSalesmen;          % degrees of freedomaddto = ones(1,dof+1);for k = 2:nBreaksaddto = cumsum(addto);endcumProb = cumsum(addto)/sum(addto);% Initialize the PopulationspopRoute = zeros(popSize,n);         % population of routespopBreak = zeros(popSize,nBreaks);   % population of breakspopRoute(1,:) = (1:n) + 1;popBreak(1,:) = rand_breaks();for k = 2:popSizepopRoute(k,:) = randperm(n) + 1;popBreak(k,:) = rand_breaks();end% Select the Colors for the Plotted Routes    所画路径的颜色pclr = ~get(0,'DefaultAxesColor');clr = [1 0 0; 0 0 1; 0.67 0 1; 0 1 0; 1 0.5 0];if nSalesmen > 5clr = hsv(nSalesmen);end% Run the GAglobalMin = Inf;totalDist = zeros(1,popSize);distHistory = zeros(1,numIter);tmpPopRoute = zeros(8,n);tmpPopBreak = zeros(8,nBreaks);newPopRoute = zeros(popSize,n);newPopBreak = zeros(popSize,nBreaks);if showProgfigure('Name','MTSPF_GA | Current Best Solution','Numbertitle','off');hAx = gca;endif showWaitbarhWait = waitbar(0,'Searching for near-optimal solution ...');endfor iter = 1:numIter% Evaluate Members of the Population    人口评估for p = 1:popSized = 0;pRoute = popRoute(p,:);pBreak = popBreak(p,:);rng = [[1 pBreak+1];[pBreak n]]';for s = 1:nSalesmend = d + dmat(1,pRoute(rng(s,1))); % Add Start Distancefor k = rng(s,1):rng(s,2)-1d = d + dmat(pRoute(k),pRoute(k+1));endd = d + dmat(pRoute(rng(s,2)),1); % Add End DistanceendtotalDist(p) = d;end% Find the Best Route in the Population[minDist,index] = min(totalDist);distHistory(iter) = minDist;if minDist < globalMinglobalMin = minDist;optRoute = popRoute(index,:);optBreak = popBreak(index,:);rng = [[1 optBreak+1];[optBreak n]]';if showProg% Plot the Best Route   实时展示最优路径for s = 1:nSalesmenrte = [1 optRoute(rng(s,1):rng(s,2)) 1];if dims > 2, plot3(hAx,xy(rte,1),xy(rte,2),xy(rte,3),'.-','Color',clr(s,:));else plot(hAx,xy(rte,1),xy(rte,2),'.-','Color',clr(s,:)); endhold(hAx,'on');endif dims > 2, plot3(hAx,xy(1,1),xy(1,2),xy(1,3),'o','Color',pclr);else plot(hAx,xy(1,1),xy(1,2),'o','Color',pclr); endtitle(hAx,sprintf('Total Distance = %1.4f, Iteration = %d',minDist,iter));hold(hAx,'off');drawnow;endend% Genetic Algorithm OperatorsrandomOrder = randperm(popSize);for p = 8:8:popSizertes = popRoute(randomOrder(p-7:p),:);brks = popBreak(randomOrder(p-7:p),:);dists = totalDist(randomOrder(p-7:p));[ignore,idx] = min(dists); %#okbestOf8Route = rtes(idx,:);bestOf8Break = brks(idx,:);routeInsertionPoints = sort(ceil(n*rand(1,2)));I = routeInsertionPoints(1);J = routeInsertionPoints(2);for k = 1:8 % Generate New SolutionstmpPopRoute(k,:) = bestOf8Route;tmpPopBreak(k,:) = bestOf8Break;switch kcase 2 % FliptmpPopRoute(k,I:J) = tmpPopRoute(k,J:-1:I);case 3 % SwaptmpPopRoute(k,[I J]) = tmpPopRoute(k,[J I]);case 4 % SlidetmpPopRoute(k,I:J) = tmpPopRoute(k,[I+1:J I]);case 5 % Modify BreakstmpPopBreak(k,:) = rand_breaks();case 6 % Flip, Modify BreakstmpPopRoute(k,I:J) = tmpPopRoute(k,J:-1:I);tmpPopBreak(k,:) = rand_breaks();case 7 % Swap, Modify BreakstmpPopRoute(k,[I J]) = tmpPopRoute(k,[J I]);tmpPopBreak(k,:) = rand_breaks();case 8 % Slide, Modify BreakstmpPopRoute(k,I:J) = tmpPopRoute(k,[I+1:J I]);tmpPopBreak(k,:) = rand_breaks();otherwise % Do NothingendendnewPopRoute(p-7:p,:) = tmpPopRoute;newPopBreak(p-7:p,:) = tmpPopBreak;endpopRoute = newPopRoute;popBreak = newPopBreak;% Update the waitbarif showWaitbar && ~mod(iter,ceil(numIter/325))waitbar(iter/numIter,hWait);endendif showWaitbarclose(hWait);endif showResult% Plots     画图figure('Name','MTSPF_GA | Results','Numbertitle','off');subplot(2,2,1);if dims > 2, plot3(xy(:,1),xy(:,2),xy(:,3),'.','Color',pclr);else plot(xy(:,1),xy(:,2),'.','Color',pclr); endtitle('City Locations');subplot(2,2,2);imagesc(dmat([1 optRoute],[1 optRoute]));title('Distance Matrix');subplot(2,2,3);rng = [[1 optBreak+1];[optBreak n]]';for s = 1:nSalesmenrte = [1 optRoute(rng(s,1):rng(s,2)) 1];if dims > 2, plot3(xy(rte,1),xy(rte,2),xy(rte,3),'.-','Color',clr(s,:));else plot(xy(rte,1),xy(rte,2),'.-','Color',clr(s,:)); endtitle(sprintf('Total Distance = %1.4f',minDist));hold on;endif dims > 2, plot3(xy(1,1),xy(1,2),xy(1,3),'o','Color',pclr);else plot(xy(1,1),xy(1,2),'o','Color',pclr); endsubplot(2,2,4);plot(distHistory,'b','LineWidth',2);title('Best Solution History');set(gca,'XLim',[0 numIter+1],'YLim',[0 1.1*max([1 distHistory])]);end% Return Outputif nargoutresultStruct = struct( ...'xy',          xy, ...'dmat',        dmat, ...'nSalesmen',   nSalesmen, ...'minTour',     minTour, ...'popSize',     popSize, ...'numIter',     numIter, ...'showProg',    showProg, ...'showResult',  showResult, ...'showWaitbar', showWaitbar, ...'optRoute',    optRoute, ...'optBreak',    optBreak, ...'minDist',     minDist);varargout = {resultStruct};end% Generate Random Set of Break Pointsfunction breaks = rand_breaks()if minTour == 1 % No Constraints on BreakstmpBreaks = randperm(n-1);breaks = sort(tmpBreaks(1:nBreaks));else % Force Breaks to be at Least the Minimum Tour LengthnAdjust = find(rand < cumProb,1)-1;spaces = ceil(nBreaks*rand(1,nAdjust));adjust = zeros(1,nBreaks);for kk = 1:nBreaksadjust(kk) = sum(spaces == kk);endbreaks = minTour*(1:nBreaks) + cumsum(adjust);endendend% Subfunction to override the default configuration with user inputs
% 将输入初始化，什么都不输入，就用这个应该是
function config = get_config(defaultConfig,userConfig)% Initialize the configuration structure as the defaultconfig = defaultConfig;% Extract the field names of the default configuration structuredefaultFields = fieldnames(defaultConfig);% Extract the field names of the user configuration structureuserFields = fieldnames(userConfig);nUserFields = length(userFields);% Override any default configuration fields with user valuesfor i = 1:nUserFieldsuserField = userFields{i};isField = strcmpi(defaultFields,userField);if nnz(isField) == 1thisField = defaultFields{isField};config.(thisField) = userConfig.(userField);endendend