• 题意：You are given a sequence a consisting of $n$ integers. Find the maximum possible value of (integer remainder of $a_i$ divided by $a_j$), where $1\le i,j\le n$ and $a_i\ge a_j$.
• 看清，限制条件是 $a_i\ge a_j$.
• 其实就是从 $2\ast a$ 到 $2\ast ma{x}_a$，每次增加 $a$，找到小于 $k\ast a$ 的最大值，答案就在这些之中。
• 还有一个 $O(1)$ 的做法找到小于 $k\ast a$ 的方法，看看这个，脑洞还挺大的。

#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn = 2000010;
int A[maxn], B[maxn], N;
int main() {scanf("%d", &N);for (int i = 0; i < N; i++) {int x;scanf("%d", &x);A[x] = x;}for (int i = 1; i <= 2000000; i++) {B[i] = max(A[i], B[i - 1]);}int ans = 0;for (int i = 1; i <= 1000000; i++) {if (A[i]) {for (int j = 2 * i; j <= 2000000; j += i)  ans = max(ans, B[j - 1] % i);}}printf("%d\n", ans);
}

• lower_bound()返回一个 iterator 它指向在[first,last)标记的有序序列中可以插入value，而不会破坏容器顺序的第一个位置，而这个位置标记了一个不小于value 的值。如果最后一个数比value还小就返回last。
• 二分的方法，我的超时了，就是说 $O(N\ast logN\ast logM)$ 的方法不行。

• 题意：给一个数组，一段区间，问在区间中有多少个数字，是区间内所有数字的因数？
• 想了想，其实用线段树很简单就能实现。每次只用看一段区间的最小值，以及最小值是否和这段区间的最大公约数相等，再存一下这段区间的最小值有几个。
• 我发现，似乎线段树的题目，令query()函数都是返回node，这样子似乎可以解决一切问题，就算板子中有的query()函数是返回一个值，也可以改成返回node的板子。

#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long ll;
const int maxn = 100010;
int N, T;
ll a[maxn];
struct node {int l, r;ll d, minimum, nums;
}tr[maxn * 4];
ll gcd(ll a, ll b) {if (b == 0) return a;return gcd(b, a % b);
}
void pushup(node& u, node& l, node& r) {u.d = gcd(l.d, r.d);if (l.minimum < r.minimum) {u.minimum = l.minimum;u.nums = l.nums;}else if (l.minimum > r.minimum) {u.minimum = r.minimum;u.nums = r.nums;}else {u.minimum = l.minimum;u.nums = l.nums + r.nums;}
}
void pushup(int u) {pushup(tr[u], tr[2 * u], tr[2 * u + 1]);
}
void build(int u, int l, int r) {if (l == r) tr[u] = { l, r, a[l], a[l], 1 };else {tr[u].l = l, tr[u].r = r;int mid = (l + r) / 2;build(2 * u, l, mid), build(2 * u + 1, mid + 1, r);pushup(u);}
}
node query(int u, int l, int r) {if (l <= tr[u].l && tr[u].r <= r) return tr[u];int mid = (tr[u].l + tr[u].r) / 2;if (r <= mid) return query(2 * u, l, r);else if (l > mid) return query(2 * u + 1, l, r);else {node left = query(2 * u, l, r);node right = query(2 * u + 1, l, r);node res;pushup(res, left, right);return res;}
}
int main() {scanf("%d", &N);for (int i = 1; i <= N; i++) scanf("%lld", &a[i]);build(1, 1, N);scanf("%d", &T);while (T--) {int l, r;scanf("%d%d", &l, &r);node res = query(1, l, r);if (res.d == res.minimum) {printf("%lld\n", r - l + 1 - res.nums);}else {printf("%d\n", r - l + 1);}}return 0;
}

• 两个区间集和，各有n个区间，第一个区间集和初始都为 $[l1,r1]$，第二个区间集和初始都为 $[l2,r2]$。一次操作可以将区间 $[x,y]$ 变成 $[x-1,y]$ 或者 $[x,y+1]$。求区间交集长度之和为 $k$ 的最少操作次数。
• 这个看上去情况很多，但是不要忘记n的范围很小，因此可以考虑暴力枚举的方式。主要是一个地方容易出现讨论，就是说，是先让下一对区间有交集，还是扩展上一个区间？
• 我们可以换个思路讨论。枚举需要扩展的区间，从1枚举到n，然后就很好写了。

#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
ll N, K, T, l1, l2, r1, r2;
int main() {cin >> T;while (T--) {cin >> N >> K >> l1 >> r1 >> l2 >> r2;ll ans = 1e18;ll lmax = max(l1, l2), rmax = max(r1, r2), lmin = min(l1, l2), rmin = min(r1, r2);K -= N * max(rmin - lmax, 0LL);if (K <= 0) ans = 0;else for (ll x = 1; x <= N; x++) {ll res = x * max(lmax - rmin, 0LL), max_get = x * (rmax - lmin - max(rmin - lmax, 0LL));if (max_get >= K) {res += K;}else {res += max_get + (K - max_get) * 2;}ans = min(ans, res);}cout << ans << endl;}
}

• 我发现最近经常碰到这种题这种题，特点就是分类讨论的话情况异常复杂，但是题解又是一种略带暴力的感觉就搜索到了所有情况，而且自己一般都不怎么想得出来。
• 题意：对于高度数组a[],目的是将所有高度平齐，有三种操作：1、a[i]–代价为R；2、a[i]++代价为A；3、将某一位置的一个单位转移到另一个位置 代价为M，问最小代价能平齐的高度；
• 三分搜索出答案。

#include<iostream>
#include<algorithm>
using namespace std;
const int maxn = 100010;
int N, a[maxn];
typedef long long ll;
ll A, R, M;
ll f(ll x) {ll lower = 0, upper = 0, res = 0;for (int i = 1; i <= N; i++) {if (a[i] > x) upper += a[i] - x;else lower += x - a[i];}if (M < A + R) {ll move = min(lower, upper);res += M * move;upper -= move, lower -= move;}res += A * lower + R * upper;return res;
}
int main() {cin >> N >> A >> R >> M;for (int i = 1; i <= N; i++) cin >> a[i];ll lb = 0, ub = 1e9 + 5;while (ub - lb > 1) {ll m1 = (lb + ub) / 2;ll m2 = (m1 + ub) / 2;ll f1 = f(m1), f2 = f(m2);if (f1 > f2) lb = m1;else ub = m2;}cout << min(f(lb), f(ub)) << endl;return 0;
}

• 题意：通过查询构造出答案要求的密码，每次查询可以询问数组A中指定的集合的最大值，最多可以查询12次，我们要构造的密码序列，对于一个密码Pi， Pi为除了Si这个集合中索引对应的数组A中的数字的最大值，Si是k个互不独立的集合。
• 二分的次数一定要估算准确！用公式！$\lceil lo{g}_{2}N\rceil .$
• 交互题果然好多都是二分查找。
• 前十次，找出最大值所在的位置。第十一次，问最大值所在的那个集合的最大值。第十二次，问上述集合的补集的最大值。这样子答案是不是就出来了！
• 我其实不太知道自己哪里写错了，但是这个二分写的异常复杂！但是网上的二分搜索写的就非常简单，因为他们是 $[1,k]$ 之间定位最大值，用 lb 和 ub 去卡最大值，最后卡到数组的最后一个位置便是最大值的位置。
• 这个确实有点裂开，他的输入有坑！可能不会把所有的集合的信息都给你，因为他认为给你k-1个集合就可以知道k个集合的信息了！我居然在这个地方错了一个小时！我还是一行一行对别人的代码才发现的这个问题！
• 不过还是有收获的。最起码今天看到了交互题用二分去写的一个清爽的思路，之前那种讨论方式确实不可取。以及正数二分的一个新的写法，好像这种写法挺好用的。

#include<iostream>
#include<algorithm>
#include<vector>
#include<string>
#include<cstdio>
#include<cstring>
using namespace std;
const int maxn = 1010;
int belong[maxn], N, K, sz[maxn], ans[maxn];
string result;
int query(vector<int>& v) {printf("? %d", v.size());for (auto u : v) {printf(" %d", u);}printf("\n");fflush(stdout);int x;cin >> x;return x;
}
int main() {int T;cin >> T;while (T--) {cin >> N >> K;vector<int> q;memset(belong, 0, sizeof belong);for (int i = 1; i <= K; i++) {int C;cin >> C;sz[i] = C;for (int j = 1; j <= C; j++) {int idx;cin >> idx;belong[idx] = i;}}for (int i = 1; i <= N; i++) q.push_back(i);int mx = query(q);int lb = 1, ub = N;while (ub - lb >= 1) {int mid = (lb + ub) / 2;q.clear();for (int i = 1; i <= mid; i++) q.push_back(i);int xx = query(q);if (xx < mx) lb = mid + 1;else ub = mid;}int set_id = belong[lb];for (int i = 1; i < set_id; i++) ans[i] = mx;for (int i = set_id + 1; i <= K; i++) ans[i] = mx;q.clear();for (int i = 1; i <= N; i++) {if (belong[i] != set_id) q.push_back(i);}ans[set_id] = query(q);printf("! ");for (int i = 1; i <= K; i++) {printf("%d%c", ans[i], i == K ? '\n' : ' ');}fflush(stdout);cin >> result;if (result != "Correct") break;}return 0;
}
/*
3
4 2
2 1 3
2 2 4
4
2
3
3
Correct2 2
1 1
1 2
2
1
1
Correct3 2
1 1
2 2 3
3
2
3
1
Correct
*/

• 题意：给定一个数列：$a_1,a_2,...,a_n$。定义 $K_a$ 为区间 $[l，r]$ 中 $a$ 出现的次数。$t$ 个查询，每个查询l，r，对区间内所有 $a[i]$ ，求 $\sum K^2\ast a[i]$
• 用到了莫队算法：离线+分块。将n个数分成sqrt(n)块。对所有询问进行排序，排序标准：

1. Q[i].left /block_size < Q[j].left / block_size （块号优先排序）
2. 如果1相同，则 Q[i].right < Q[j].right （按照查询的右边界排序）

• 如果一个数已经出现了x次，那么需要累加 $(2\ast x+1)\ast a[i]$，因为 $(x+1{)}^2\ast a[i]=(x^2+2\ast x+1)\ast a[i]$，$x^2\ast a[i]$ 是出现x次的结果，$(x+1{)}^2\ast a[i]$ 是出现x+1次的结果。
• 看了代码之后，妙啊！

#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
const int maxa = 1000010, maxn = 200010;
typedef long long ll;
struct query {int l, r, id;
}Q[maxn];//sum[i] 是当前查到的 i 这个数字有多少个。
ll a[maxn], sum[maxa], ans[maxn];
int N, T, block_size, L, R;  //当前的左边界、右边界。
ll now;  //当前的答案bool cmp(query a, query b) {if (a.l / block_size == b.l / block_size) return a.r < b.r;return a.l / block_size < b.l / block_size;
}void modify(int l, int r) {//若当前 L 在 l 的左边while (L < l) {now -= (2 * sum[a[L]] - 1) * a[L];sum[a[L]]--;L++;}//若当前 L 在 l 的右边while (L > l) {L--;now += (2 * sum[a[L]] + 1) * a[L];sum[a[L]]++;}//若当前 R 在 r 的左边while (R < r) {R++;now += (2 * sum[a[R]] + 1) * a[R];sum[a[R]]++;}//若当前 R 在 r 的右边while (R > r) {now -= (2 * sum[a[R]] - 1) * a[R];sum[a[R]]--;R--;}
}
int main() {scanf("%d%d", &N, &T);for (int i = 1; i <= N; i++) scanf("%I64d", &a[i]);for (int i = 1; i <= T; i++) {scanf("%d%d", &Q[i].l, &Q[i].r);Q[i].id = i;}block_size = sqrt(N);sort(Q + 1, Q + T + 1, cmp);for (int i = 1; i <= T; i++) {modify(Q[i].l, Q[i].r);ans[Q[i].id] = now;}for (int i = 1; i <= T; i++) {printf("%I64d\n", ans[i]);}return 0;
}

• 题意：给出一个h*w的棋盘(h,w<=1e5),其中有n个位置不能走(n<=2000),现在要从左上角走到右下角，每步只能向下或者向右走一步。问有多少种走法？右下角保证可以走到。
• Let’s denote black cells as $A_0,A_1,...,A_{k-1}$. First of all, we have to sort black cells in increasing order of (row, column). If cell x available from cell y, x stands after y in this order. Let Ak = (h, w). Now we have to find number of paths from (1, 1) to $A_k$ avoiding $A_0,...,A_{k-1}$.
• 对于 $A_i$，从 $(1,1)$ 走到 $(x_i,y_i)$ 且绕开前方所有黑格子的方法数目为 $dp(i)$, 那么找到所有能到 $A_i$ 的节点（比如 $(x_j,y_j)$），把这个 $dp(i)$ 减掉 $dp(j)$ 与 从 $A_j$ 到 $A_j$ 的所有路径就好。设 $dp(i)$ 为到达 $A_i$ 的不合法路径总数。
• 最后那个乘积道的理很简单，因为后面的那个从 $A_j$ 到 $A_i$ 的全部路径，乘上躲开前方所有黑色节点的路径，其实已经是经过 $A_i$ 的不经过前方所有黑色节点的不合法路径了，这样就把所有不合法路径不重不漏的找到了。
• 注意，前k个节点，是寻找的走到黑格子的方案数，所以是不合法路径的数目。但是最后一个格子是目标点，此时的 dp(i) 是合法路径的数量呀。
• 最后发现傻掉了。数组要开到200010，因为会计算 $C(N+M-2,N-1)$.

#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
typedef long long ll;
const ll mod = 1e9 + 7;
const int maxn = 2010;
ll dp[maxn], fact[200010] = { 1 }, infact[200010] = { 1 };
typedef pair<int, int> P;
vector<P> black;
ll N, M, T;
ll mod_pow(ll x, ll n) {ll res = 1;while (n) {if (n & 1) res = res * x % mod;x = x * x % mod;n >>= 1;}return res;
}
ll C(ll M, ll N) {return fact[M] * infact[N] % mod * infact[M - N] % mod;
}
int main() {cin >> N >> M >> T;for (ll i = 1; i <= 200000; i++) {fact[i] = fact[i - 1] * i % mod;infact[i] = infact[i - 1] * mod_pow(i, mod - 2) % mod;}for (int i = 0; i < T; i++) {int x, y;cin >> x >> y;black.push_back(P(x, y));}black.push_back(P(N, M));sort(black.begin(), black.end());for (int i = 0; i < black.size(); i++) {int xi = black[i].first, yi = black[i].second;dp[i] = C((ll)xi + yi - 2, (ll)xi - 1);for (int j = 0; j < i; j++) {int xj = black[j].first, yj = black[j].second;if (yj > yi) continue;dp[i] = (dp[i] - dp[j] * C((ll)xi + yi - xj - yj, (ll)xi - xj) % mod + mod) % mod;}}cout << dp[T] << endl;return 0;
}

• 题意：在1~n的n个数中，对于k∈[2,n]，在n个数中取k个数，对这k个数两两进行gcd，输出这个gcd最小的最大值。
• 思路：因为要求gcd，我们肯定要先把素数（还有1）一个一个放进去。当素数放完之后，我们接下来放的数字一定会是当前集合某个数的倍数。那么我们要让这个数字尽可能地小。于是，我们按照最大非自身地因子尽可能地小，往里面填放，就可以得到最优解。因此，把最大公因子从小到大排序，然后输出第2~第n小的数字即可。

#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn = 500010;
int prime[maxn], st[maxn], cnt;
void sieve(int N) {st[1] = 1;for (int i = 2; i <= N; i++) {if (!st[i]) prime[cnt++] = st[i] = i;for (int j = 0; prime[j] <= N / i; j++) {st[prime[j] * i] = prime[j];if (i % prime[j] == 0) break;}}
}
int main() {sieve(maxn - 1);int N;scanf("%d", &N);for (int i = 1; i <= N; i++) {st[i] = i / st[i];}sort(st + 1, st + N + 1);for (int i = 2; i <= N; i++) {printf("%d%c", st[i], i == N ? '\n' : ' ');}return 0;
}

• 给出a数组,b数组,下标为2~n-1 可以进行操作,a[i]=a[i+1]+a[i-1]-a[i],问进行若干次操作,能否将a数组变成b数组。
• Consider the difference array $d_1,d_2,\dots ,d_{n-1},$ where $d_i=c_{i+1}-c_i.$ Let’s see what happens if we apply synchronization.
• Pick an arbitrary index $j$ and transform $c_j$ to $c_j^{\prime }=c_{j+1}+c_{j-1}-c_j.$ Then:
• $d_{j-1}^{\prime }=c_j^{\prime }-c_{j-1}=(c_{j+1}+c_{j-1}-c_j)-c_{j-1}=c_{j+1}-c_j=d_j$
• $d_j^{\prime }=c_{j+1}-c_j^{\prime }=c_{j+1}-(c_{j+1}+c_{j-1}-c_j)=c_j-c_{j-1}=d_{j-1}$
• 新奇，居然就是差分数组的交换。看看两个差分数组的前n-1项是否是一样的map就行。
• 如果两个数组的差分数组一样，那么这两个数组就是一样的（因为前缀和一样啊）。

#include<cstdio>
#include<algorithm>
#include<unordered_map>
using namespace std;
const int maxn = 100010;
typedef long long ll;
ll c[maxn], t[maxn], c_d[maxn], t_d[maxn];
unordered_map<ll, ll> c_map, t_map;
int N;
int main() {scanf("%d", &N);for (int i = 1; i <= N; i++) scanf("%lld", &c[i]);for (int i = 1; i <= N; i++) scanf("%lld", &t[i]);for (int i = 1; i <= N; i++) c_d[i] = c[i] - c[i - 1], t_d[i] = t[i] - t[i - 1];for (int i = 1; i <= N; i++) c_map[c_d[i]]++, t_map[t_d[i]]++;bool flag = (c[1] == t[1] && c[N] == t[N]);for (auto p : c_map) {int u = p.first, cnt = p.second;if (t_map[u] != cnt) {flag = false;break;}}if (flag) printf("Yes\n");else printf("No\n");return 0;
}

• 很简单的一道题，不多说了，就是会爆 long long。网上有人使用long double写的。高精度写起来的好麻烦的，还要判断正负号。所以还是用 long double 吧。
• long double 用 %.Lf 输出。注意L要大写。

#include<cstdio>
#include<algorithm>
#include<unordered_map>
#include<vector>
using namespace std;
const int maxn = 200010;
int N;
typedef long long ll;
ll a[maxn];
unordered_map<ll, ll> a_cnt;int main() {scanf("%d", &N);for (int i = 1; i <= N; i++) scanf("%lld", &a[i]);long double ans = 0;for (int i = 1; i <= N; i++) {ans += (ll)i * a[i] -((ll)N - (ll)i + 1LL) * a[i];}for (int i = 1; i <= N; i++) {a_cnt[a[i]]++;ll x = a_cnt[a[i] + 1], y = a_cnt[a[i] - 1];ans = ans + x - y;}printf("%.Lf\n", ans);return 0;
}

• 题目大意：
  给你一个序列，你要在这个序列上进行操作。
  操作1 : 给定区间 $[l,r]$，对序列中这个区间的所有数求和。
  操作2 : 给你区间 $[l,r]$ 和 x，该区间所有数对 x 取模。
  操作3 :给你两个数 $k$ 和 $x$，把 $a[k]$ 修改为 $x$。
• 1和3都是常规操作，2的话，其实只需要把当前区间的最大值m修改为 m % x，这个修改也很简单，当递归到某个区间长度为1的时候，把这个数字修改掉，然后向上pushup即可。

#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxn = 100010;
typedef long long ll;
int N, M, a[maxn];
struct node {int l, r;ll sum, m;
}tr[maxn * 4];
void pushup(node& u, node& l, node& r) {u.sum = l.sum + r.sum;u.m = max(l.m, r.m);
}
void pushup(int u) {pushup(tr[u], tr[2 * u], tr[2 * u + 1]);
}
void pushdown(int u) {auto& root = tr[u], & left = tr[2 * u], & right = tr[2 * u + 1];}
void build(int u, int l, int r) {if (l == r) tr[u] = { l, r, a[l], a[l] };else {tr[u].l = l, tr[u].r = r;int mid = (l + r) / 2;build(2 * u, l, mid), build(2 * u + 1, mid + 1, r);pushup(u);}
}
node query(int u, int l, int r) {if (l <= tr[u].l && tr[u].r <= r) return tr[u];int mid = (tr[u].l + tr[u].r) / 2;if (r <= mid) return query(2 * u, l, r);else if (l > mid) return query(2 * u + 1, l, r);else {node left = query(2 * u, l, r);node right = query(2 * u + 1, l, r);node res;pushup(res, left, right);return res;}
}
void modify(int u, int x, ll d) {if (tr[u].l == x && tr[u].r == x) tr[u] = { x, x, d, d};else {int mid = (tr[u].l + tr[u].r) / 2;if (x <= mid) modify(2 * u, x, d);else modify(2 * u + 1, x, d);pushup(u);}
}
void modify(int u, int l, int r, int x) {if (tr[u].m < x) return;if (tr[u].l == tr[u].r && tr[u].l >= l && tr[u].r <= r) {tr[u].m %= x;tr[u].sum = tr[u].m;}else {int mid = (tr[u].l + tr[u].r) / 2;if (l <= mid) modify(2 * u, l, r, x); //进入左区间if (r > mid) modify(2 * u + 1, l, r, x);  //进入右区间//else modify(2 * u, l, r, x), modify(2 * u + 1, l, r, x);  //进入两个区间pushup(u);}
}
int main() {scanf("%d%d", &N, &M);for (int i = 1; i <= N; i++) scanf("%d", &a[i]);build(1, 1, N);while (M--) {int op, l, r, x, k;scanf("%d", &op);if (op == 1) {scanf("%d%d", &l, &r);printf("%lld\n", query(1, l, r).sum);}else if (op == 2) {scanf("%d%d%d", &l, &r, &x);modify(1, l, r, x);}else {scanf("%d%d", &k, &x);modify(1, k, x);}}return 0;
}

• 题意：You are given a prime number $p,n$ integers $a_1,a_2,\dots ,a_n$, and an integer $k$.Find the number of pairs of indexes $(i,j)$ $(1\le i<j\le n)$ for which $(a_i+a_j)(a_i^2+a_j^2)\equiv kmodp$.
  
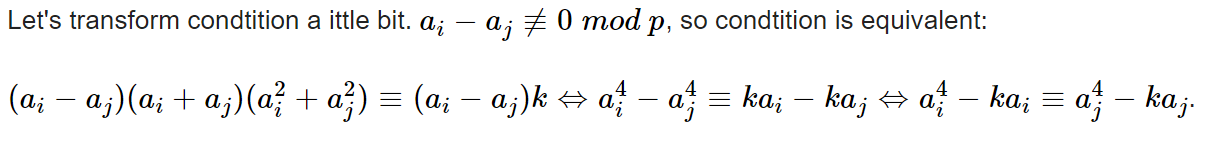
• nm，这谁能想得到。不过，我感觉，碰到这么稀奇古怪的等式，很多时候都是想办法把 $i$ 和 $j$ 弄到等号两边去。

#include<cstdio>
#include<algorithm>
#include<unordered_map>
using namespace std;
typedef long long ll;
const int maxn = 300010;
ll N, mod, K;
unordered_map<ll, ll> cnt;
ll mod_pow(ll x, ll n) {ll res = 1;while (n) {if (n & 1) res = res * x % mod;x = x * x % mod;n >>= 1;}return res;
}
int main() {scanf("%lld%lld%lld", &N, &mod, &K);for (int i = 0; i < N; i++) {ll x;scanf("%lld", &x);x = ((mod_pow(x, 4) - x * K) % mod + mod) % mod;cnt[x]++;}ll ans = 0;for (auto p : cnt) {int u = p.second;ans += u * (u - 1) / 2;}printf("%lld\n", ans);return 0;
}

• 题意很简单，给一个数组
  
• 线段树是这样存储的：叶子节点存储 { f i b ( a i ) , f i b ( a i + 1 ) } \{fib(a_i), fib(a_i+1)\} {fib(ai​),fib(ai​+1)}. 就是一个 $f$ 数组，那么非叶节点 $f$ 数组的两个分别存储两个儿子的 $f$ 的值之和。
• 那么，懒人标记怎么办呢？其实就是储存一个矩阵 $Q^x$，因为，直接用 $f$ 去乘 $Q^x$，就等价于把每个节点都加了一个数字，然后加起来。

#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxn = 100010;
typedef long long ll;
const ll mod = 1e9 + 7;
ll a[maxn];
int N, M;
const ll E[2][2] = { {1, 0}, {0, 1} };
struct node {int l, r;ll f[2], mul[2][2];
}tr[maxn * 4];
void mul(ll c[], ll a[], ll b[][2]) {ll tmp[2] = { 0 };for (int i = 0; i < 2; i++) {for (int j = 0; j < 2; j++) {tmp[i] = (tmp[i] + a[j] * b[j][i]) % mod;}}memcpy(c, tmp, sizeof tmp);
}
void mul(ll c[][2], ll a[][2], ll b[][2]) {ll tmp[2][2] = { 0 };for (int i = 0; i < 2; i++) {for (int j = 0; j < 2; j++) {for (int k = 0; k < 2; k++) {tmp[i][j] = (tmp[i][j] + a[i][k] * b[k][j]) % mod;}}}memcpy(c, tmp, sizeof tmp);
}
ll fib(ll n) {ll f[2] = { 1, 1 };ll a[2][2] = {{0, 1},{1, 1}};n -= 2;/*if (n == 0) return 1;*/while (n > 0) {if (n & 1) mul(f, f, a);mul(a, a, a);n >>= 1;}return f[1];
}
void pushup(node& u, node& l, node& r) {u.f[0] = (l.f[0] + r.f[0]) % mod;u.f[1] = (l.f[1] + r.f[1]) % mod;
}
void pushup(int u) {pushup(tr[u], tr[2 * u], tr[2 * u + 1]);
}void build(int u, int l, int r) {memcpy(tr[u].mul, E, sizeof E);if (l == r) {tr[u] = { l, l, fib(a[l]), fib(a[l] + 1) };}else {tr[u].l = l, tr[u].r = r;int mid = (l + r) / 2;build(2 * u, l, mid), build(2 * u + 1, mid + 1, r);pushup(u);}
}
void eval(node& u, ll q[][2]) {mul(u.f, u.f, q);mul(u.mul, u.mul, q);
}
void pushdown(int u) {eval(tr[2 * u], tr[u].mul);eval(tr[2 * u + 1], tr[u].mul);memcpy(tr[u].mul, E, sizeof E);
}
node query(int u, int l, int r) {if (l <= tr[u].l && tr[u].r <= r) return tr[u];pushdown(u);int mid = (tr[u].l + tr[u].r) / 2;if (r <= mid) return query(2 * u, l, r);else if (l > mid) return query(2 * u + 1, l, r);else {node left = query(2 * u, l, r);node right = query(2 * u + 1, l, r);node res;pushup(res, left, right);return res;}
}
void modify(int u, int l, int r, ll q[][2]) {if (l <= tr[u].l && tr[u].r <= r) {eval(tr[u], q);}else {pushdown(u);int mid = (tr[u].l + tr[u].r) / 2;if (l <= mid) modify(2 * u, l, r, q);if (r > mid) modify(2 * u + 1, l, r, q);pushup(u);}
}
int main() {//for (int i = 1; i <= 10; i++) printf("*** %lld\n", fib(i));scanf("%d%d", &N, &M);for (int i = 1; i <= N; i++) scanf("%lld", &a[i]);build(1, 1, N);while (M--) {int t, l, r;ll x;scanf("%d%d%d", &t, &l, &r);if (t == 1) {scanf("%lld", &x);ll res[2][2];memcpy(res, E, sizeof E);ll multi[2][2]{{0, 1},{1, 1}};while (x) {if (x & 1) mul(res, res, multi);mul(multi, multi, multi);x >>= 1;}modify(1, l, r, res);}else {printf("%lld\n", query(1, l, r).f[0]);}}return 0;
}

• 题意：n个数，q个查询操作，每次操作对第x个数进行操作，如果序列里面没有这个数，就把这个数加进去，如果有就取出来，问在序列中有多少组数，满足互质的情况。
• 其实就是一个简单的容斥原理，但是要小心1，这道题我在这个地方绊了好几下。

#include<cstdio>
#include<algorithm>
#include<unordered_map>
#include<vector>
#include<unordered_set>
using namespace std;
const int maxa = 500010, maxn = 200010;
int N, Q, a[maxn];
int prime[maxa], cnt, st[maxa];
void sieve(int N) {st[1] = 1;for (int i = 2; i <= N; i++) {if (!st[i]) st[i] = prime[cnt++] = i;for (int j = 0; prime[j] <= N / i; j++) {st[prime[j] * i] = prime[j];if (i % prime[j] == 0) break;}}
}
typedef unordered_map<int, int> um;
um now;
unordered_set<int> ss;
int divisor(int N, bool flag) {int n = N;vector<int> res;int ans = ss.size();while (N > 1) {int x = st[N];res.push_back(x);while (N % x == 0) N /= x;}int sz = res.size();for (int i = 1; i < (1 << sz); i++) {int xx = 1, cnt = 0;for (int j = 0; j < sz; j++) {if ((i >> j) & 1) {xx *= res[j];cnt++;}}if (cnt & 1) ans -= now[xx];else ans += now[xx];if (flag) now[xx]--;else now[xx]++;}if (n == 1 && flag) return -ans + 1;else if (flag) return -ans;return ans;
}typedef long long ll;int main() {scanf("%d%d", &N, &Q);for (int i = 1; i <= N; i++) scanf("%d", &a[i]);sieve(maxa - 1);ll ans = 0;while (Q--) {int x;scanf("%d", &x);ans += divisor(a[x], ss.count(x));if (ss.count(x)) ss.erase(x);else ss.insert(x);printf("%lld\n", ans);}return 0;
}

• 题意：给出n个敌人，每个敌人有 $a_i$ 个糖果，你一开始手中有 $x$ 个糖果，每次只能选择糖果数小于你当前手中糖果的敌人，战胜他并获得一颗糖果。选择敌人的顺序构成一个排列P。$f(x)$ 表示一开始有 $x$ 个糖果时，可行的排列方案数。给出一个素数 $p(p⩽n)$，求出所有满足 $f(x)modp\ne 0$ 的 x.
• 算了，这道题好恶心呀，不想写了。

• 题意：给出一个数列，每次可以选取一个区间，按顺序加上第i个菲波那契数进行更新，也可以查询某一个区间的总和。
• 斐波那契数列性质：

1. 若一个数列满足F(1)=a,F(2)=b,F(i)=F(i-2)+F(i-1)，则有F(n)=aFib(n-2)+bFib(n-1)，且F的前N项和等于F(n+2)-F(2)。这个很容易推导出来。
2. 两个菲波那契数列相加之后依旧是一个菲波那契数列，只是前两项的值变化，分别变为了两个菲波那契数列前两项的和。

• 因此，这样的类斐波那契数列，想求 $F(n)$ 的前n项和，只需要求 $F(n+2)-F(2)$
  即可。而 $F(n)=a\ast F(n-2)+b\ast F(n-1).$ $a$ 和 $b$ 分别为这个类斐波那契数列的前两项。
• 这里的懒人标记是f1, f2，表示在此节点的整个区间上面加上一个前两项是 $f1$ 和 $f2$ 的类斐波那契数列。
• 不过，我要先说一下懒人标记，这个东西别用错了。这道题在懒人标记上面错了很长时间。懒人标记是方便你往下pushdown的时候用的，有这些特点：

1. 每一次pushdown的时候，线段树节点的某些属性是要清零的。
2. 懒人标记中被清零的那些属性一般来讲与答案不会直接相关。只是为了方便修改某个与答案直接相关的属性而存在的（比如sum），而这个属性与答案是直接相关的。
3. 懒人标记是为了修改两个子节点的整个区间的，就比如这个题，f1, f2 是为了在两个子区间上面直接加上一个类斐波那契数列的一段，而这个类斐波那契数列的区间长度和对应子区间的长度是一致的。

最后，我想说，线段树的题目真的难调！主要还是思路上面不是很完整，有漏洞。

#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxn = 300010;
typedef long long ll;
const ll mod = 1e9 + 9;
ll fib[maxn] = { 1, 1, 1 };
ll a[maxn];
struct node {int l, r;ll sum, f1, f2;
}tr[maxn * 4];
void pushup(node& u, node& l, node& r) {u.sum = (l.sum + r.sum) % mod;
}
void pushup(int u) {pushup(tr[u], tr[2 * u], tr[2 * u + 1]);
}
ll getFib(int n, ll a, ll b) {if (n == 1) return a % mod;if (n == 2) return b % mod;return (a % mod * fib[n - 2] % mod + b % mod * fib[n - 1] % mod) % mod;
}
ll sum(int n, ll f1, ll f2) {return ((getFib(n + 2, f1, f2) - f2) % mod + mod) % mod;
}
//void eval(int u) {
//	tr[u].sum = sum(tr[u].r - tr[u].l + 1, tr[u].f1, tr[u].f2);
//}
void pushdown(int u) {ll f1 = tr[u].f1, f2 = tr[u].f2;node& root = tr[u], & left = tr[2 * u], & right = tr[2 * u + 1];if (f1 == 0) return;left.f1 = (left.f1 + f1) % mod, left.f2 = (left.f2 + f2) % mod;right.f1 = (right.f1 + getFib(right.l - root.l + 1, f1, f2)) % mod;right.f2 = (right.f2 + getFib(right.l - root.l + 2, f1, f2)) % mod;tr[2 * u].sum += sum(left.r - left.l + 1, f1, f2);tr[2 * u].sum %= mod;ll x = getFib(right.l - root.l + 1, f1, f2);ll y = getFib(right.l - root.l + 2, f1, f2);tr[2 * u + 1].sum += sum(right.r - right.l + 1, x, y);tr[2 * u + 1].sum %= mod;tr[u].f1 = tr[u].f2 = 0;
}
void build(int u, int l, int r) {if (l == r) tr[u] = { l, r, 0, 0, 0 };else {tr[u] = { l, r, 0, 0, 0 };int mid = (l + r) / 2;build(2 * u, l, mid), build(2 * u + 1, mid + 1, r);pushup(u);}
}
void modify(int u, int l, int r) {if (l <= tr[u].l && tr[u].r <= r) {//printf("$$$ %d %d %lld %lld %lld\n", tr[u].l, tr[u].r, tr[u].f1, tr[u].f2, tr[u].sum);tr[u].f1 = (tr[u].f1 + fib[tr[u].l - l + 1]) % mod;tr[u].f2 = (tr[u].f2 + fib[tr[u].l - l + 2]) % mod;tr[u].sum += sum(tr[u].r - tr[u].l + 1, fib[tr[u].l - l + 1], fib[tr[u].l - l + 2]);tr[u].sum %= mod;//printf("### %d %d %lld %lld %lld\n", tr[u].l, tr[u].r, tr[u].f1, tr[u].f2, tr[u].sum);}else {pushdown(u);int mid = (tr[u].l + tr[u].r) / 2;if (l <= mid) modify(2 * u, l, r);if (r > mid) modify(2 * u + 1, l, r);pushup(u);}
}
node query(int u, int l, int r) {if (l <= tr[u].l && tr[u].r <= r) return tr[u];pushdown(u);int mid = (tr[u].l + tr[u].r) / 2;if (r <= mid) return query(2 * u, l, r);else if (l > mid) return query(2 * u + 1, l, r);else {node left = query(2 * u, l, r);node right = query(2 * u + 1, l, r);node res;pushup(res, left, right);return res;}
}
int main() {for (int i = 3; i < maxn; i++) fib[i] = (fib[i - 1] + fib[i - 2]) % mod;int N, M;scanf("%d%d", &N, &M);build(1, 1, N);for (int i = 1; i <= N; i++) scanf("%lld", &a[i]);for (int i = 1; i <= N; i++) a[i] = (a[i] + a[i - 1]) % mod;//printf("&$ %lld\n", a[N]);while (M--) {int t, l, r;scanf("%d%d%d", &t, &l, &r);if (t == 1) {modify(1, l, r);}else {ll ans = (((query(1, l, r).sum + a[r] - a[l - 1]) % mod) + mod) % mod;printf("%lld\n", ans);}//for (int i = 1; i <= N; i++) {//	ll ans = query(1, i, i).sum + a[i] - a[i - 1];//	printf("*** %lld %lld %lld %lld\n", ans, query(1, i, i).f1, query(1, i, i).f2, query(1, i, i).sum);//}//printf("\n");}return 0;
}

• 题意：给你一个圆，圆上有很多点，问这些点组成的三角形有多少个是包含了圆心的（圆心在三角形边上也算）。
• 思路：可以算一个点往后半个圆周内有多少个点，然后把这些点组成的三角形减掉。

#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;const int maxn = 300010;
ll a[maxn];
int N, L;
int main(){scanf("%d%d", &N, &L);for (int i = 0; i < N; i++)scanf("%lld", &a[i]);sort(a, a + N);ll ans = (ll)N * ((ll)N - 1LL) * ((ll)N - 2LL) / 6LL;for (int i = 0; i < N; i++){int u = a[i] + L / 2;ll cnt;if (u < L) {int lb = 0, ub = N;while (ub - lb > 1) {int mid = (ub + lb) / 2;if (a[mid] <= u) lb = mid;else ub = mid;}if ((a[lb] - a[i]) * 2 == L) lb--;//printf("*** %d\n", lb);cnt = lb - i;//printf("### %d\n", cnt);}else {u %= L;int lb = 0, ub = N;while (ub - lb > 1) {int mid = (ub + lb) / 2;if (a[mid] <= u) lb = mid;else ub = mid;}if ((a[i] - a[lb]) * 2 == L) lb--;//printf("*** %d\n", lb);cnt = N - (i - lb);if (u < a[0]) cnt--;}ans -= (cnt - 1) * cnt / 2;}printf("%lld\n", ans);return 0;
}
/*
4 10
0 2 3 44 10 
0 2 3 53 10
0 5 63 7
0 4 5*/