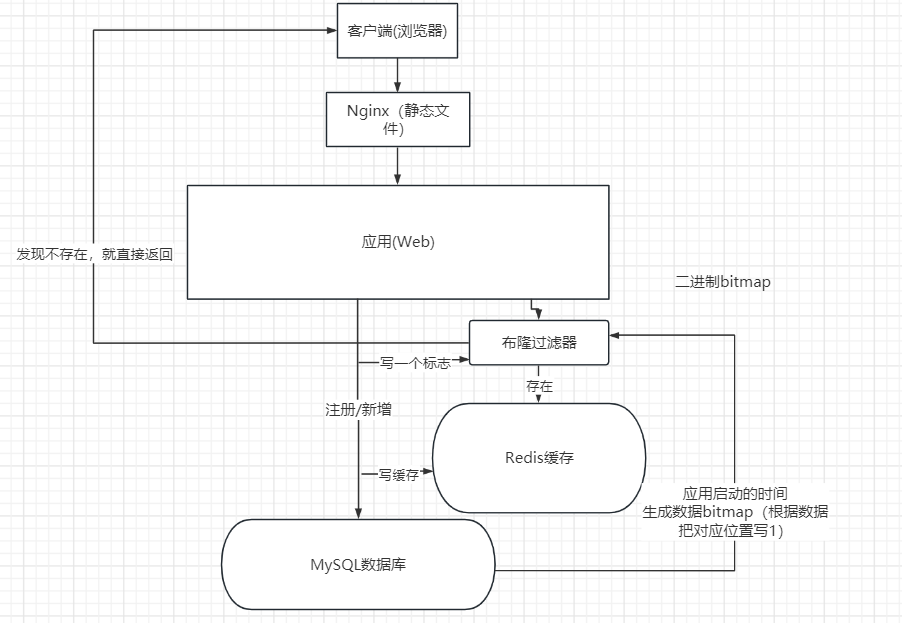
dp（3）：
1、1582F1，a[i]的值范围很小，因此我们可以暴力枚举x，使满足条件时令dp[x^a[i]]=1，那么怎么满足异或出的数列是递增的呢，我们用f[x]记录异或值为x时数列中的最大值，这样通过f数组我们就能判断是否满足条件了。
2、1552D，将a[i]=b[j]-b[k]这种关系看作一条边的话，那么对于b数组可以看作n个点n条边连成的无向图，并且这个图里必定存在一个环，也就是说存在多个a[i]的值取正或负相加等于0这个等式成立，因此我们可以用01背包解决。
3、1547E，这题用前缀最值和后缀最值处理即可。
4、1538F，可以发现对于10的增值来说，我们改变的数的数量是11，并且以此类推得出100为111，那么我们就能将数划分成各个数位计算，最后用数位dp的形式计算总值。
5、1537E1，我们贪心地取则为逐一地和s[0]比较大小，如果小于则直接判断下一个，如果相等则判断s[1]，如果大于则直接退出，以此类推得出所能取的最大位置，那么我们答案的串则为相应位置取这些位置上的相应位置即可。
需要注意的是当s[i]小于s[t]时，我们直接令pos=i+1，使得pos的值能贪心的取值而不会出现一直出现相等的情况从而使pos的值没改变。
6、1536C，当我们的比例为a:b时，那么其中能划分的所有块的比例都为a:b，如果我们暴力取的话，贪心来讲一定是从前往后取为a:b时则分为一块，显然我们这样取的块一定都能取完并比例为a:b，这样的话我们的值其实就是前i个位置中比例为a:b的数量，因此用一个map容器即可。
7、1528B，根据下面的样例解释我们可以发现，我们取dp[i]为n为i时的总数量，那么dp[i]=dp[i-1]+dp[i-2]+dp[i-3]+...+dp[1]+i的约数数量，这里求约数数量时我用求n个数的所有约数的方法时超时了，然后改用筛出所有质数及数量计算就过了。求所有约数应该是因为vector分配内存花费了大量时间所以导致超时了。
8、1528A，猜测点的值为左端点或右端点时最优的话，就是典型的树形dp，我们直接枚举点取左端点还是右端点就行了。题解证明：调整法，当我们取a[v]的值为不为端点的一个值时，令p为a[u]>a[v]的数量，q为a[u]<a[v]的数量，分析p，q的大小发现我们取端点最优。
9、1526C1，问题为典型的背包问题，但是ai的值太大，而01背包对问题的优化主要在于按体积划为同一集合，而当体积大且多时就无法实现优化，可以发现n的值比较小，所以我们可以换一种状态表示即dp[i][j]表示取到i这个位置且已经取了j个数的价值的最大值，分析转移即可。
10、1517D，直接暴力，用dp[i][j][k]表示i，j这个位置上走k步的最小代价，可以发现我们走的路线一定是一条的，即去和回是同样的路线，所以当k为偶数时才有值，并且为dp[i][j][k/2]的两倍。