OJ刷题第十五篇（递推较多，奥赛篇）

31005 - 昆虫繁殖（难度非常大，信息奥赛题）

时间限制 : 1 秒

内存限制 : 128 MB

科学家在热带森林中发现了一种特殊的昆虫，这种昆虫的繁殖能力很强。每对成虫过x个月产y对卵，每对卵要过两个月长成成虫。假设每个成虫不死，第一个月只有一对成虫，且卵长成成虫后的第一个月不产卵(过x个月产卵)，问过z个月以后，共有成虫多少对？0≤x≤20,1≤y≤20,X≤z≤50。

输入

x,y,z的数值。

输出

过z个月以后，共有成虫对数。

样例

输入

1 2 8

输出

答案：

#include<iostream>
using namespace std;
int main()
{long long c[52] = { 0 }, r[52] = { 0 };//c[i]表示第i月成虫总数量，以对为单位，r[i]表示第i月新产生虫卵数量int x, y, z;cin >> x >> y >> z;for (int i = 1; i <= x; i++) {//前x个月没有产卵，因此这几个月成虫数量为1对，虫卵数量为0c[i] = 1;r[i] = 0;}//求Z月之后，成虫数量for (int i = x+1; i <= z + 1; i++) {r[i] = c[i - x] * y;c[i] = c[i - 1] + r[i - 2];  }cout << c[z + 1] << endl;return 0;
}

分析：本题难度非常大，首先是对题目的理解，整理如下：

1、每过x个月产一对卵，如果从第一个月开始算，假设我们只算第一对的产卵数量，假设x为1，则在第2月开始产卵，第三月也要产卵，以此类推；如果x为2，则从第三月开始产卵，第5月又要产卵，以此类推。因此每过x月产卵，即在当前月份+x得到的月份数即要开始产卵了。

2、题目求的是z月之后，比如z为8，即过了8个月之后，则隐含告诉我们就是求第9月的成虫数量。这是本题一个难点。

3、本题的核心是找出递推关系。设两个数组c[i]表示第i个月的成虫数量，r[i]表示第i个月的新产的虫卵数量，注意为什么强调是第i个月新产的虫卵数量。看下面推到：

先求c[i]：

我先告诉你结论，c[i]=c[i-1]+r[i-2]，即第i月的成虫数量等于上一个月的成虫数量加上前两个月新产生的虫卵数量，就得到第i月的成虫数量。因为题目明确说了过了两个月虫卵才可以长成成虫。（这里题目可以加大难度，可以设一个变量，比如m月，那么原推倒就是c[i]=c[i-1]+r[i-m]）

再求r[i]：

注意，第i月的成虫数量只跟某个月新产生的虫卵数量有关，先告诉结论：r[i]=c[i-x]*y，因为题目说的是每过x个月才开始产卵，因此我们求第i月的卵虫数量要在前面第i-x月的成虫数量中去找，比如x=1,y=2,假设当前是第5月，求第5月新产生的虫卵数量，我们要在第5-1=4,第4月中去找，因为它是每过x=1个月开始产卵，不知道你理解没有。仔细理解。比如x=2,y=2，当前仍然是第5月，求第5月新产生的虫卵，我们要在5-2=3，第三月的成虫数量中去找，r[5]=c[5-2]*2，即第3月的成虫数量乘以y(y这里为2)，就得到第5月的新虫卵的数量。这里很难理解。也是本题最难的地方。因为虫卵是由成虫产生的，而我们现在求的是每月新产生的虫卵数量，新产生的虫卵只跟第i-x月的成虫数量有关，第i-x月的成虫产卵，过了x月，就得到第i月的新产生的虫卵数量。

是否通过：

31006 - 位数问题（难题，信息奥赛题，二刷、三刷、甚至四刷！）

时间限制 : 1 秒

内存限制 : 128 MB

在所有的N位数中，有多少个数中有偶数个数字3?由于结果可能很大，你只需要输出这个答案对12345取余的值。

输入

读入一个数N(N≤1000)。

输出

输出有多少个数中有偶数个数字3。

样例

输入

输出

#include<iostream>
using namespace std;
int main() {int a[1001], b[1001];//a[i]表示i位数中偶数3的个数，b[i]表示i位数中奇数3的个数int N;cin >> N;a[1] = 9;b[1] = 1;int x = 9;for (int i = 2; i <= N; i++) {if (i == N) {x = x - 1;}a[i] = (x * a[i - 1] + 1 * b[i - 1]) % 12345;b[i] = (x * b[i - 1] + 1 * a[i - 1]) % 12345;}cout << a[N] << endl;return 0;
}

分析：这个题难度非常大，首先对题目的意思可能就有很多人没理清。或者很多人一开始就是一个一个数的判断，这样对小规模的数可以，但是N大到一定数以后，就会运行超时。我当时在做的时候反正是没想到这是个递推。。看来是题目见得少。再开始分析之前有一点我们有必要知道：

偶数=偶数+偶数或者偶数=奇数+奇数

奇数=奇数+偶数或者奇数=偶数+奇数

下面开始分析：

当N=1时，即从0到9这10个数中，偶数个3的个数，很多人以为是0，因为只有一个3，没有偶数个，你别忘了，0它也是偶数，因此0~2 ，4~9都是0个3，即偶数个3有9个，奇数个3有1个。

当N为2时，即从10~99，我们最高位即十位不能为0，只能取1~9,。分两种情况：

当十位为偶数位3时时，即十位取1~2或者4~9，共8种情况，要想使得整个数3的个数为偶数，则个位上3的个数也必须为偶数个，而个位上可以取0，即,0~2,4~9，即9种情况。共有8*9=72种；

当十位为奇数个3时，即30~39，要想使得整个数3的个数为偶数个，那么个位数上的3的个数只能取奇数个，只有一种情况，即33。

故共有72+1=73种。

当N为3时，即从100~999，分析是一样的道理：

当百位为偶数个3，即1~2,4~9共8种情况，这时候只需让后面的十位和个位都取偶数位即可，且只能取偶数个3。注意，现在十位和个位都不是最高位，因此都能取到0，即0~2,4~9共9种，因此共有8*9*9=648种。

还有一种就是百位为偶数位，后面的十位和个位均为奇数位。即有

8*1*1=8种。

当百位为奇数位时，即只能取3，后面的十位和个位加起来得是奇数。若十位为偶数位，即~2,4~9，则个位只能取奇数个3，即个位只能取3，有1*9*1=9种；若十位为奇数位，即十位只能取3，则个位只能取偶数位，共1*1*9=9种。

共648+8+18=674种。

好了，到这里，我想你应该看出有那种递推的思想了。我们两个数组，a[i]、b[i]分别表示i为数的偶数个3的个数和奇数个3的个数。可以得到如下递推式子：

a[i] = x * a[i - 1] + 1 * b[i - 1];（偶数等于偶数加偶数或者奇数加奇数）
b[i] = x * b[i - 1] + 1 * a[i - 1];（奇数等于奇数加偶数或者偶数加奇数）

其中x=9。

a[i] = x * a[i - 1] + 1 * b[i - 1];它的意思是在i为数中，求偶数个3的个数等于两种情况

1、第一位为偶数个3时，共x*a[i-1]

2、第一位为奇数个3时，共1*b[i-1]

b[i] = x * b[i - 1] + 1 * a[i - 1];它的意思是在i位数中，求奇数个3的个数等于两种情况：

1、第一位为奇数个，共有1 *a[i-1]

2、第一位为偶数个，共有x*b[i-1]

共b[i] = x * b[i - 1] + 1 * a[i - 1]个

这个递推式是很难推出来的，而且这个版本比其他博主写的更难，因为把奇数的那一部分也求出来了。不仅能求偶数个，也能求奇数个。

但是这里要注意一点是，当求到最高位时，由于最高位不能取0，因此x得减1。

是否通过：

31007 - 过河卒（经典问题！也是难题！）

时间限制 : 1 秒

内存限制 : 128 MB

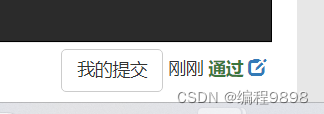
棋盘上A点有一个过河卒，需要走到目标B点。卒行走的规则：可以向下、或者向右。同时在棋盘上的某一点有一个对方的马（如C点），该马所在的点和所有跳跃一步可达的点称为对方马的控制点，如图中的C点和P1，……，P8，卒不能通过对方马的控制点。棋盘用坐标表示，A点(0,0)、B点(n, m) (n,m为不超过20的整数),同样马的位置坐标是需要给出的，C≠A且C≠B。现在要求你计算出卒从A点能够到达B点的路径的条数。

输入

给出n、m和C点的坐标。

输出

从A点能够到达B点的路径的条数。

样例

输入

8 6 0 4

输出

答案：

#include<iostream>
using namespace std;
long long dp[100][100];//因为第一次设置为int型，数据发生溢出，因此设置为long long类型
int main() {int n, m, x, y;cin >> n >> m >> x >> y;for (int i = 0; i <= n; i++) {for (int j = 0; j <= m; j++) {//先把每个点初始化为1，表示到该该点路径数为1dp[i][j] = 1;}}//对马的点和马的控制点进行赋值，使到这些点的路径数为0dp[x][y] = 0;if (x + 2 >= 0 && y + 1 >= 0)dp[x + 2][y + 1] = 0;if (x + 1 >= 0 && y + 2 >= 0)dp[x + 1][y + 2] = 0;if (x - 1 >= 0 && y + 2 >= 0)dp[x - 1][y + 2] = 0;if (x - 2 >= 0 && y + 1 >= 0)dp[x - 2][y + 1] = 0;if (x - 2 >= 0 && y - 1 >= 0)dp[x - 2][y - 1] = 0;if (x - 1 >= 0 && y - 2 >= 0)dp[x - 1][y - 2] = 0;if (x + 1 >= 0 && y - 2 >= 0)dp[x + 1][y - 2] = 0;if (x + 2 >= 0 && y - 1 >= 0)dp[x + 2][y - 1] = 0;//计算每个点的路径数for (int i = 0; i <= n; i++) {for (int j = 0; j <= m; j++) {if (i == 0 && j == 0) {//出发点不做任何处理continue;}if (dp[i][j] == 0) {//遇到马点和马的控制点也不不做任何处理continue;}//由于点的移动只能向右或者向下，对第一行和第一列要单独处理if (i == 0) {//第一行，若第一行有马点或马的控制点，则后面的点都不可达，设置为前一个点的值dp[i][j] = dp[i][j - 1];}if (j == 0) {//第一列，若第一列有马点或者马的控制点，则下面的点都不可达，设置为前一个点的值dp[i][j] = dp[i - 1][j];}if (i != 0 && j != 0) {//除了第一行、第一列以及马点和马的控制点，处理剩下的点dp[i][j] = dp[i][j - 1] + dp[i - 1][j];}}}cout << dp[n][m] << endl;return 0;
}

分析：在做这个题之前，我是没什么头绪的，是查阅了资料进行整理才解决这个题。这个题是移动路线题的升级版。什么是移动路线，在力扣刷题库里，第64题。搞懂这个题，这个过河卒理解起来就简单多了。这个题难点就在处理马点和马的控制点。

首先我们要知道8个控制点怎么表示，其次得判断它们的合法性

其次就是对一一行和第一列的处理，这是许多这种类似题都要处理的地方。因为第一列和第一行比较特殊。所以要单独处理。

是否通过：

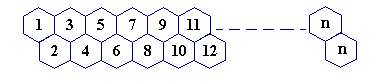
31008 - 蜜蜂路线（难题！高进度加法！！）

时间限制 : 1 秒

内存限制 : 128 MB

一只蜜蜂在下图所示的数字蜂房上爬动,已知它只能从标号小的蜂房爬到标号大的相邻蜂房,现在问你：蜜蜂从蜂房 M 开始爬到蜂房 N，M<N，有多少种爬行路线？（备注：题面有误，右上角应为 n-1）

输入

输入 M，N 的值。

输出

爬行有多少种路线。

样例

输入

1 14

输出

提示

对于100%的数据，M,N <= 1000

答案：

#include<iostream>
using namespace std;
int n, m, a[5005] = { 1 }, b[5005] = { 1 }, c[5005] = { 1 }, len = 1;
void f() {int jw = 0;for (int i = 0; i < len; i++) {c[i] = a[i] + b[i] + jw;jw = c[i] / 10;c[i] %= 10;}if (jw != 0) {c[len] = jw;len++;}for (int i = 0; i < len; i++) {a[i] = b[i];b[i] = c[i];}
}
int main() {cin >> m >> n;for (int i = 3; i <= n - m + 1; i++) {f();}for (int i = len - 1; i >= 0; i--) {cout << c[i];}return 0;
}

分析：其实这道题逻辑很简单，就是一个题目变换的斐波那契数列，推倒公式为

f(n)=f(n-1)+f(n-2)，但是我们知道，之前做的斐波那契数列在第46项就已经达到18亿，第47项溢出，即使改为long long类型，也只是到第103项，题目给出N最大可以到1000项，显然long long类型也是不够的。那么怎么办呢？用double吗？？你要知道，斐波那契数列是指数级增长的，平时的加法已经在这里不适用了。因为后面的数都太大了，所以这个题要用到高精度加法，也就是我们熟悉的大数加法运算。所以很多人在这个题用long long只能通过前两个测试点，第三个测试点不能通过。

大数加法怎么做呢？很简单就是模拟普通加法运算，我们需要借助一个变量作为进位，设进位变量为jw，初始值为0。

每当一个数进行加以后，我们取的是后面那一位的值，比如8+6=14，这一位取4,1向前面进位。

设a[i]和b[i]分别表示两个大数，c[i]表示两数求的和，两数相加时有如下：

c[i]=a[i]+b[i]+jw;

jw=c[i]/10;

c[i]=c[i]%10;

这是大数加法运算得核心步骤。然后再用一个全局变量记录 c[i]即和的长度，然后把

a[i]=b[i];

b[i]=c[i];

这个是实现递推。到这里说一下我的感受，OJ系统到这里都是一些比较难的题目了，而且难度明显比之前难了不少。但是之前那些题可能见得比较多，所以上手起来并不是很难，而后面这些题遇到的不多，尤其像这个大数加法，遇到的是真的不多，因此后面二刷甚至三刷的时候建议多刷这种题，这也是比赛喜欢出的题。

是否通过：

31011 - 上台阶

时间限制 : 1 秒

内存限制 : 128 MB

楼梯有n(71>n>0)阶台阶,上楼时可以一步上1阶,也可以一步上2阶,也可以一步上3阶，编程计算共有多少种不同的走法。

输入

输入的每一行包括一组测试数据，即为台阶数n。最后一行为0，表示测试结束。

输出

每一行输出对应一行输入的结果，即为走法的数目。

样例

输入

输出

答案：

#include<iostream>
using namespace std;
int main() {int n;while (true) {cin >> n;if (n) {long long sum = 0,f1=1,f2=2,f3=4;if (n == 1) {sum = f1;}else if (n == 2) {sum = f2;}else if (n == 3) {sum = f3;}else {for (int i = 4; i <= n; i++) {sum = f1 + f2 + f3;f1 = f2; f2 = f3;f3 = sum;}}cout << sum << endl;}else {break;}}return 0;
}

分析：这道题其实之前做了，骨牌铺法那道题就是三层推导，或者说是三个递推关系f(n)=f(n-1)+f(n-2)+f(n-3)，这里写在这里就是回顾一下，另外要知道f3=4为什么？？

假设第一步：有三种走法，第一个阶梯，第二个阶梯，第三个阶梯，走到第二和第三其实这只能是一种走法，走到第三阶梯后面没阶梯了，因此这是一种，其次走到第二阶梯，剩下一个阶梯也只能有一种走法。

如果第一步走到第一个阶梯，那么剩下的两种阶梯就有两种走法，要么一步一步走到第三阶梯，要么一步走到第三阶梯，因此共4种走法。