文章目录
- 1.QQ图原理:
- 2.效果图:
- 3.代码:
1.QQ图原理:
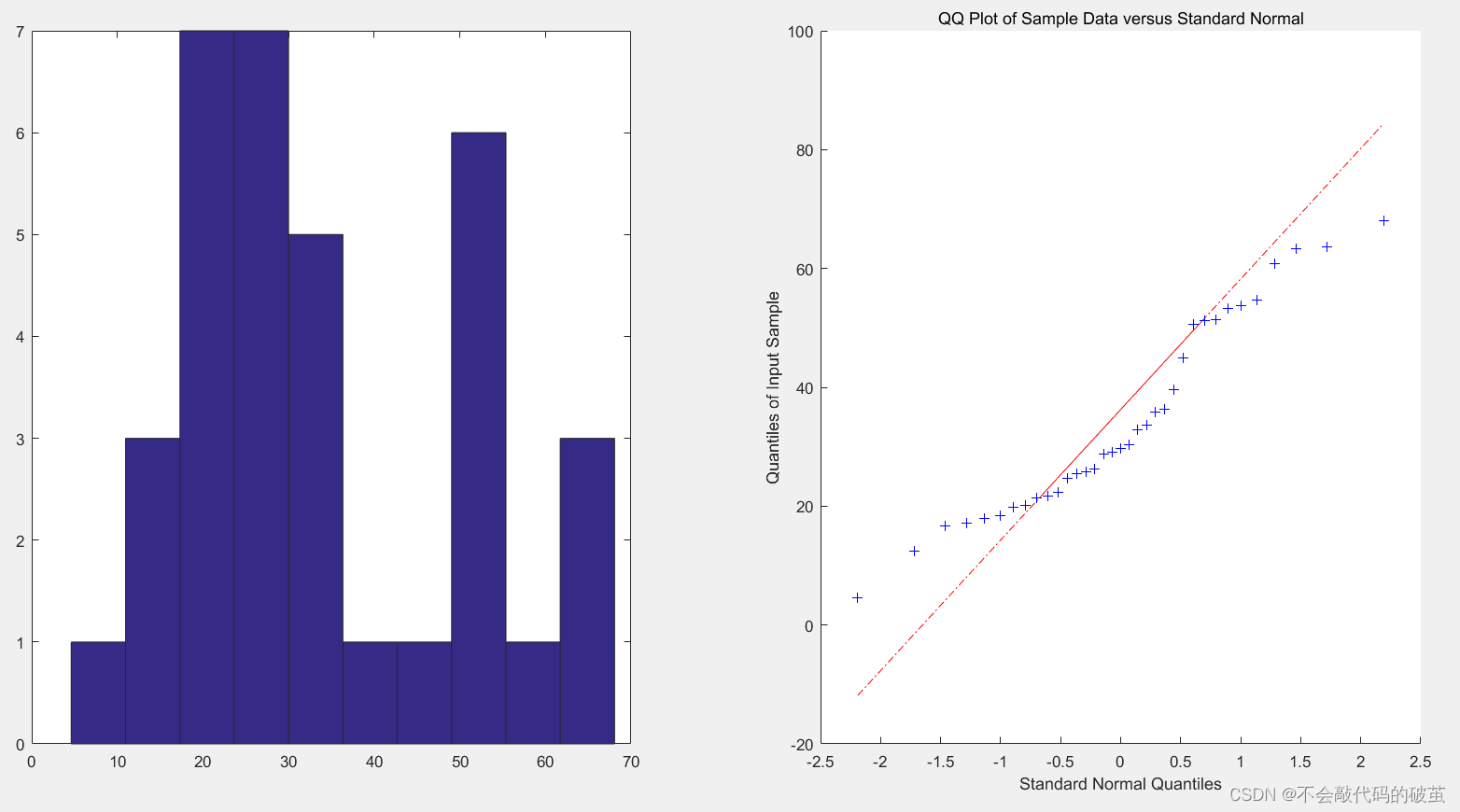
数据中一串数目的每个点都是该数据的某分位点,把这些点的(称为样本分位数点)和相应的理论上的分位数配对做出散点图,如果该数据服从正态分布,那么该图看上去应该像一条直线,否则就不服从正态分布。
2.效果图:
3.代码:
function test7()
data=[36.28
20.14
4.61
33.59
29.64
53.79
50.61
19.79
68.08
63.3
35.78
39.57
32.93
26.25
16.71
18.46
51.26
51.33
12.41
21.7
60.74
53.33
28.79
54.61
17.98
45.02
24.61
21.35
25.74
63.66
22.28
17.11
29.15
25.42
30.39
];
%x是要检验的数据
figure(1)
subplot(1,2,1)
hist(data) %直方图上看,ph是偏右的,并非正太分布
subplot(1,2,2)
qqplot(data) %QQ图上看,ph的分位数跟标准正态分布的分位数并非线性,印证了ph不接近正态分布