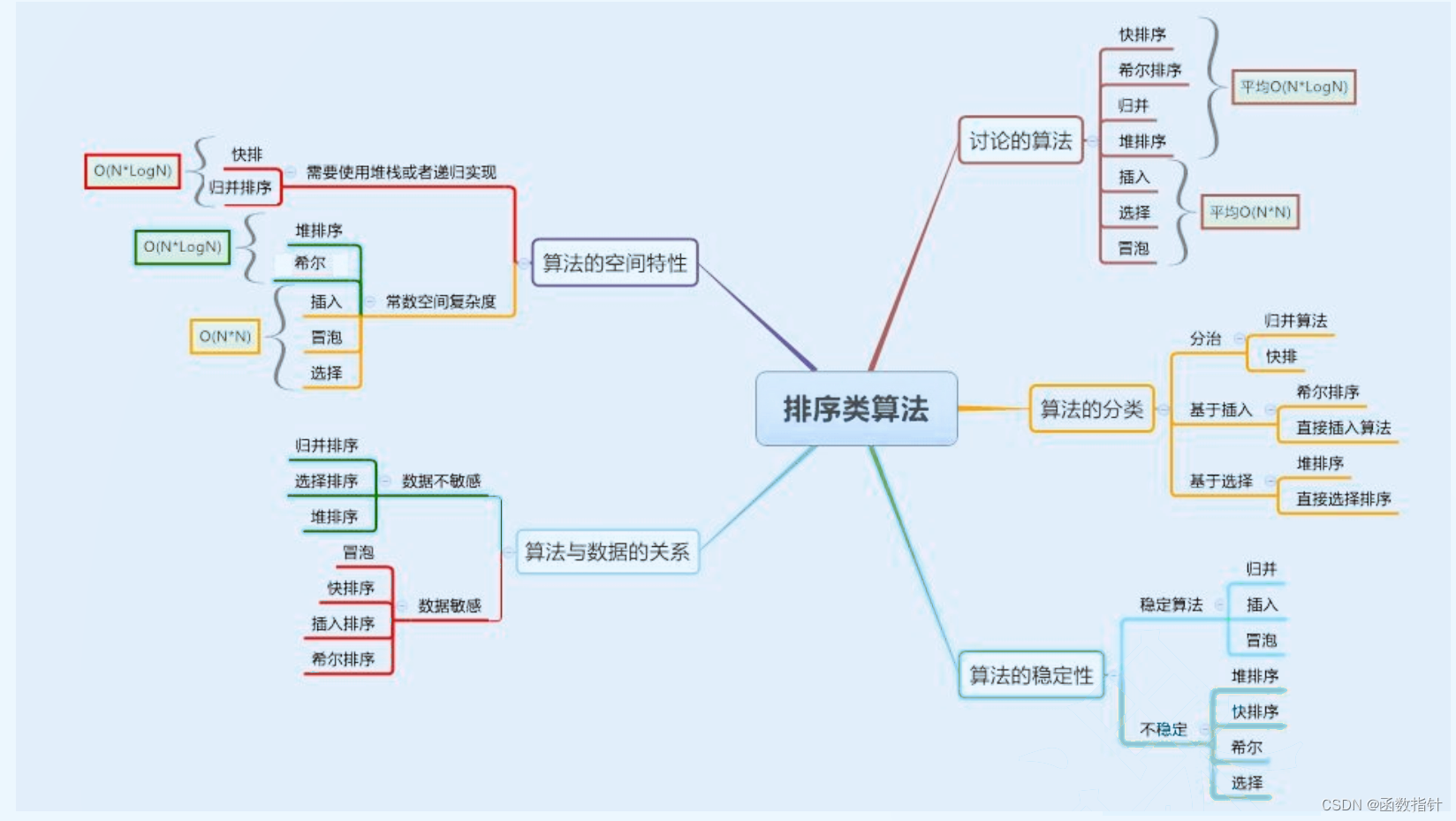
归并排序：是创建在归并操作上的一种有效的排序算法。算法是采用分治法（Divide and Conquer）的一个非常典型的应用，且各层分治递归可以同时进行。归并排序思路简单，速度仅次于快速排序，为稳定排序算法，一般用于对总体无序，但是各子项相对有序的数列。

1. 基本思想

归并排序是用分治思想，分治模式在每一层递归上有三个步骤：

• 分解（Divide）：将n个元素分成个含n/2个元素的子序列。
• 解决（Conquer）：用合并排序法对两个子序列递归的排序。
• 合并（Combine）：合并两个已排序的子序列已得到排序结果。

归并排序的特性总结：

1. 归并的缺点在于需要O(N)的空间复杂度，归并排序的思考更多的是解决在磁盘中的外排序题。
2. 时间复杂度：O(N*logN)
3. 空间复杂度：O(N)
4. 稳定性：稳定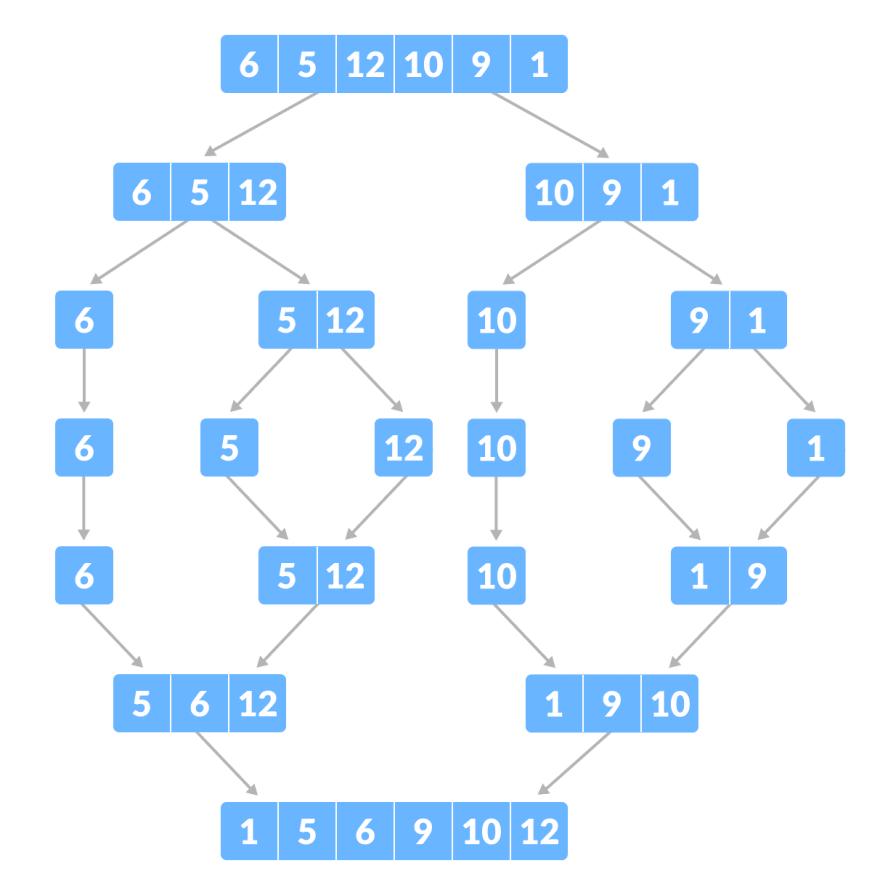

 这是归并排序的主要概念。

归并排序有递归和非递归两种，我们首先来实现递归的代码

代码

//归并递归
void _MergeSore(int* arr, int left, int right, int* tmp)
{//递归结束条件if (left >= right)return;//int min = left + ((right - left) >> 1);int min = (left + right) / 2;//递归开始_MergeSore(arr, left, min, tmp);_MergeSore(arr, min + 1, right, tmp);//排序开始int begin1 = left, end1 = min;int begin2 = min + 1, end2 = right;int i = left;while (begin1 <= end1 && begin2 <= end2){if (arr[begin1] < arr[begin2]){tmp[i++] = arr[begin1++];/*i++;begin1++;*/}if (arr[begin1] >= arr[begin2]){tmp[i++] = arr[begin2++];/*i++;begin2++;*/}}while (begin1 <= end1){tmp[i++] = arr[begin1++];}while (begin2 <= end2){tmp[i++] = arr[begin2++];}//将建立的数组拷贝到原数组中for (int i = 0; i <= right; i++){arr[i] = tmp[i];}
}
//归并排序
void MergeSort(int* arr, int n)
{//先建立一个数组，用来存放排序的元素int* tmp = (int*)malloc(sizeof(int) * (n));if (tmp == NULL){perror("perror,file");return;}//归并函数实现_MergeSore(arr, 0, n - 1, tmp);//销毁新建数组，防止内存泄漏free(tmp);//防止野指针tmp = NULL;
}

下面是非递归的写法，非递归的思想与递归的思想几乎一样，大家可以自己想下过程。

1.  申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列
2.  设定两个指针，最初位置分别为两个已经排序序列的起始位置
3.  比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置
4.  重复步骤③直到某一指针到达序列尾
5.  将另一序列剩下的所有元素直接复制到合并序列尾

void _MergeSoreNonR1(int* arr, int left, int right, int* tmp)
{int gap = 1;int i = 0;while (gap <= right){for (i = 0; i <= right; i += 2 * gap){//[i,I+gap-1]  [i+gap,2*gap-1]int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;//printf(" %d", end2);if (end1 > right)end1 = right;if (begin2 > right){begin2 = right + 1;end2 = right;}if (end2 > right)end2 = right;int index = i;while (begin1 <= end1 && begin2 <= end2){if (arr[begin1] < arr[begin2]){tmp[index++] = arr[begin1++];}if (arr[begin1] >= arr[begin2]){tmp[index++] = arr[begin2++];}}while (begin1 <= end1){tmp[index++] = arr[begin1++];}while (begin2 <= end2){tmp[index++] = arr[begin2++];}}for (i = 0; i <= right; i++){arr[i] = tmp[i];}gap *= 2;}
}void MergeSortNonR(int* arr, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc,file");return;}_MergeSoreNonR1(arr, 0, n-1, tmp);free(tmp);tmp = NULL;
}

下面来看计数排序

计数排序不用比较两个数的大小，它的做法是统计哪个元素出现的次数，然后通过这个元素出现的次数来排序。

计数算法只能使用在已知序列中的元素在0-k之间，且要求排序的复杂度在线性效率上。 Â 计数排序和基数排序很类似，都是非比较型排序算法。但是，它们的核心思想是不同的，基数排序主要是按照进制位对整数进行依次排序，而计数排序主要侧重于对有限范围内对象的统计。基数排序可以采用计数排序来实现。

计数排序的特性总结：
1. 计数排序在数据范围集中时，效率很高，但是适用范围及场景有限。
2. 时间复杂度：O(MAX(N,范围))
3. 空间复杂度：O(范围)
4. 稳定性：稳定

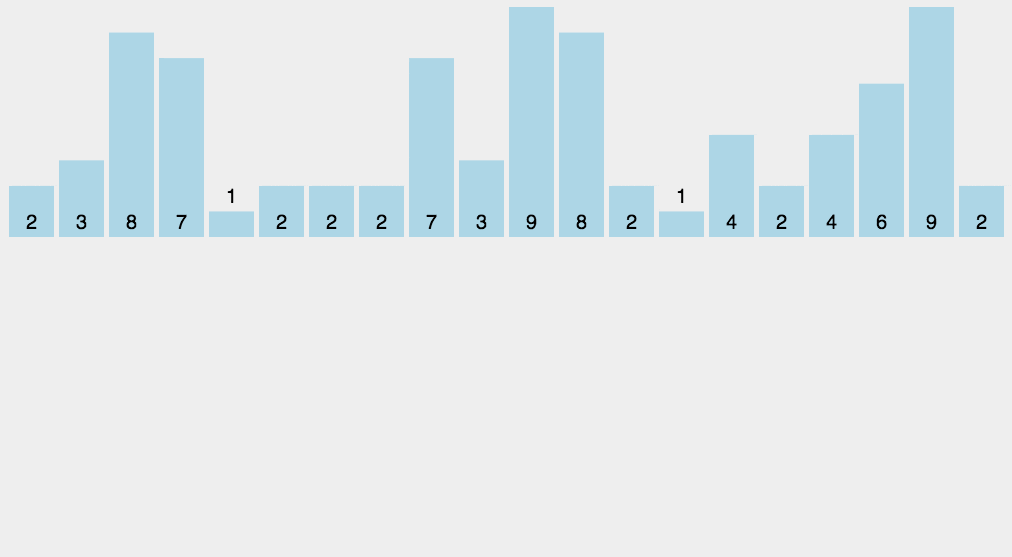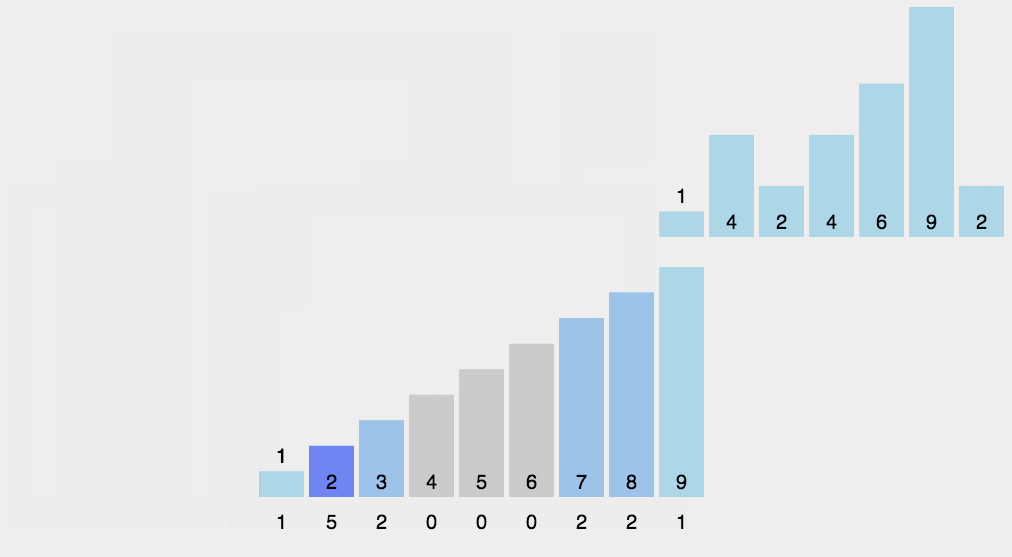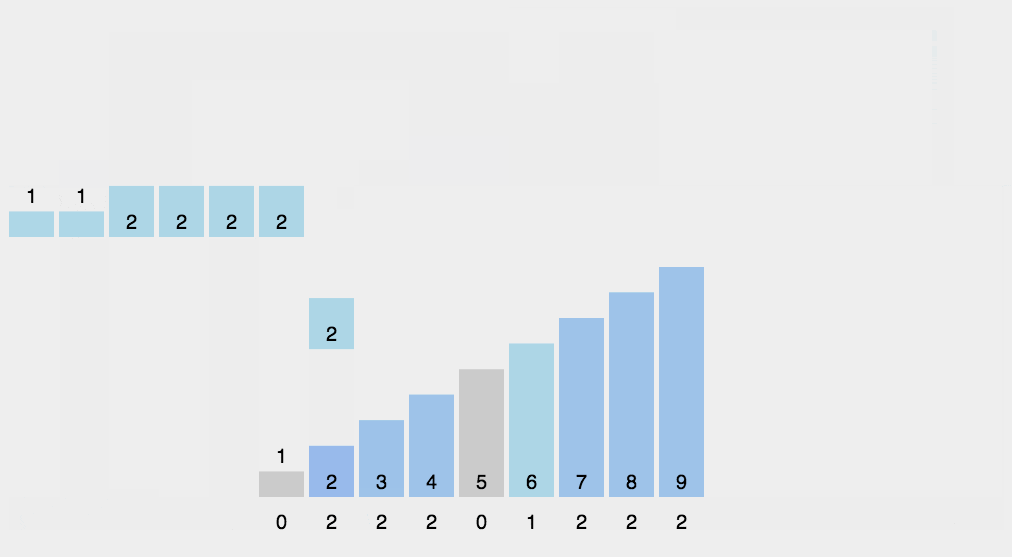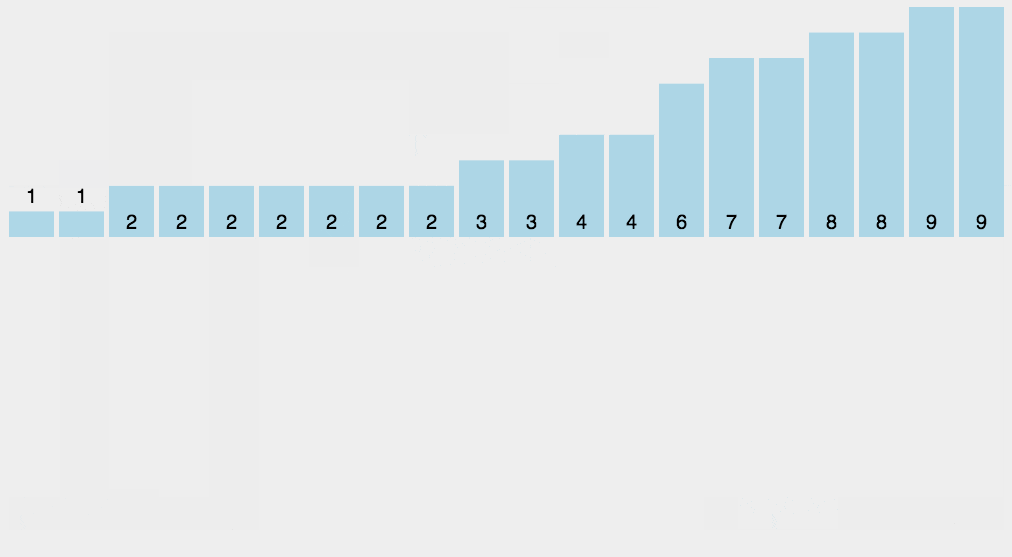
代码实现

void CountSort(int* arr, int n)
{//确定数组开辟的大小int max = arr[0], min = arr[0];for (int i = 1; i < n; i++){if (arr[i] > max)max = arr[i];if (arr[i] < min)min = arr[i];}int range = max - min + 1;//建立一个数组int* count = (int*)malloc(sizeof(int) * range);if (count == NULL){perror("malloc file");return NULL;}memset(count, 0, sizeof(int) * range);for (int i = 0; i < n; i++){count[arr[i]-min]++;}int j = 0;for (int i = 0; i < n; i++){while (count[i]--){arr[j] = i+min;j++;}}free(count);count = NULL;
}

 下面是一张八大排序的比较图