A. A-characteristic

题目链接：

Problem - A - Codeforces

题面：

题意：

有一个数组a，里面只存在1和-1，现在可以选择任意两个位置，但是不能重合，如果两个位置的数乘积为1，那么特点数累加，题目给定一个n和k，要求构造一个长度为n的数组，使特点数为k

思路：

一个数组如果有两个1，那么特点数为1；如果有三个1，那么特点数为3，如果有4个1，那么特点数为6；-1也是如此，那么我们可以枚举1的数量，如果1提供的特点数和-1的提供特点数之和为k，那么就是可以构造，同时我们也知道了1和-1的数量

代码：

#include<bits/stdc++.h>
using namespace std;int arr[105];int main(){int t;cin >> t;while(t--){int n, m;cin >> n >> m;int a = 1;arr[1] = 0;arr[0] = 0;for(int i = 2; i <= n; i++){arr[i] = arr[i - 1] + a;a++;}bool f = 0;a = 0;int b = 0;for(int i = 1; i <= n; i++){if(arr[i] + arr[n - i] == m){f = 1;a = i, b = n - i;break;}}if(f){cout << "YES" << endl;f = 0;for(int i = 0; i < a; i++){if(f){cout << " ";}f = 1;cout << 1;}for(int i = 0; i < b; i++){if(f){cout << " ";}f = 1;cout << -1;}cout << endl;}else{cout << "NO" << endl;}}return 0;
} 

B. Sort with Step

题目链接：

Problem - B - Codeforces

题面：

题意：

有一个长度为n的数组p，p中的数为1-n且每个只会出现1次。你可以对数组进行无数次的操作：

选择两个位置i，j；如果abs（i-j） == k，那么就可以交换两个位置的值。

你也可以对数组进行一次特殊操作：

任选两个位置交换

先给定n，k和一个长度为n的数组，要求给这个数组排成一个递增的数组，

如果不需要进行特殊操作就输出0，

如果需要进行一次特殊操作就输出1，

如果需要不止一次就输出-1

思路：

因为这个数组每个位置的值是1-n且只会出现一次，那么最后排序结果为

a1 = 1，a2 = 2 .... an = n

那么我们记录每个值的位置，以及通过判断差值的绝对值和k的关系就可以知道是否需要特殊操作以及特殊操作的次数

如果差值的绝对值都是是k的倍数，那么就不需要特殊操作。如果有两个不是，那么就需要一次特殊操作，如果超过两个，那么就需要多次特殊操作

代码：

#include<bits/stdc++.h>
using namespace std;int arr[200005], num[200005];int main(){int t;cin >> t;while(t--){int n, m;cin >> n >> m;int a;for(int i = 1; i <= n; i++){cin >> a;arr[a] = abs(a - i);}int ans = 0;for(int i = 1; i <= n; i++){if(arr[i] % m == 0){num[i] = 1;}else{ans++;num[i] = -1;}}if(ans == 0){cout << 0 << endl;}else if(ans == 2){cout << 1 << endl;}else{cout << -1 << endl;}}return 0;
} 

C. Strongly Composite

题目链接：

Problem - C - Codeforces

题面：

 

题意：

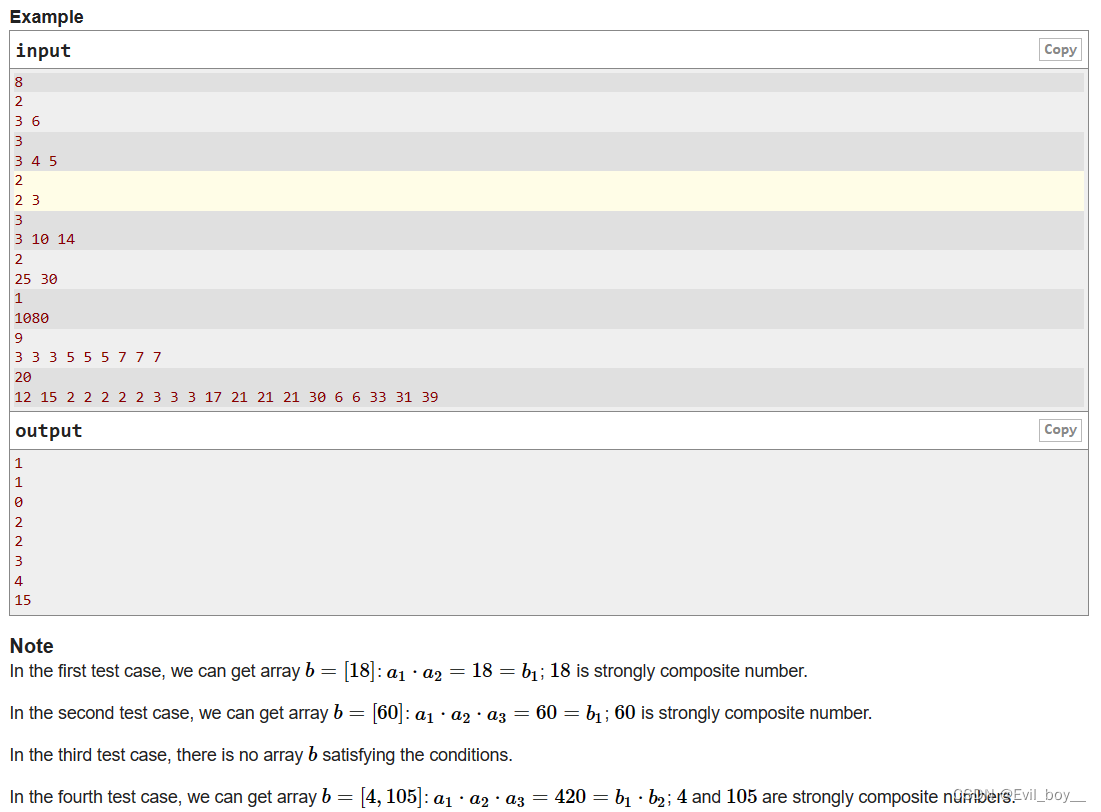
一个数如果它的质因子的数量小于等于它的非质因子（1除外）的数量，那么这个数是强合性的，

现在给定n个数，问最多能找出几个强合性的数，使乘积相同

思路：

如果一个数有两个相同的质因子，那么这个数就是强合性的，如4，9.如果一个数只有两个不同的质因子，那么就不是，如6，如果有3个质因子，那么就会是，如30.

那么我可以统计出这n个数的所有质因子的数量，因为我们要使强合性的数的数量尽可能的多，那么相同的质因子两两合并，不同的三个合并即可

代码：

#include<bits/stdc++.h>
using namespace std;int arr[200005], num[200005];int main(){int t;cin >> t;while(t--){int n, m;cin >> n >> m;int a;for(int i = 1; i <= n; i++){cin >> a;arr[a] = abs(a - i);}int ans = 0;for(int i = 1; i <= n; i++){if(arr[i] % m == 0){num[i] = 1;}else{ans++;num[i] = -1;}}if(ans == 0){cout << 0 << endl;}else if(ans == 2){cout << 1 << endl;}else{cout << -1 << endl;}}return 0;
}