pcl中features模块又基于惯性矩和偏心率的描述子,也可以求取点云的AABB和OBB包围盒,在计算的过程中法线一些问题,特此记录。
针对惯性矩和偏心率这两个数据的应用场景还不明确,因此暂时不做讨论,主要讨论求取OBB时的代码。
template <typename PointT> void
pcl::MomentOfInertiaEstimation<PointT>::computeOBB ()
{obb_min_point_.x = std::numeric_limits <float>::max ();obb_min_point_.y = std::numeric_limits <float>::max ();obb_min_point_.z = std::numeric_limits <float>::max ();obb_max_point_.x = std::numeric_limits <float>::min ();obb_max_point_.y = std::numeric_limits <float>::min ();obb_max_point_.z = std::numeric_limits <float>::min ();unsigned int number_of_points = static_cast <unsigned int> (indices_->size ());for (unsigned int i_point = 0; i_point < number_of_points; i_point++){float x = (input_->points[(*indices_)[i_point]].x - mean_value_ (0)) * major_axis_ (0) +(input_->points[(*indices_)[i_point]].y - mean_value_ (1)) * major_axis_ (1) +(input_->points[(*indices_)[i_point]].z - mean_value_ (2)) * major_axis_ (2);float y = (input_->points[(*indices_)[i_point]].x - mean_value_ (0)) * middle_axis_ (0) +(input_->points[(*indices_)[i_point]].y - mean_value_ (1)) * middle_axis_ (1) +(input_->points[(*indices_)[i_point]].z - mean_value_ (2)) * middle_axis_ (2);float z = (input_->points[(*indices_)[i_point]].x - mean_value_ (0)) * minor_axis_ (0) +(input_->points[(*indices_)[i_point]].y - mean_value_ (1)) * minor_axis_ (1) +(input_->points[(*indices_)[i_point]].z - mean_value_ (2)) * minor_axis_ (2);if (x <= obb_min_point_.x) obb_min_point_.x = x;if (y <= obb_min_point_.y) obb_min_point_.y = y;if (z <= obb_min_point_.z) obb_min_point_.z = z;if (x >= obb_max_point_.x) obb_max_point_.x = x;if (y >= obb_max_point_.y) obb_max_point_.y = y;if (z >= obb_max_point_.z) obb_max_point_.z = z;}obb_rotational_matrix_ << major_axis_ (0), middle_axis_ (0), minor_axis_ (0),major_axis_ (1), middle_axis_ (1), minor_axis_ (1),major_axis_ (2), middle_axis_ (2), minor_axis_ (2);Eigen::Vector3f shift ((obb_max_point_.x + obb_min_point_.x) / 2.0f,(obb_max_point_.y + obb_min_point_.y) / 2.0f,(obb_max_point_.z + obb_min_point_.z) / 2.0f);obb_min_point_.x -= shift (0);obb_min_point_.y -= shift (1);obb_min_point_.z -= shift (2);obb_max_point_.x -= shift (0);obb_max_point_.y -= shift (1);obb_max_point_.z -= shift (2);obb_position_ = mean_value_ + obb_rotational_matrix_ * shift;
}
如上所示,OBB求取的过程就是将点云转换到以中心为坐标原点,PCA计算的三个特征向量为轴方向的局部坐标系中,然后求取相应的AABB包围盒的过程,但是在文中最后一段
Eigen::Vector3f shift ((obb_max_point_.x + obb_min_point_.x) / 2.0f,(obb_max_point_.y + obb_min_point_.y) / 2.0f,(obb_max_point_.z + obb_min_point_.z) / 2.0f);obb_min_point_.x -= shift (0);obb_min_point_.y -= shift (1);obb_min_point_.z -= shift (2);obb_max_point_.x -= shift (0);obb_max_point_.y -= shift (1);obb_max_point_.z -= shift (2);obb_position_ = mean_value_ + obb_rotational_matrix_ * shift;
第一点:
shift是包围盒的在局部坐标系中的中心坐标,
obb_rotational_matrix_ 是将局部坐标系转为全局坐标的旋转矩阵,平移矩阵就是中心点坐标。
obb_position_ 就是OBB包围盒中心的全局坐标
注意:这里局部坐标系和全局坐标系的转换关系要注意,对点云计算协方差阵,得到的特征向量矩阵是列向量组成的,obb_rotational_matrix_ 就是列向量组成的;
分析:
全局坐标->局部坐标
RP=Pt,此时的R是特征向量作为行向量组成的,这与得到的特征向量矩阵是转置的关系
局部坐标->全局坐标
RtPt=P,此时Rt是R的逆,这才是正确的,但是由于R的转置*R=单位阵,因此使用转置取代求逆操作,也就是说,此时的Rt是特征向量作为列组成的。所以出现
obb_position_ = mean_value_ + obb_rotational_matrix_ * shift;
obb_position_ 就是OBB包围盒中心的全局坐标。
第二点:
obb_min_point_.x -= shift (0);obb_min_point_.y -= shift (1);obb_min_point_.z -= shift (2);obb_max_point_.x -= shift (0);obb_max_point_.y -= shift (1);obb_max_point_.z -= shift (2);
obb_min_point_和obb_max_point_减去包围盒中心点坐标是什么意思?
经过测试发现,减去中心点坐标之后,包围盒的坐标是存在问题的
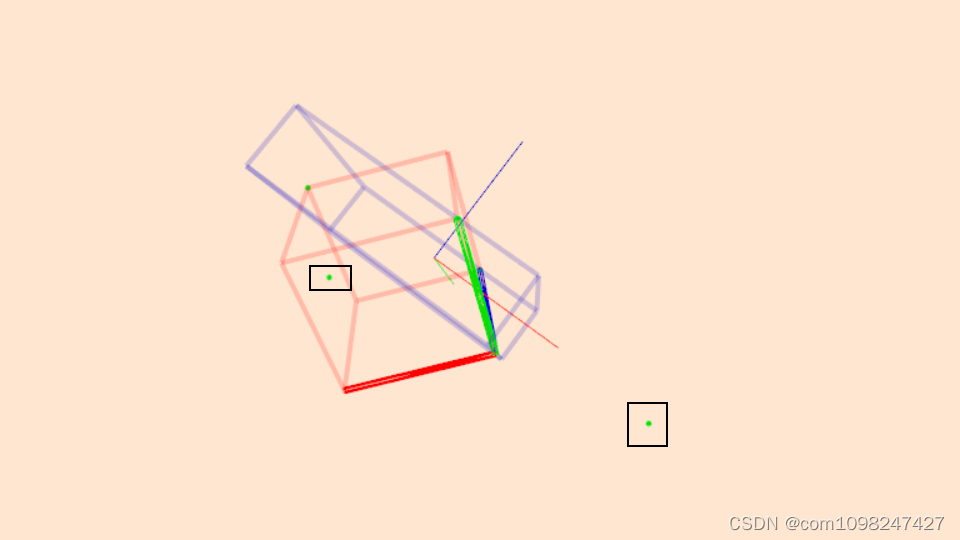
如上图所示,两个黑色框中的点就是获取的包围盒的最小点和最大点,这里明显可以看出,这两点和显示的OBB包围盒没有关系,是有问题的。
因此绘制正确的OBB包围盒时,采用的是给定包围盒中心的坐标和包围盒的宽度和长度的方法进行绘制。
欢迎留言。