一、接雨水

题目链接

题目描述：

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

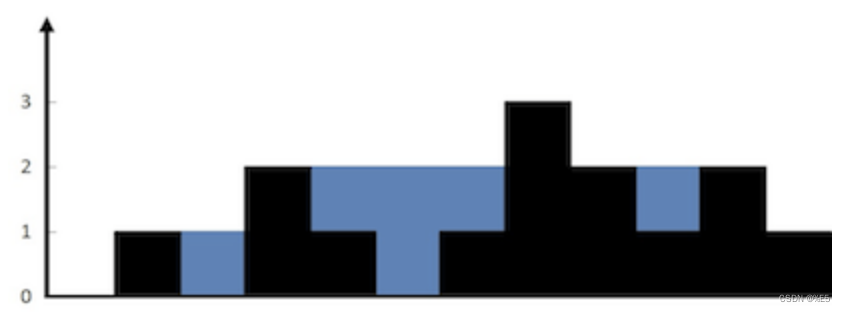
输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

示例 2：

输入：height = [4,2,0,3,2,5]
输出：9

方法一：按列求（动态规划）

我们把每一列能接的水加起来即可，而每一列的水只取决于当前列左边的最高墙和右边的最高墙。
根据木桶效应，在左边和右边取低的那一个，然后减去当前列的高度即可求出当前列的接水量。
这样我们就可以创建两个数组，一个记录包括当前列左边的最高墙，一个记录包括当前列右边的最高墙，采用动态规划的思想。
为什么要包括当前列？

首先可以解决边界问题，其次如果当前列是左边最高的或者右边最高的，那么减去自己的高度就是0。

class Solution {
public:int trap(vector<int>& height) {int n = height.size();vector<int> leftMax(n), rightMax(n);int Max = 0;for(int i = 0; i < n; i++){if(height[i] > Max){Max = height[i];}leftMax[i] = Max;}Max = 0;for(int i = n - 1; i >= 0; i--){if(height[i] > Max){Max = height[i];}rightMax[i] = Max;}int sum = 0;for(int i = 0; i < n; i++){sum += min(leftMax[i], rightMax[i]) - height[i];}return sum;}
};

方法二：双指针

上面我们说过只用看左右两边最高墙中的最小值即可，所以现在我们定义两个指针，left从左向右，right从右向左，每次让小的那一列墙的指针向中间移动（因为我们不关心左边最高墙和右边最高墙中的高的那列墙）。

class Solution {
public:int trap(vector<int>& height) {int n = height.size();int leftMax = 0, rightMax = 0;int left = 0, right = n - 1;int sum = 0;while(left <= right){if(height[left] < height[right]){leftMax = max(leftMax, height[left]);sum += leftMax - height[left];left++;}else{rightMax = max(rightMax, height[right]);sum += rightMax - height[right];right--;}}return sum;}
};

方法三：单调栈

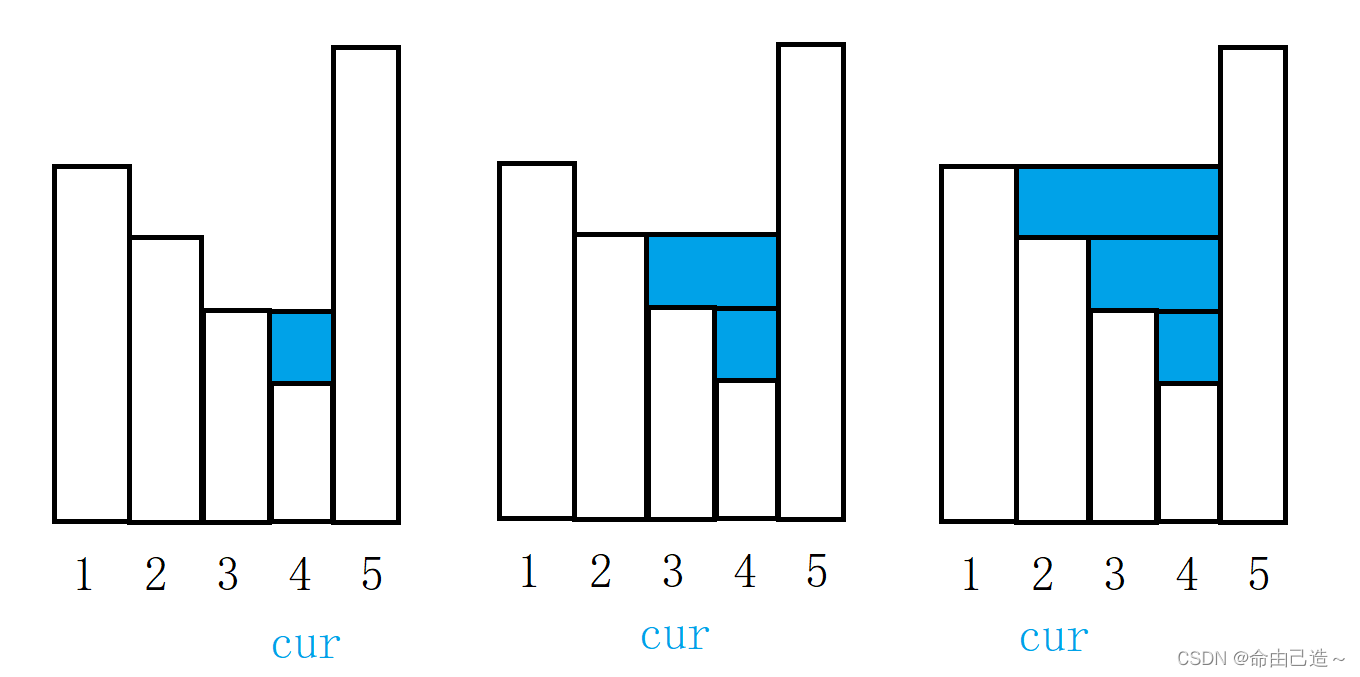
用一个极端场景来举例子：

如果是单调递减的就依次入栈，直到碰到比栈顶元素要高的墙，此时就依次判断前面入栈且比当前墙要低的元素。

比方说现在到5下标。此时依次出栈之前的元素来计算接水量：

class Solution {
public:int trap(vector<int>& height) {int n = height.size();stack<int> st;int sum = 0;for(int i = 0; i < n; i++){while(!st.empty() && height[i] > height[st.top()]){int cur = st.top();st.pop();if(st.empty()){break;}int len = i - st.top() - 1;sum += (min(height[st.top()], height[i]) - height[cur]) * len;}st.push(i);}return sum;}
};

二、直方图最大矩形面积

题目链接

题目描述：

给定非负整数数组 heights ，数组中的数字用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。
求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1:

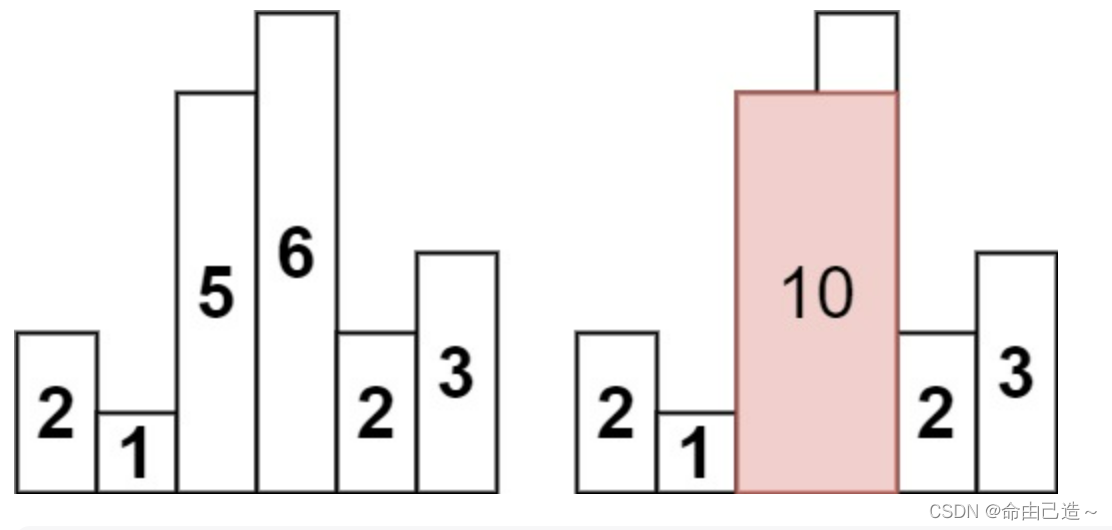
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

示例 2：

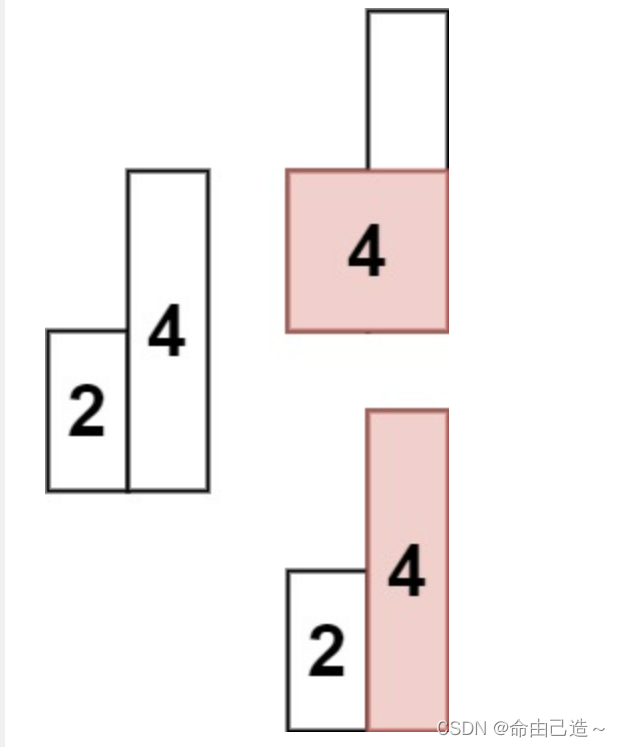
输入： heights = [2,4]
输出： 4

思路分析：

单调栈

这道题可以类比上面的接雨水问题，我们也可以用单调栈的方式来求解。
栈里面存的是下标，主要是用来计算宽度。
遍历每个下标，如果当前列大于栈顶元素，就继续入栈，如果小于栈顶元素，进行处理：

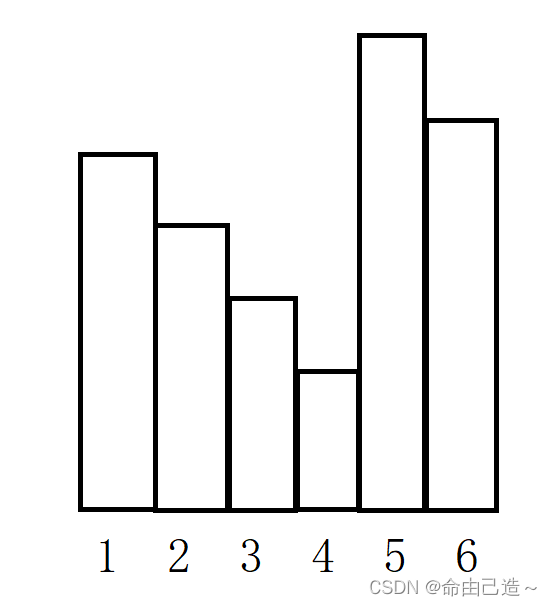
从1开始遍历，当遍历到1的位置时还不能确定1位置是不是最大的矩形面积，继续向后遍历，当遍历到2的位置时，就可以确定2之前的的大面积了。

如果已经确定了一个柱形的高度，我们可以无视它（出栈）。

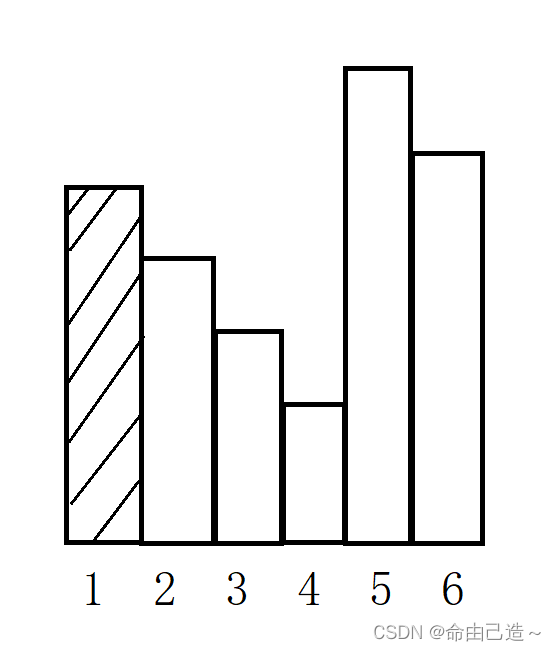
为什么可以无视呢？
后边的元素一定比1要小，所以当要求最大面积的时候一定会跨过第一列：

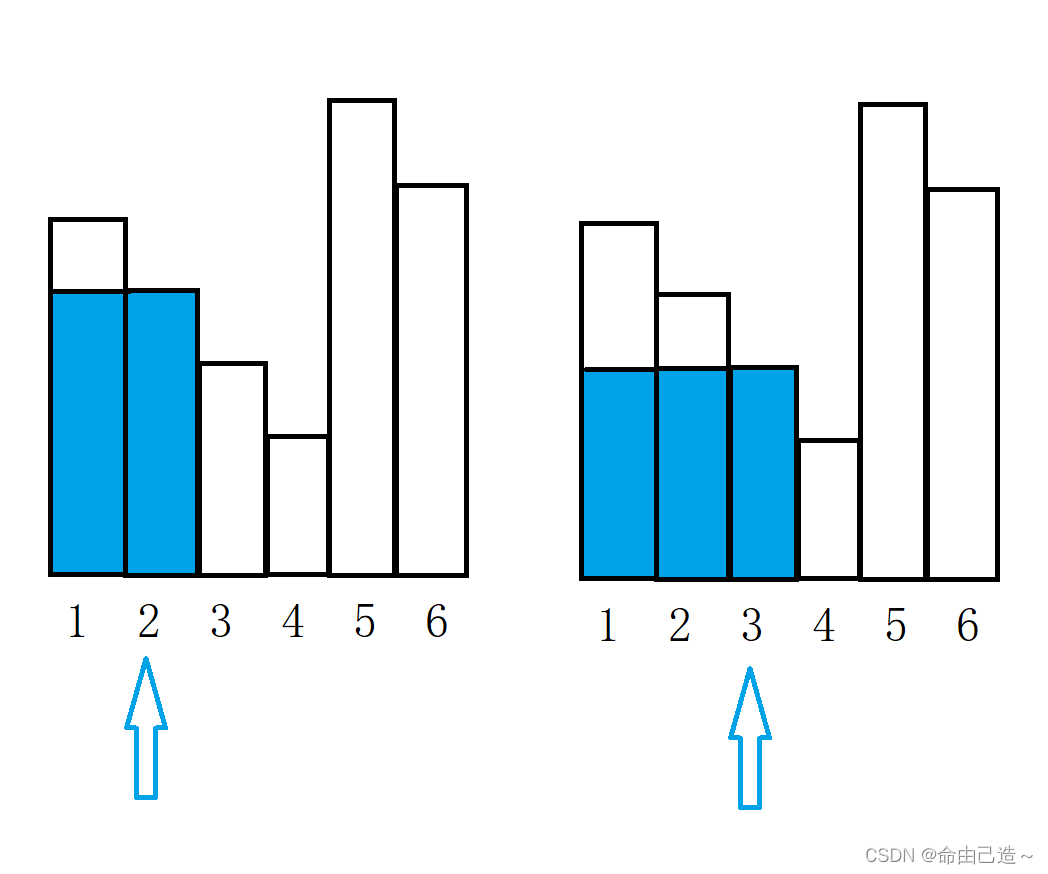
就算1前面也有元素也是可以可以直接跨过。
可以看到2不用关注1，3不用关注1和2。

这里还有两个特殊的情况：
1️⃣ 弹栈的时候，栈为空；
2️⃣ 遍历完成以后，栈中还有元素；

如果弹栈的时候栈为空，那么说明宽度要从当前位置一直延伸到0下标。
如果遍历完后栈中还有元素。比如说这个图：

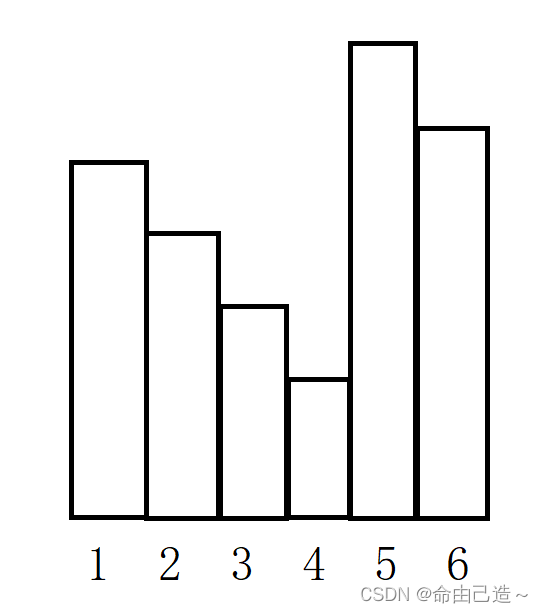
最后剩下的就是4和6，对于4和6，先处理6在处理4：

class Solution {
public:int largestRectangleArea(vector<int>& heights) {int n = heights.size();stack<int> st;int ans = 0;for(int i = 0; i < n; i++){while(!st.empty() && heights[i] < heights[st.top()]){int mid = st.top();st.pop();int w = i;if(!st.empty()){w = i - st.top() - 1;}ans = max(ans, w * heights[mid]);}st.push(i);}while(!st.empty()){int mid = st.top();st.pop();int w = n;if(!st.empty()){w = n - st.top() - 1;}ans = max(ans, w * heights[mid]);cout << w * heights[mid] << endl;}return ans;}
};

哨兵位优化

为了处理上面两个特殊情况，我们可以在首位都添加一个0。

class Solution {
public:int largestRectangleArea(vector<int>& heights) {heights.insert(heights.begin(), 0);heights.push_back(0);int n = heights.size();stack<int> st;st.push(0);int ans = 0;for(int i = 1; i < n; i++){while(heights[i] < heights[st.top()]){int mid = st.top();st.pop();int left = st.top();int right = i;int w = right - left - 1;ans = max(ans, w * heights[mid]);}st.push(i);}return ans;}
};

三、矩阵中最大的矩形

题目链接

题目描述：

给定一个由 0 和 1 组成的矩阵 matrix ，找出只包含 1 的最大矩形，并返回其面积。
注意：此题 matrix 输入格式为一维 01 字符串数组。

示例 1：

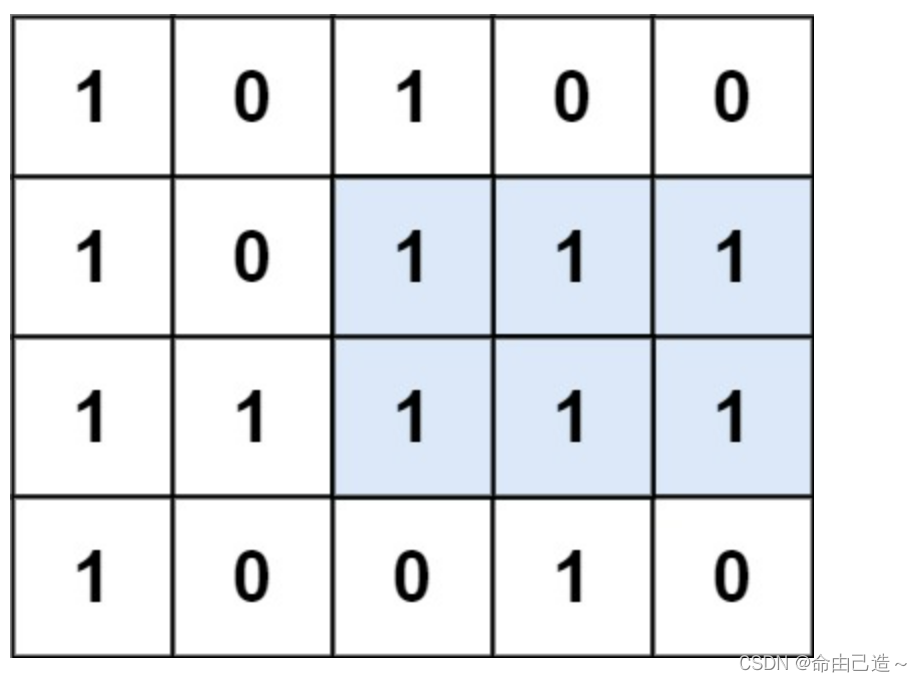
输入：matrix = [“10100”,“10111”,“11111”,“10010”]
输出：6
解释：最大矩形如上图所示。

示例 2：

输入：matrix = []
输出：0

示例 3：

输入：matrix = [“0”]
输出：0

示例 4：

输入：matrix = [“1”]
输出：1

示例 5：

输入：matrix = [“00”]
输出：0

思路分析：
例如上面的图，我们可以分层看，每一层都是求直方图最大矩形面积。

第一层柱状图的高度[“1”,“0”,“1”,“0”,“0”]，最大面积为1；
第二层柱状图的高度[“2”,“0”,“2”,“1”,“1”]，最大面积为3；
第三层柱状图的高度[“3”,“1”,“3”,“2”,“2”]，最大面积为6；
第四层柱状图的高度[“4”,“0”,“0”,“3”,“0”]，最大面积为4；

这道题的解法就是前缀和+单调栈

前缀和+单调栈

class Solution {
public:int largestRectangleArea(vector<int>& heights) {int n = heights.size();stack<int> st;st.push(0);int ans = 0;for(int i = 1; i < n; i++){while(heights[i] < heights[st.top()]){int mid = st.top();st.pop();int left = st.top();int right = i;int w = right - left - 1;ans = max(ans, w * heights[mid]);}st.push(i);}return ans;}int maximalRectangle(vector<string>& matrix) {if(matrix.size() == 0) return 0;int res = 0;vector<int> v(matrix[0].size() + 2);for(int i = 0; i < matrix.size(); i++){for(int j = 0; j < matrix[i].size(); j++){if(matrix[i][j] == '1'){v[j + 1] += 1;}else{v[j + 1] = 0;}}res = max(res, largestRectangleArea(v));}return res;}
};

---

---