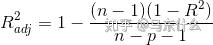回顾线性回归的公式:θ是系数,X是特征,h(x) 是预测值。
h(x) = θ0 + θ1x1 + θ2x2 + … + θnxn
h(x) = Σ θixi( i=0~n )
h(x) = θTX = [θ1,θ2,θ3,…,θn] * [x1,x2,x3,…,xn]T
最终要求是计算出θ的值,并选择最优的θ值构成算法公式,使预测值能够尽可能接近真实值。
求解线性回归的思路
线性回归主要用到两种方法:最大似然估计、最小二乘法。两种思路截然不同,但最终得到的结果是一致的。
1、最大似然估计求解

所有样本的误差ε(i) (1 ≤ i ≤ n) 是独立同分布的,服从均值为 0,方差为某个定值的 б2 的高斯分布。
解释一下上面这个概念。
a、独立同分布( i.i.d )
实际问题中,很多随机现象都可以看做 独立影响的综合反映,往往服从正态分布。
特征X:x1~xn 是独立同分布的。
每一个样本根据特征计算出的预测值和真实值之间的误差:ε1~εn 也是独立同分布的。
概率论中的一个概念,即一组数据彼此时间互不干扰,在现实环境里随机出现。
独立:比如抛硬币,每次硬币落地这一事件都是独立的,不会因为之前抛硬币的结果而改变。而如果是从一堆白球中每次取一个黑球这种事件,由于随着白球的减少下次取出黑球的概率会不断变大,则不能称每次的取球行为相互独立。
同分布:如果一组数据都是从掷6面色子的结果中获取的,则称样本同分布。如果数据中夹杂着几个掷12面色子的结果,则样本不是同分布的。
b、高斯分布
也称为正态分布,正态曲线呈钟型,两头低,中间高,左右对称因其曲线呈钟形,因此人们又经常称之为钟形曲线。
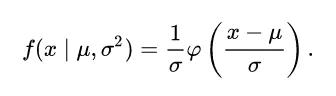
若随机变量X服从一个数学期望为μ、方差为σ2的正态分布,记为N(μ,σ2)。其概率密度函数为正态分布的期望值μ决定了其位置,其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。
所有样本的误差ε(i) 服从均值为0,方差为σ2: 因为我们最终得到的公式是一个相对完美的公式,所以实际值会均匀得落到公式的两侧,如下所示。所有实际值和预测值的误差均值是0,均值为0意味着误差形成的高斯分布是一个

c、中心极限定理
中心极限定理:只要x1~xn 是独立同分布的,那么y = x1+x2+…+xn;
则y服从:均值 = n * (x1~xn 的均值) = nμ;方差 = n*(x1~xn的方差)=nσ2;
∵ 每个样本的预测值和实际值之间的误差ε(i)也是独立同分布的,所以所有误差的和 ε(i) 满足上述的定义。
又∵ 误差的均值为0,这点在b高斯分布中已证明。(模型是最优的,所以所有的实际值必然均匀得落在预测值的上下两侧,最后误差的均值是0)
∴ 所有样本的误差ε(i) (1 ≤ i ≤ n) 是独立同分布的,服从均值为 0,方差为某个定值的 б2 的高斯分布。得证。

似然函数定义
设: f (x | θ) 为样本 X=x1,x2,x3,…xn)的联合概率密度函数,如果观测到的X=x,则称θ的函数:L ( θ | x) = f (x | θ) 为似然函数。
即给定样本x情况下,产生参数θ的可能性 = 在给定参数θ的情况下,观测到样本x的概率。
因此: 
联合概率密度的值等于似然函数的值。
如果X是离散的随机变量,似然函数 L (θ | x) = p θ (X=x)
比较似然函数在某个参数点处的取值,
如果:p θ1 (X=x) = L (θ1 | x),p θ2 (X=x) = L (θ2 | x);
其中:p θ1 (X=x) > p θ2 (X=x) 即 L (θ1 | x) > L (θ2 | x);
则:当θ = θ1时观测到X=x的可能性大于θ = θ2时,说明θ1比θ2更像是θ的真实值。
上面解释得比较偏于理论,用一个例子来进一步解释
1号背包:白球1个 黑球99个 ,显然取得黑球的概率是99%;
2号背包:白球99个 黑球1个,显然取得黑球的概率是1%;
现在我被蒙上眼睛,在某个背包中取出了一个黑球。那么问题来了,我最有可能是从哪个背包中取出黑球的?显然刚才我从1号背包中取球的概率较大。
题干中,黑白两种球取出来的概率就是参数值 θ 。观测值是黑球,对应的公式为:
p θ1 (X=x) = L (θ1 | x) > L (θ2 | x) = p θ2 (X=x) ;
p θ1 (X=黑球) ; 背包1从中取得黑球的概率为99%;
p θ2 (X=黑球) ; 背包2中取得黑球的概率为1%;
上述例子中的θ只有背包1和背包2两种参数,但在实际中可能会出现很多组θ:( θ1,θ2,θ3,…,θn)




最大似然函数求解θ过程
理论知识补充完了,接下来先回到最初的式子:
y(i)= θTX (i) + ε(i);实际值=预测值+误差;
即 ε(i) = y(i) - θTX (i) ①
由于误差是服从高斯分布的,高斯分布的概率密度函数:
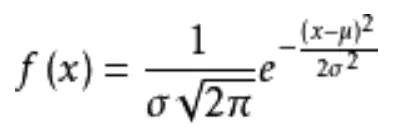
正态分布的概率密度函数
由于 ε(i) 均值为0,将 ε(i) 代入公式得②:

② 第i个观测值对应的误差的概率密度函数
将公式 ε(i) = y(i) - θTX (i) ① 代入概率密度函数②得③:

如何从②转化到③是最难理解的一步。
首先需要理解的是, ε(i) = y(i) - θTX (i),只有在给定了x的情况下,y才有取值的可能。
p(x;θ),在给定了θ情况下x的取值;
p(y|x;θ),在给定了x的情况下,还给定了某种参数θ的情况下,y的概率密度函数是多少;
由于x和θ是一个定值,所以θTX (i)可以理解成才一个定值C。
接着思考随机变量 ε(i),误差期望值(均值)是0, E(ε(i)) = 0 => E(ε(i)+C) = C
ε(i)是服从正态分布的(高斯分布),ε(i)+C是一个服从均值为C,方差不变的正态分布。
所以:既然y(i)= θTX (i) + ε(i);y也是服从一个均值为(均值=θTX (i),方差= ε(i)的方差)的正态分布的。但是有一个前提条件:X和θ是被给定的。

所以公式③左侧的含义:在给定了x和某种参数θ的情况下y的概率密度函数。
∵ 联合概率密度函数等于似然函数,L ( θ | x) = f (x | θ);
∴ 得出公式④

联合概率密度函数等于似然函数
联合概率密度函数是怎么得到的?
∵ ε(i)是独立同分布的;
又∵ y(i)也是独立同分布的;
又∵ 根据概率公式: P(AB)表示A和B同时发生的概率;如果A、B相互独立 则P(AB)=P(A)*P(B);
∴ 将公式③左侧进行连乘,得到了公式④上行的右半部分;进一步展开即可得到公式④下行的结果。
到目前为止④联合概率密度函数等于似然函数是我们得出的结果,以上的叙述可以帮你很好的理解似然函数的概念。
总结几个容易混淆的概念
1、f(x|θ) 是什么?
f(x|θ) 是联合概率密度函数,是我所有样本基础上的某个事件是否发生的联合概率密度函数。
2、换个角度再解释下面这个公式:

以上的式子,是发生在单个样本情况下服从的一个正态分布。
即p(y(1)|x(1);θ)…p(y(m)|x(m);θ) 都服从以上式子的正态分布。
所以他们的联合概率密度函数就是1~m个正太分布公式的连乘。
理论依据:y(i)是独立同分布的。
3、L(θ|x) = f(x|θ)
即给定样本x情况下,产生参数θ的可能性 = 在给定参数θ的情况下,观测到样本x的概率。
L(θ|x) 后面统一简写为L(θ),即最大似然函数 ,看它取得最大值时对应的参数θ是多少。
现在似然函数已经求完了,接下来我们要求L(θ) 是最大值情况下的 θ 的值。
首先考虑公式④的求导,显然不太好求。

但我们知道对于任意一个变量,对它取对数,log(x)、ln(x),它们的单调性和x的单调性是一样的。随着x的增大,对数函数也增大,x减小,对数函数也减小。所以如果考虑求最大值,log(L( θ)) 、L(θ)它们极值点对应的自变量θ所在的位置是一样的。
根据结论推导出如下公式:

看公式的最后一行,减号左边的式子是一个常数,要取整个式子的最大值,就是求后面这部分式子的最小值。
所以现在问题转化为求如下式子最小值时θ的值:
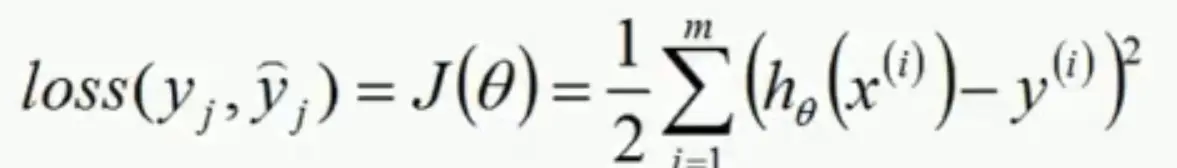
该函数就是我们线性回归中最后需要求解的目标函数。
讲到这里又需要引入一个新的概念:损失函数(代价函数)
在机器学习中,我们希望找到一个面向整个模型的度量函数,使得这个度量函数越小越好。
本来我们求的是似然函数的最大值,现在把问题转换成了求目标函数的最小值。
损失函数:衡量的是单个观测值在当前系统下的一个损失情况。
代价函数:衡量所有样本在当前系统下的损失情况。
总结一下求解最大似然估计的步骤:
1、写出似然函数L(θ)
2、对似然函数取对数,并整理 ln L(θ)
3、求导数
4、解方程-导数为0的点(极值) ∂ ln L(θ) / ∂ θ = 0
好了,实在听不懂就算了,后文讲解一个更简单的求解θ的办法:最小二乘求解。
03 回归算法 - 线性回归求解 θ(最小二乘求解)
20210511
https://www.jianshu.com/p/662076060e44?from=singlemessage
https://www.jianshu.com/p/662076060e44
最小二乘法
https://zhuanlan.zhihu.com/p/87582571
https://www.jianshu.com/p/d4809616b131
最小二乘法 矩阵推导