1695_week2_算法与函数（MIT使用Python编程学习手记）

全部学习汇总： GreyZhang/python_basic: My learning notes about python. (github.com)

首先说明一下，这部分信息的整理只是我个人的理解。由于自己的知识功底以及英语水准，很可能会有大量的疏漏。再此，我只想把自己学习时候的一点收获整理分享一下。如果能够给别人一点点帮助，荣幸之至。如果有错误，也请予以斧正。如果感觉我有描述不清的，当然也可以跟我邮件交流。由于直接复制代码排版上会有很多问题，稳文中代码全都截取VIM编辑器的界面展示。如果需要代码可以给我发邮件索取，以下是我的联系方式：

Email : greyzhang@126.com

这部分学习需要有一定的Python学习基础了，需要掌握的概念大致有以下几个：

Python的语法、Python的数据类型（整形、浮点、元组、列表、字典等）。有一个数据类型需要单独拿出来强调一下，那就是布尔量。接下来的很多判断或者程序分支的概念会建立在最一个布尔量的判断基础上。

在之前的学习手记中已经总结了一部分Python的语句操作，我们可以通过在Python shell中年输入一系列的语句来实现某个功能。看起来，我们是让计算机运行了我们的软件功能，但是功能肯定是远远不够。

迭代

在程序设计中，一个很重要的算法概念便是迭代。通过迭代，我们可以反复重用同一段代码来解决我们的问题。通过程序语言对我们需要处理的信息进行描述，然后再迭代的程序段中反复执行我们写好的一段程序，在执行的过程中通过对布尔量的查看判断来确认我们是否找到一个合适的结果。这是对“猜想——验证”的计算机思考方法的一种实践尝试。

接下来通过一个简单的小例子来说明一下：通过Python实现求解一个正整数点额平方。

代码如下：

这里我们用到了while循环，while循环最简单的结构如下：

While <判断条件>：

循环体

以上程序的执行结果：

>>> ================================ RESTART ================================

>>>

3*3 = 9

如果改变x的数值，可以得到你想要的不同结果。比如改成12345，执行结果如下：

>>> ================================ RESTART ================================

>>>

12345*12345 = 152399025

虽说此处还谈不上代码的优化，使用Python可以有更好的实现方法。但是可以看出的式程序执行速度还是很快的，一瞬间就可以得出你想要的结果。

猜想——验证

“猜想——验证”是计算机思维的一种常用的方法，我们假定一系列的可能性然后一次次验证，最终判断是否有我们想要的结果。

通过一个简单的例子来说明一下：寻找一个整数是否存在整数立方根。

我们可以从0开始，直到这个数本身为止一次次查看猜测数值的三次方是否等于给出的整数。如果找到那就寻找到了这个数的整数立方根，如果找不到，那这个数肯定是没有整数立方根。

设计代码如下：

执行结果如下：

>>> ================================ RESTART ================================

>>>

input a number:123

can't find %d's cube root

>>> ================================ RESTART ================================

>>>

input a number:27

cube root of 27 is: 3

通过以上的例子可以看出“猜想——验证”方法的大致步骤：

1，给出初始的猜想

2，在循环的结构中不断验证，如果满足条件则终止，因为找到了我们要的答案。如果不满足验证条件，那么在循环结构中改变猜想再次验证。

常用迭代的特点：

通过以上几个例子大致可以总结出常用迭代程序的特点：

1，有一个状态变量

a,在循环体外进行初始化

b,在循环体中改变状态量

c,判断验证的依据来自于状态量的变化

2，状态量递减：

A,初始化的数值为整数

B,执行的时候整数非负

C,<=0的时候结束

D,在循环中递减

以上特点并不是所有迭代程序的特征，但是是常用迭代程序一般都有的特点。如果满足以上特点的迭代程序，我们可以通过看状态量的数值来弄清楚我们程序的执行度。由于规律递减的存在，我们很清楚就能够知道到底还有多少没有执行完。

For循环：

While循环通常可以用来对一系列信息进行验证，如同我们前面看到的数字。在Python中，对这种情况的处理还有另外一种特殊的方式叫做for循环。

For循环的结构入下：

For <判断条件> :

循环体

在for循环中，循环的状态量首先被绑定为序列中的第一个元素，然后执行循环体程序。循环体执行结束后，状态量绑定为第二个元素，执行循环体程序，一直这样执行下去。如果遇到break，循环会直接终止。

如果想使用一系列连续的数字序列，可能会用到Python的内置函数range(n)。这个函数可以用来产生0到n-1的连续数字序列。函数是重载的，针对不同的需要也可以有更加方便的使用方式。

下面使用for循环实现上面的cube root功能：

执行结果如下：

>>> ================================ RESTART ================================

>>>

input a number:27

cube root of 27 is 3

>>> ================================ RESTART ================================

>>>

input a number:-27

cube root of -27 is -3

>>> ================================ RESTART ================================

>>>

input a number:123

123 is not a perfect cube

以上代码不仅完成了与之前while循环相同的功能，而且同时支持负数的判断。

浮点数的处理;

首先看一下十进制的表示：

302 = 3*10**2 + 0*10**1 + 2*10**0

为什么我们的祖先首先采用的是十进制的计数方式呢？那是因为我们有十根手指头，但是计算机没这个。计算机知道的就只有开或者关两种状态，只知道0或者1。

这样，用二进制表示一个十进制的例子如下：

10011 = 1*2**4 + 0*2**3 + 0*2**2 + 1*2**1 + 1*2**0

（用十进制表示是19 = 16 + 2 + 1）

在计算机的内部，数字是以二进制的形式才存储的。考虑一下10011除以2后的表达方式，实际上可以表示为：1*2**3 + 0*2**2 + 0*2**1 + 1*2**0。如果在计算机中进行除以2的操作，实际上是把二进制的数值向右移动了一位。

把这思考的一切用Python处理展示出来，可以设计如下的代码：

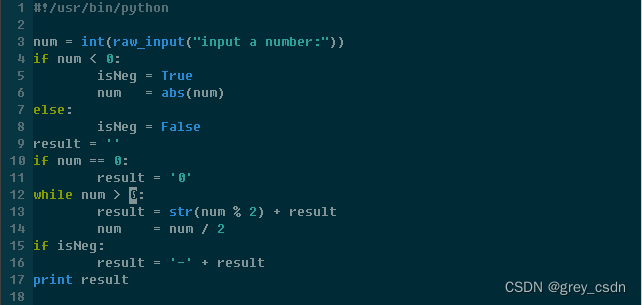
执行效果如下：

>>> ================================ RESTART ================================

>>>

input a number:19

10011

>>> ================================ RESTART ================================

>>>

input a number:-19

-10011

如果考虑到分数会是怎么样呢？

3/8 = 0.375 = 3*10**(--1) + 7*10**(-2)+5*10**(-3)

0.375 * (2 ** 3) = 3（十进制）

转换为二进制：11

除以（2**3），也就是右移三位：0.011（二进制）

设计代码如下：

代码执行结果如下：

>>> ================================ RESTART ================================

>>>

Enter a decimal number between 0 and 1: .375

Remainder = 0.375

Remainder = 0.75

Remainder = 0.5

011

.011

The binary representation of the decimal 0.375 is .011

>>> ================================ RESTART ================================

>>>

Enter a decimal number between 0 and 1: .1

Remainder = 0.1

Remainder = 0.2

Remainder = 0.4

Remainder = 0.8

Remainder = 0.6

Remainder = 0.2

Remainder = 0.4

Remainder = 0.8

Remainder = 0.6

Remainder = 0.2

Remainder = 0.4

Remainder = 0.8

Remainder = 0.6

Remainder = 0.2

Remainder = 0.4

Remainder = 0.8

Remainder = 0.6

Remainder = 0.200000000001

Remainder = 0.400000000001

Remainder = 0.800000000003

Remainder = 0.600000000006

Remainder = 0.200000000012

Remainder = 0.400000000023

Remainder = 0.800000000047

Remainder = 0.600000000093

Remainder = 0.200000000186

Remainder = 0.400000000373

Remainder = 0.800000000745

Remainder = 0.60000000149

Remainder = 0.20000000298

Remainder = 0.40000000596

Remainder = 0.800000011921

Remainder = 0.600000023842

Remainder = 0.200000047684

Remainder = 0.400000095367

Remainder = 0.800000190735

Remainder = 0.60000038147

Remainder = 0.200000762939

Remainder = 0.400001525879

Remainder = 0.800003051758

Remainder = 0.600006103516

Remainder = 0.200012207031

Remainder = 0.400024414062

Remainder = 0.800048828125

Remainder = 0.60009765625

Remainder = 0.2001953125

Remainder = 0.400390625

Remainder = 0.80078125

Remainder = 0.6015625

Remainder = 0.203125

Remainder = 0.40625

Remainder = 0.8125

Remainder = 0.625

Remainder = 0.25

Remainder = 0.5

0001100110011001100110011001100110011001100110011001101

.0001100110011001100110011001100110011001100110011001101

The binary representation of the decimal 0.1 is .0001100110011001100110011001100110011001100110011001101

关于不能够表示为num/(2 ** n)的这种形式，判断结束条件当然不能够以能够整除为条件。因为数据的存储在计算机中的位数是有限制的。在一定精度内，这种判断可以使用一个比较小的精度值与之比较作为结束的判断条件。

常用的算法：

逐次逼近

1，选择合适的步长

太小计算时间长

太大可能计算不出结果

2，给出一个最小精度作为判断条件

二分查找

1，选择中间数

判断

根据判断决定是否再次二分查找

结束条件：达到允许精度

2，特点

缩短周期

更加智能化

适合处理有序序列

牛顿-莱布尼茨

1，g - p(g)/p’(g)是多项式方程的猜想更优解

2，特点：

高效

需要数学处理作为前提

求解平方根：

逐次逼近法：

执行结果：

>>> ================================ RESTART ================================

>>>

root of number 25.000000 is 4.999000

>>> ================================ RESTART ================================

>>>

root of number 24.000000 is 4.897959

结果还算是精确，由于步长选择比较小运算时间较长。

二分查找：

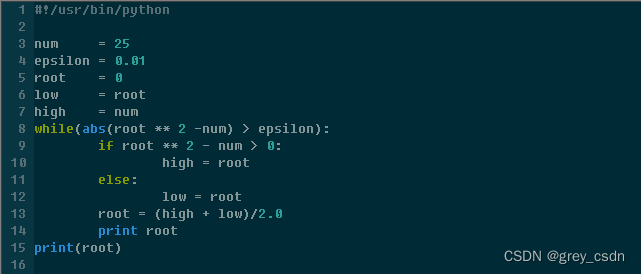
执行结果：

>>> ================================ RESTART ================================

>>>

12.5

6.25

3.125

4.6875

5.46875

5.078125

4.8828125

4.98046875

5.029296875

5.0048828125

4.99267578125

4.99877929688

5.00183105469

5.00030517578

牛顿-莱布尼茨：

执行结果：

>>> ================================ RESTART ================================

>>>

13.0

7.46153846154

5.40602696273

5.01524760194

5.00002317825

尝试做一个复杂运算，求12345的平方根：

关于迭代的概括：

1，用相同的方法反复验证>>> ================================ RESTART ================================

>>>

6173.0

3087.499919

1545.74914984

776.867784296

396.37925959

213.761837095

135.756512451

113.345688237

111.130142813

111.108057708

11次迭代便得出一个很好的解，足以看出算法优秀的重要性。如果采用逐次逼近，这将会是很大的工作量。

2，猜测的方式可以灵活使用多种算法。

函数：

关于函数，解决的问题不仅仅是功能的重用还有一个功能的抽象。函数可以把一个功能抽象出来，让其他人在不需要考虑函数的实现细节的基础上使用它。这种抽象可以称之为黑盒抽象，这不仅让代码重用变得更加简单也让代码的调试变得更加容易。

能够开始学习函数的设计，需要有基本的Python语言知识以及循环结构的了解，这些之前已经整理。之前的循环结构的确是能够在一定程度上解决代码重用的问题，但是解决的不够完美，如果我们需要重复多个循环那我们需要把整个循环体代码拷贝多次。这也带来了另外一个问题——变量的管理以及代码修改的困难。很可能我们使用的多个拷贝代码段中的变量会相互影响，当需要改变某一个语句的时候我们也可能需要修改多次。函数在使用上则要比这方便的多。

下面在举例演示一下函数的使用，通过一个简单的函数实现求两个数值中的最大值。

代码如下：

在IDLE中load之后，运行效果如下：

>>> ================================ RESTART ================================

>>>

>>> MaxNum(223,112)

223

>>> MaxNum(-6,-10)

-6

>>> x = 1

>>> y = 2

>>> MaxNum(123,456)

456

>>> MaxNum(x,y)

上面不仅能够看到代码可以重用，结果不受上次调用的影响，而且能够看到在IDLE环境中的x，y的赋值不会影响到函数中的x和y的数值。这是因为函数有着自己独立的变量空间，而且互不影响。关于每次调用的互不影响，递归的算法可以很好地说明，这个后面有时间在做整理。关于独立的变量空间，可以把上面的代码修改一下，如下：