用多边形顶点的逆时针序列表示凸多边形，即P={v0,v1,…,vn-1}表示具有n条边的凸多边形。

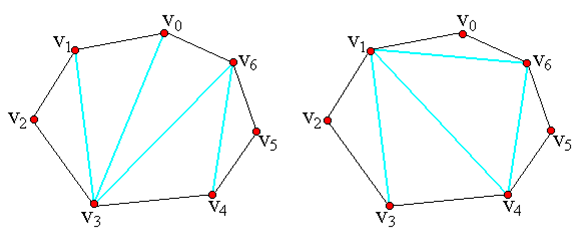
给定凸多边形P，用互不相交的弦将P分为一个个的三角形,称为凸多边形三角剖分。

然后，定义多边形的边和弦组成的三角形上的权w（本题定义三角形的权为边长之和）。要求确定该凸多边形的三角剖分，使得该三角剖分中诸三角形上权之和为最小，则称其为凸多边形P的最优三角剖分。

输入格式:

第一行一个n,表示有n个顶点（n<20）。

接下来n行，每行两个小数，分别表示该点的横坐标和纵坐标。

输出格式:

一个小数，表示最优三角剖分后，所有三角形的边长和的和最小值，小数点后保留2位。

输入样例:

4
1.0  1.0
4.0  1.0
4.0  5.0
1.0  5.0

输出样例:

24.00

#include <iostream>
#include <iomanip>
#include <vector>
#include <cmath>
#include <limits>using namespace std;struct Point {double x, y;
};double distance(const Point &a, const Point &b) {return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}double optimalTriangulation(int n, const vector<Point> &points) {vector<vector<double>> dp(n, vector<double>(n, 0));for (int gap = 2; gap < n; gap++) {for (int i = 0; i + gap < n; i++) {int j = i + gap;dp[i][j] = numeric_limits<double>::max();for (int k = i + 1; k < j; k++) {double sum = distance(points[i], points[j]) +distance(points[i], points[k]) +distance(points[j], points[k]);double cost = dp[i][k] + dp[k][j] + sum;dp[i][j] = min(dp[i][j], cost);}}}return dp[0][n - 1];
}int main() {int n;cin >> n;vector<Point> points(n);for (int i = 0; i < n; i++) {cin >> points[i].x >> points[i].y;}double answer = optimalTriangulation(n, points);cout << setprecision(2) << fixed << answer << endl;return 0;
}