进入正题前，先来复习下关于2次幂的mod运算
设n为2次幂，数a mod n 等价于 a & n-1
从二进制来看，相当于余数为a省去n最高位左侧的所有位(含最高位)，保留n右侧所有低位即为余数
如：a = 7(0000_0111),n=4(0000_0100),通过7 & (4-1) 即0000_0111 & 0000_0011 结果为3（0000_0011）

dictScan方法中，对游标计算下表用了一个位逆序运算的方法，总体的算法如下：

        v |= ~m0;/* Increment the reverse cursor */v = rev(v);v++;v = rev(v);

在分析这个算法前，我准备先大概说下这个算法的目的：

1、首先这里有个前提，即dict的长度都是2的幂，且每次扩容都是扩大一倍，即size1 = size0*2。
扩容前，某个下标idx的若干数据，其实就是key mod size0后同余数idx若干key,在扩容后，因为是扩大一倍，因此这些同余的key，就会分为两部分，idx，和idx+size0的两部分。

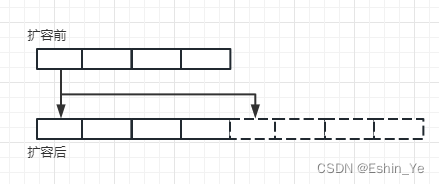
2、遍历的时候，如果没有扩容，那么所有的数据，都在旧的空间里，只需要遍历旧的空间ht[0]即可，但是如果扩容了，那么已遍历过的下标的数据，可能有部分会分配到idx+size0的位置，如果按下标顺序遍历的话，可能会大量遍历到重复的数据。

假设扩容前空间长度为4，在遍历完idx为0的数据后，发生了扩容，空间扩大到8，，那么原本idx为0的数据，在扩容后，idx就调整为0+4==4，那么新空间idx为4的数据，都是已经遍历过的数据

3、如何尽可能减少数据的重复遍历呢，是不是可以考虑调整遍历的顺序，从而实现扩容后的遍历，跳过新空间中idx+size0下标的位置：

当size=2：
遍历的下标有：0,1

扩容后size=4：
那么原本0下标的数据，在新空间就对应：0，2
原本1下标的数据，在新空间就对应：1, 3
那么按0,2,1，3的顺序遍历，则可在扩容后，跳过已经遍历的数据。

扩容后size=8：
那么按原size=4：0,2，1,3的顺序，新扩容后的空间对应关系就有：
0对应新空间：0，4
2对应新空间：2，6
1对应新空间：1, 5
3对应新空间：3, 7
那么此时的遍历顺序则为0,4，2,6，1,5，3,7

因此，遍历的逻辑为，给定一个下标，在新size下的访问顺序，要按旧size做为模同余的key的顺序进行遍历，二进制的演进如下：
（以下：cursor % size 余数idx小于size/2的称为低位槽，大于或等于size/2小于size的称为高位槽; 掩码位： 即数a，与掩码位数相同的位。）
当size为2时，掩码为1，二进制表示为1，掩码位只有一位；
下标的标识分别为：0,1

当size为4时，掩码为3，二进制表示为11，掩码位两位：
那么原本的下标0,1，调整掩码位后为00 , 01
调整size1 = size0*2后的，原本的idx，分别产生idx与idx+size0两个下标，二进制表示则为下标二进制表示的掩码位的高位（最右的0）置1，如：
00， 高位的0置1，成10，值即为2；
01， 高位的0置1，成11，值即为3.
输出：00,10，01,11

当size为8时，掩码为7，二进制表示为111，掩码位三位：
原本下标为：00,10，01,11，调整掩码位后为000 , 010，001，011
同样掩码位最高位置1：
000 高位的0置1，成100，值即为4；
010 高位的0置1，成110，值即为6
001 高位的0置1，成101，值即为5；
011 高位的0置1，成111，值即为7；
此时的遍历顺序则为0,4，2,6，1,5，3,7

从0到4，从2到6，从1到5，从3到7是比较容易理解的，但是如果从4到2，从6到1呢：从上面的顺序可以看出，在旧空间同余的key,在新空间表现为低位槽，高位槽交替，也就说说如何从高位槽，遍历到下一个低位槽：
可以看出，下一个低位槽， 其实就是上一个低位槽在旧空间时的高位槽，比如长度为8时，低位槽为0（000），高位槽为4(100)，那么4的下一个低位槽2(010)，其实是长度为4时，低位槽0的高位槽。也就是说，要从高位槽遍历到下一个低位槽，就要将当前掩码位的最高位置位0，然后将次高位置位1，意思就是找在扩容前的低位槽2的高位槽，如：高位槽100，则变成010这个低位槽，而这个低位槽则是掩码只有两位时，即是扩容前的低位槽00 的高位槽。
如果本身低位就是2（010），高位槽是6（110），当6掩码位最高位置0后的010在旧空间也是高位槽那么再找下一个低位槽，就要最高位次高位都置0，次次高位置1即为001，以此类推。

也就是说，对于数a, 掩码位的1，表示以这个位作为掩码位最高位时，这个数都是高位槽
如：7(0000_0111) 掩码位111，最高位的1表示掩码位是三个位（size=8）时，该数是高位槽，次高位的1，表示掩码位是两个位（size=4）时，该数是高位槽，次次高位的1，表示掩码位是两个位（size=2）时，该数是高位槽

至此，也只是理论上，实现了调整遍历顺序，达到减少重复遍历的效果，但是怎么用位运算实现上面的理论呢，Redis的dictScan方法中使用了一种逆序运算的方法：

1、将下标逆序，从大端编码变成小端编码，如001，转换成100；
2、逆序后+1,100加1后为101
3、再逆序回来，变回大端编码，转换为101，此时的值就是下一个需要遍历的下标

dictScan的这个算法，实现了给掩码位的最高位置1，但是，神奇的事也发生了，使用同样的方式，竟然可以继续遍历到下一个扩容前非同余的下标。如：

101逆序后仍为101-》逆序后+1，值为110-》110再逆序回来，成011

前面这一大段的内容，就是描述下面这三行代码的逻辑

v = rev(v);
v++;
v = rev(v);

当然实际计算机位运算中，没法直接就知道只运算掩码覆盖的这几位，那么这三行代码前面那句v |= ~m0;就是通过游标与掩码的反码做或运算，标识需要运算的掩码覆盖的位，比如：

size为4，掩码为3，二进制0000 0011，游标为1，二进制0000 0001
v|= ~m0,即为0000 0001 | 1111 1100，得到v = 1111 1101
逆序后为 v=1011 1111
逆序后+1为 v = 1100 0000
再次逆序 v = 0000 0011,值为3，遍历1之后的下一个游标为3.

二进制的运算就是这样总是充满意想不到的神奇。