从力的角度再次比较9-2分布和8-3分布

news/2024/11/24 5:22:10/

( A, B )---1*30*2---( 1, 0 )( 0, 1 )

让网络的输入只有1个节点，AB各由11张二值化的图片组成，让A中有3个0，8个1.B中全是0，排列组合A的所有可能，统计迭代次数的顺序。在前面实验中得到了8-3分布的数据

A-B

迭代次数

标准差

11

 "00011111111"

3+f1

20470.21

0

0

8

3.771

11

 "01001111111"

3+f2

21099.48

1

0

7

3.091

11

 "00101111111"

3+f3

21759.81

0

1

7

3.091

11

 "01100111111"

3+f4

21810.68

2

0

6

2.494

11

 "01110011111"

3+f5

22313.81

3

0

5

2.055

11

 "01010111111"

3+f6

22402.91

1

1

6

2.357

11

 "01111001111"

3+f7

22920.43

4

0

4

1.886

11

 "00110111111"

3+f8

22920.3

0

2

6

2.494

11

 "01101011111"

3+f9

23066.35

2

1

5

1.7

11

 "00111011111"

3+f10

23183.93

0

3

5

2.055

11

 "01110101111"

3+f11

23570.92

3

1

4

1.247

11

 "01011011111"

3+f12

23729.11

1

2

5

1.7

11

 "01011101111"

3+f13

24086.94

1

3

4

1.247

11

 "01101101111"

3+f14

24342.91

2

2

4

0.943

11

 "01110111011"

3+f15

24833.37

3

3

2

0.471

也得到了9-2分布的数据

A-B

迭代次数

标准差

11

0*0*1*1*1*1*1*1*1*1*1

2+g1

18792.34

0

9

4.5

11

0*1*0*1*1*1*1*1*1*1*1

2+g2

19501.1

1

8

3.5

11

0*1*1*0*1*1*1*1*1*1*1

2+g3

19969.63

2

7

2.5

11

0*1*1*1*0*1*1*1*1*1*1

2+g4

20556.24

3

6

1.5

11

0*1*1*1*1*0*1*1*1*1*1

2+g5

21103.48

4

5

0.5

收敛误差7e-4，每组收敛199次。统计平均值

这次用列排斥力的方法把这两组数据放在一起去比较，观察迭代次数的大小变化顺序。

 

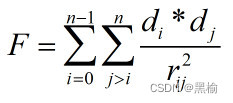
如计算3+f2的"01001111111"

0

1

0

0

1

1

1

1

1

1

1

1

2

3

4

5

6

7

8

9

10

11

1

2

0.11

0.06

0.04

0.03

0.02

0.02

0.01

3

4

5

1

0.25

0.11

0.06

0.04

0.03

6

1

0.25

0.11

0.06

0.04

7

1

0.25

0.11

0.06

8

1

0.25

0.11

9

1

0.25

10

1

11

F=8.2794

其余各组数据为

A-B

迭代次数

F

标准差

11

0*0*1*1*1*1*1*1*1*1*1

2+g1

18792.34

11.02894

0

9

4.5

11

0*1*0*1*1*1*1*1*1*1*1

2+g2

19501.1

10.04129

1

8

3.5

11

0*1*1*0*1*1*1*1*1*1*1

2+g3

19969.63

9.806912

2

7

2.5

11

 "00011111111"

3+f1

20470.21

9.501519

0

0

8

3.77124

11

0*1*1*1*0*1*1*1*1*1*1

2+g4

20556.24

9.716209

3

6

1.5

11

 "01001111111"

3+f2

21099.48

8.27949

1

0

7

3.09121

11

0*1*1*1*1*0*1*1*1*1*1

2+g5

21103.48

9.681487

4

5

0.5

11

 "00101111111"

3+f3

21759.81

8.517144

0

1

7

3.09121

11

 "01100111111"

3+f4

21810.68

7.954412

2

0

6

2.49444

11

 "01110011111"

3+f5

22313.81

7.828987

3

0

5

2.0548

11

 "01010111111"

3+f6

22402.91

7.438787

1

1

6

2.35702

11

 "00110111111"

3+f8

22920.3

8.287552

0

2

6

2.49444

11

 "01111001111"

3+f7

22920.43

7.794265

4

0

4

1.88562

11

 "01101011111"

3+f9

23066.35

7.16969

2

1

5

1.69967

11

 "00111011111"

3+f10

23183.93

8.204219

0

3

5

2.0548

11

 "01110101111"

3+f11

23570.92

7.078987

3

1

4

1.24722

11

 "01011011111"

3+f12

23729.11

7.265176

1

2

5

1.69967

11

 "01011101111"

3+f13

24086.94

7.216565

1

3

4

1.24722

11

 "01101101111"

3+f14

24342.91

7.030801

2

2

4

0.94281

11

 "01110111011"

3+f15

24833.37

7.016912

3

3

2

0.4714

比较标准差曲线

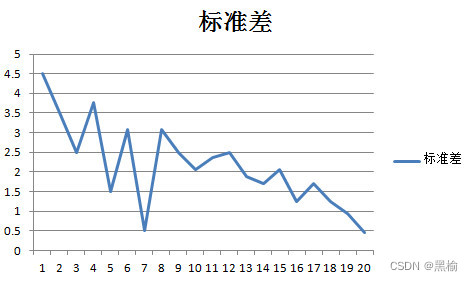
数值波动很大，再比较列排斥力曲线

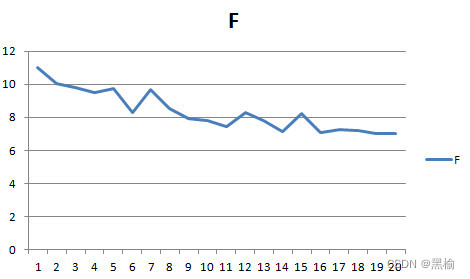
数据要平滑很多。力与迭代次数的反比关系清晰。


http://www.ppmy.cn/news/59542.html

相关文章

五一欢乐赛!题解

五一欢乐赛!题解

前言 五一欢乐赛有点一言难尽, 这次本来想的给大火减减压放了很多区域赛和省赛的签到题(还有一些是写过的题), 没想到打的并不是很理想, 还用了分数值想减少一些差距, 结果看起来好像让差距更大了, 尴尬 虽然不是很想打击各位, 但是省赛/区域赛的签到题都写成这样, 明年就等着…
阅读更多...
分享5款轻量级的Win10神器，错过你会后悔的

分享5款轻量级的Win10神器，错过你会后悔的

今天我要为大家推荐五款小众而且小体积的WIN10小工具，它们可以让你的电脑使用更加方便和高效，而且不占用太多的空间和资源，非常适合轻量级的办公和娱乐。 1.窗口管理工具——TileIconifier TileIconifier可以将窗口最小化到托盘区域,从而更…
阅读更多...
perf record对C++程序耗时进行分析

perf record对C++程序耗时进行分析

本节将介绍如何使用perf工具的perf record对C代码进行性能分析，一切操作都是在ubuntu 20下进行。 perf工具安装 由于perf工具和内核版本有关，因此直接安装容易出错，建议直接通过如下指令安装： sudo apt-get install linux-tool…
阅读更多...
JavaWeb ( 四 ) JavaEE

JavaWeb ( 四 ) JavaEE

2.JavaEE 2.1.Java版本 J2SE : 适用于桌面系统的Java 2平台标准版（Java 2 Platform Standard Edition，J2SE） J2EE : 适用于创建服务器应用程序和服务的Java 2平台企业版（Java 2 Platform Enterprise Edition，J2EE&a…
阅读更多...
记一次我的漏洞挖掘实战——某公司的SQL注入漏洞

记一次我的漏洞挖掘实战——某公司的SQL注入漏洞

目录 一、前言 二、挖掘过程 1.谷歌语法随机搜索 2.进入网站 3.注入点检测 3.SQLMAP爆破 （1）爆库 （2）爆表 （3）爆字段 三、总结 一、前言 我是在漏洞盒子上提交的漏洞，上面有一个项目叫…
阅读更多...
redis服务搭建，C++实现redis客户端，redis远程可视化工具

redis服务搭建，C++实现redis客户端，redis远程可视化工具

目录 redis简介redis服务搭建redis常用命令C实现redis客户端redis远程可视化工具:Another Redis DeskTop Manager redis简介 官方网址：https://redis.io/ 开源地址：https://github.com/redis 中文文档：http://www.redis.cn/documentation.ht…
阅读更多...
Java 中的线程是什么，如何创建和管理线程-下（十三）

Java 中的线程是什么，如何创建和管理线程-下（十三）

书接上文 CompletableFuture CompletableFuture 是 Java 8 中新增的类，提供了更为强大的异步编程支持。它可以将多个异步任务组合成一个整体，并且可以处理异常情况。 例如，可以使用 CompletableFuture 来实现异步任务的串行执行&#xff1…
阅读更多...
行人重识别数据集Person Re-Identification Datasets(全)

行人重识别数据集Person Re-Identification Datasets(全)

DatasetRelease time# identities# cameras# imagesLabel methodCrop sizeMulti-shotTracking sequencesFull frames availabilityVIPeR200763221264Hand128X48ETH1,2,3200785, 35, 2818580HandVary✔✔✔QMUL iLIDS20091192476HandVary✔GRID2009102581275HandVaryCAVIAR4ReID…
阅读更多...
最新文章

Copyright @ 2022~2023