3. 课程表 Course Schedule III

这里有 n 门不同的在线课程，按从 1 到 n 编号。给你一个数组 courses ，其中 courses[i] = [durationi, lastDayi] 表示第 i 门课将会持续上 durationi 天课，并且必须在不晚于 lastDayi 的时候完成。

你的学期从第 1 天开始。且不能同时修读两门及两门以上的课程。

返回你最多可以修读的课程数目。

示例 1：

输入：courses = [[100, 200], [200, 1300], [1000, 1250], [2000, 3200]]
输出：3
解释：
这里一共有 4 门课程，但是你最多可以修 3 门：
首先，修第 1 门课，耗费 100 天，在第 100 天完成，在第 101 天开始下门课。
第二，修第 3 门课，耗费 1000 天，在第 1100 天完成，在第 1101 天开始下门课程。
第三，修第 2 门课，耗时 200 天，在第 1300 天完成。
第 4 门课现在不能修，因为将会在第 3300 天完成它，这已经超出了关闭日期。

示例 2：

输入：courses = [[1,2]]
输出：1

示例 3：

输入：courses = [[3,2],[4,3]]
输出：0

提示:

1 <= courses.length <= 10^4
1 <= durationi, lastDayi <= 10^4

代码： 贪心算法

package mainimport ("fmt""sort"
)func scheduleCourse(courses [][]int) int {// 按照截止日期升序排序sort.Slice(courses, func(i, j int) bool {return courses[i][1] < courses[j][1]})time := 0selected := make([][]int, 0)for _, c := range courses {if time+c[0] <= c[1] {selected = append(selected, []int{c[0], c[1]})time += c[0]sort.Slice(selected, func(i, j int) bool {return selected[i][0] > selected[j][0]})} else if len(selected) > 0 && c[0] < selected[0][0] {time += c[0] - selected[0][0]selected[0] = []int{c[0], c[1]}sort.Slice(selected, func(i, j int) bool {return selected[i][0] > selected[j][0]})}}return len(selected)
}func main() {courses := [][]int{{100, 200}, {200, 1300}, {1000, 1250}, {2000, 3200}}fmt.Println(scheduleCourse(courses))courses = [][]int{{1, 2}}fmt.Println(scheduleCourse(courses))
}

输出：

3
1

4. 课程表 Course Schedule IV

你总共需要上 numCourses 门课，课程编号依次为 0 到 numCourses-1 。你会得到一个数组 prerequisite ，其中 prerequisites[i] = [ai, bi] 表示如果你想选 bi 课程，你必须先选 ai 课程。

有的课会有直接的先修课程，比如如果想上课程 1 ，你必须先上课程 0 ，那么会以 [0,1] 数对的形式给出先修课程数对。

先决条件也可以是间接的。如果课程 a 是课程 b 的先决条件，课程 b 是课程 c 的先决条件，那么课程 a 就是课程 c 的先决条件。

你也得到一个数组 queries ，其中 queries[j] = [uj, vj]。对于第 j 个查询，您应该回答课程 uj 是否是课程 vj 的先决条件。

返回一个布尔数组 answer ，其中 answer[j] 是第 j 个查询的答案。

示例 1：

输入：numCourses = 2, prerequisites = [[1,0]], queries = [[0,1],[1,0]]
输出：[false,true]
解释：课程 0 不是课程 1 的先修课程，但课程 1 是课程 0 的先修课程。

示例 2：

输入：numCourses = 2, prerequisites = [], queries = [[1,0],[0,1]]
输出：[false,false]
解释：没有先修课程对，所以每门课程之间是独立的。

示例 3：

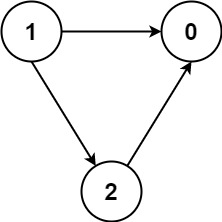
输入：numCourses = 3, prerequisites = [[1,2],[1,0],[2,0]], queries = [[1,0],[1,2]]
输出：[true,true]

提示：

2 <= numCourses <= 100
0 <= prerequisites.length <= (numCourses * (numCourses - 1) / 2)
prerequisites[i].length == 2
0 <= ai, bi <= n - 1
ai != bi
每一对 [ai, bi] 都不同
先修课程图中没有环。
0 <= ui, vi <= n - 1
ui != vi

代码：

package mainimport "fmt"func checkIfPrerequisite(numCourses int, prerequisites [][]int, queries [][]int) []bool {// 构建课程图n := numCoursesgraph := make([][]int, n)inDegree := make([]int, n)for _, p := range prerequisites {ai, bi := p[0], p[1]graph[ai] = append(graph[ai], bi)inDegree[bi]++}// BFS 拓扑排序queue := make([]int, 0)for i := 0; i < n; i++ {if inDegree[i] == 0 {queue = append(queue, i)}}successors := make([][]int, n)for len(queue) > 0 {node := queue[0]queue = queue[1:]for _, neighbor := range graph[node] {inDegree[neighbor]--if inDegree[neighbor] == 0 {queue = append(queue, neighbor)}// 记录 successor 节点successors[node] = append(successors[node], neighbor)for _, s := range successors[neighbor] {successors[node] = append(successors[node], s)}}}// 对每个查询进行检查result := make([]bool, len(queries))for i, q := range queries {ui, vi := q[0], q[1]for _, s := range successors[ui] {if s == vi {result[i] = truebreak}}}return result
}func main() {numCourses := 2prerequisites := [][]int{{1, 0}}queries := [][]int{{0, 1}, {1, 0}}fmt.Println(checkIfPrerequisite(numCourses, prerequisites, queries))prerequisites = [][]int{}queries = [][]int{{1, 0}, {0, 1}}fmt.Println(checkIfPrerequisite(numCourses, prerequisites, queries))
}

输出：

[false true]
[false false]