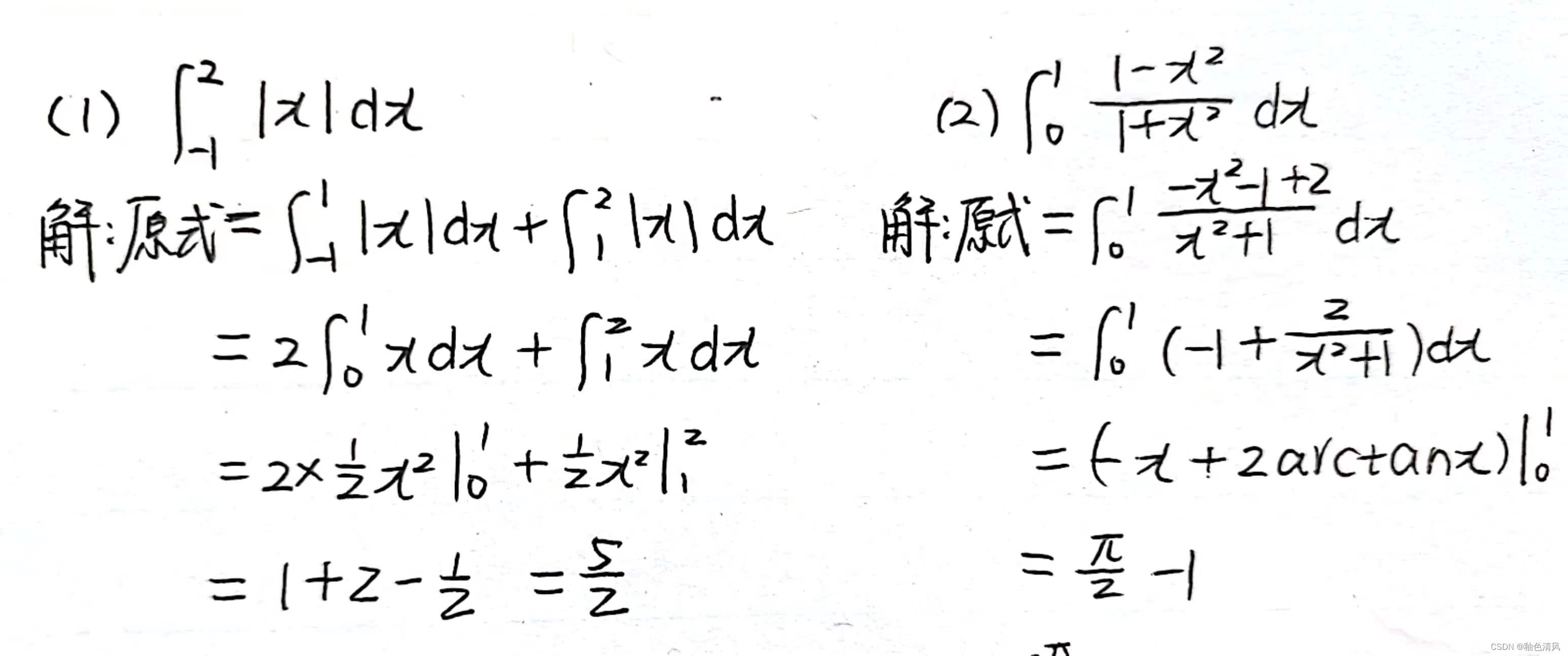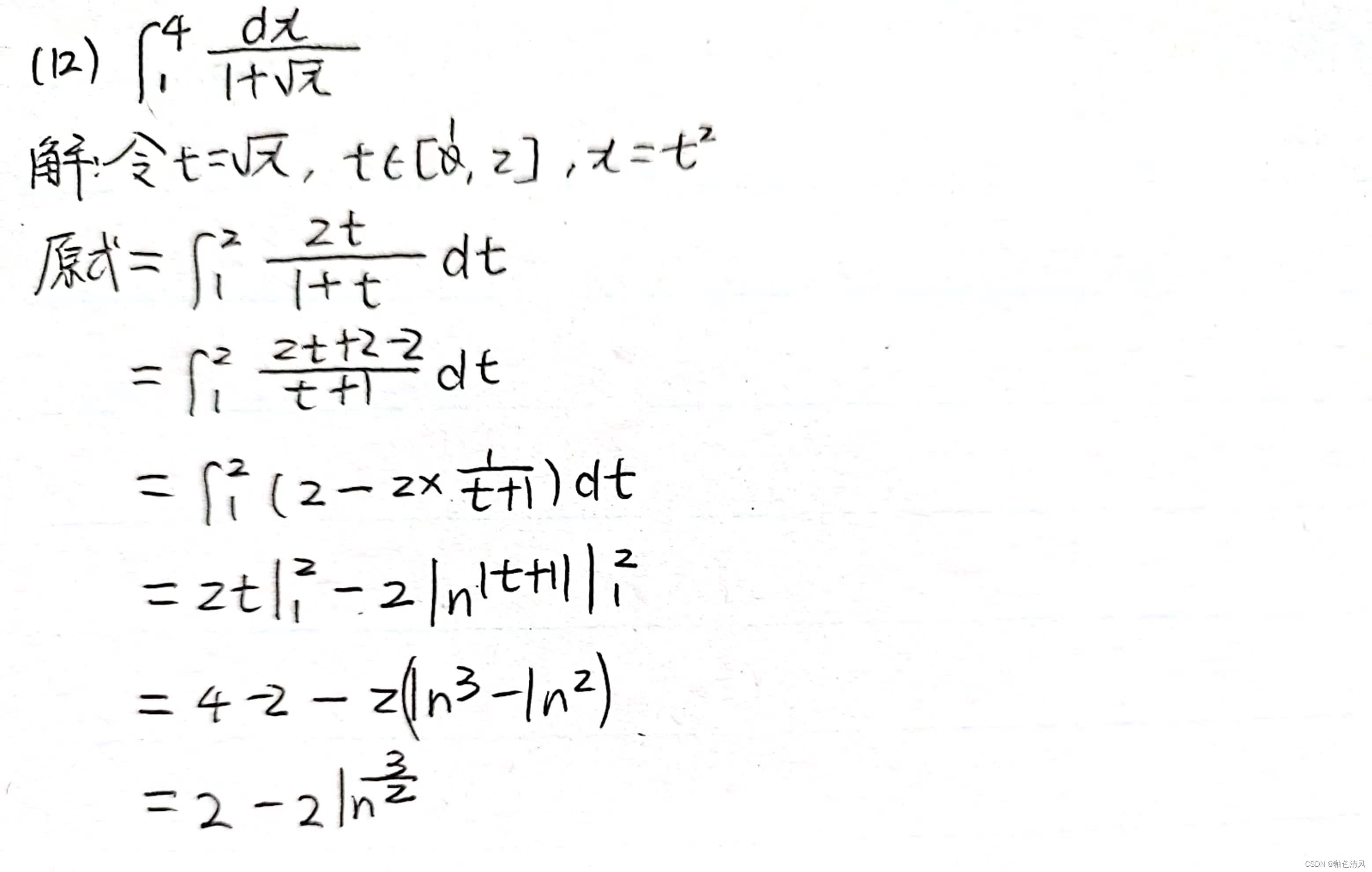定积分计算
- 前言
- 定积分的常规计算技巧—牛顿-莱布尼茨公式
- 定积分的几何意义
- 利用奇偶性简化计算
- 利用周期性平移和缩小积分区间
- 利用Wallis公式
- 利用一个常见的积分公式
- 定积分计算练习题
前言
定积分的计算依赖于不定积分的计算,其基本方法是利用牛顿莱布尼茨公式,即算出f(x)的原函数F(x)之后,在区间[a,b]的端点上作差即可。
但是,一个函数在区间[a,b]上可积与在区间[a,b]上存在原函数是两个截然不同的概念。
有些函数f(x)再区间[a,b]可积,但是却不存在原函数。
有些函数f(x)再区间[a,b]上存在原函数F(x),但是却不可积。
所以,利用N-L公式计算积分的前提是—函数f(x)在区间[a,b]上不仅存在原函数,而且还可积。
显然,对于那些可积却又不存在原函数的函数f(x),在求其定积分时,无法使用N-L公式。并且即便一个函数f(x)既存在原函数,也可积,但是其原函数很有可能不是初等函数。
基于以上种种原因,我们同时也需要找到一些其他的方法来计算定积分的值。
常用的技巧有如下几个:
利用定积分的几何意义
利用奇偶性化简计算
利用周期性平移和缩小积分区间
利用区间再现公式简化计算
利用Wallis公式
利用一个常见的积分公式
这次我们主要利用牛顿-莱布尼茨公式,利用定积分的几何意义,利用周期性平移和缩小积分区间,利用wallis公式来学习定积分的计算。🤗🤗
最主要的定积分的计算当然还是牛顿-莱布尼茨公式啦,所以在本篇的最后,配有一些简单的练习题,不妨简单做一下练练手吧!🥳🥳
定积分的常规计算技巧—牛顿-莱布尼茨公式
例题1


例题2

思想

首先,我们先根据这个思想解一道题目,再返回去看看例题2。
引例


注
在本题中,换元之后,最好不要将dx解出来,而应该直接分部。否则被积函数次数太高不好做!
好接下来,我们接着看上面的例题2。


这道题目包含很多平时处理的技巧很不错👻
例题3

这道题目和上一题有一些类似,但好像更加吓人,因为它是根号里面又有个根号。
这时候要怎么处理呢?首先,我们所谓的步骤都是为了我们最终的目的而服务的。我们希望我们的式子中不会出现根号,所以这么想,我们直接就令外面这个大根号为t,那么被积函数会成为arcrant就看起来好很多了。

这一题,需要注意的是同上一题一样,反解出来x之后,放在d后面,千万不要进行求导了,这样会把题目放复杂很多的。
以上几道题,本质上其实就是不定积分的计算,只是多了最后一步“代入上下限”而已。
例题4

先来看错误的解法,你有没有进坑呢?

但是显而易见被积函数在其被积区间恒大于0,那么其积分就一定大于0,所以上面的解法就一定是错的。
由定理:

若有原函数,原函数求导得到f,那么原函数F一定连续。
而反过来看上面那道题,得到了原函数,但F在 π 2 π 2 \frac{\pi}{2}\frac{\pi}{2} 2π2π均没有定义,不连续。(实际上在第一个等号处就很不严谨了,同时除以 c o s 2 x cos^2x cos2x,而在区间[0, 2 π 2\pi 2π]上cosx有为0的点)
而在积分区间内部出现无定义点,是不能使用牛顿莱布尼茨公式的。
那如何解决这个问题呢?将积分区间从无定义点处拆开,拆分成若干个小积分之和。对于每一个小积分而言,无定义点都是积分区间的端点,而不在积分区间的内部。
此时,对每个小积分使用推广的牛顿莱布尼兹公式,即可正确算出积分值。

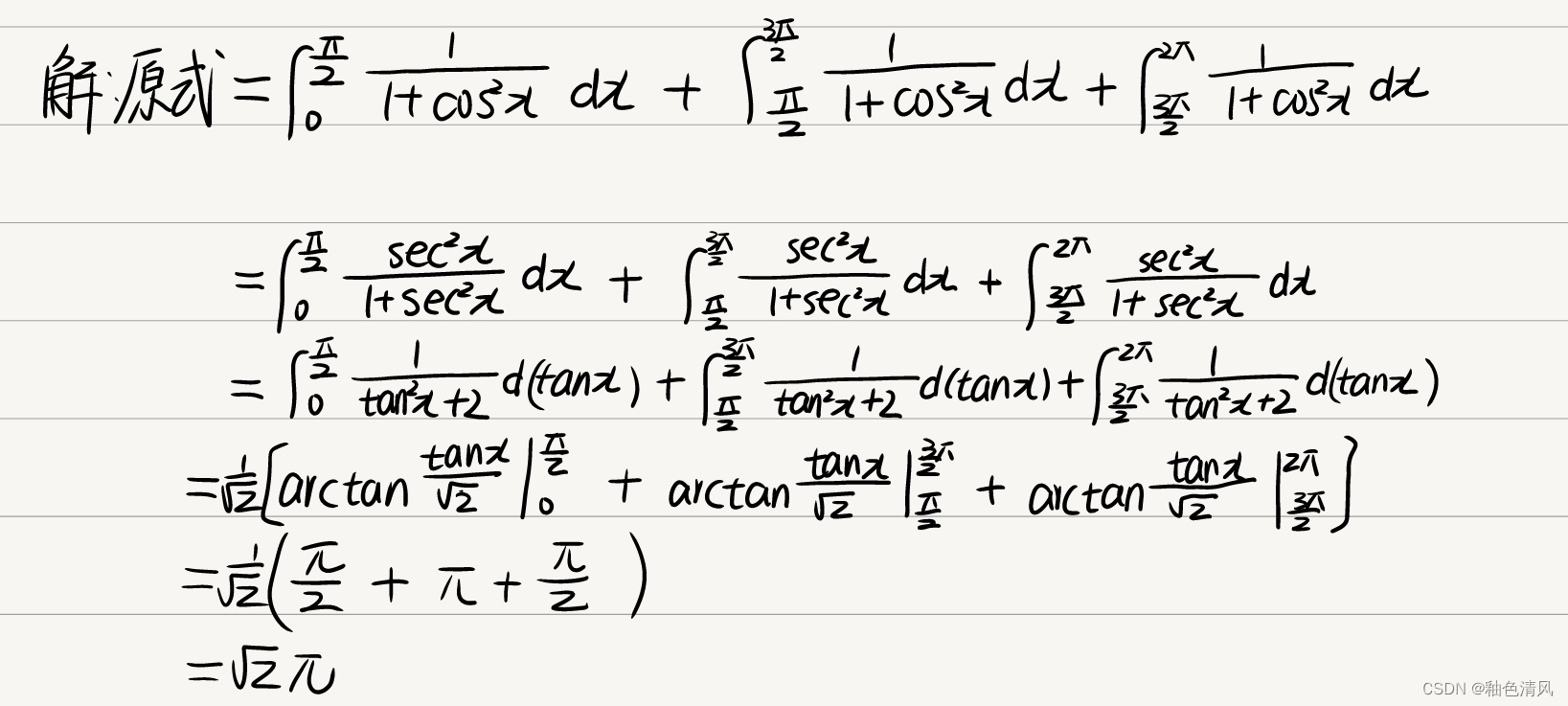
但是,这样做同样的计算写了好几遍有些繁琐。
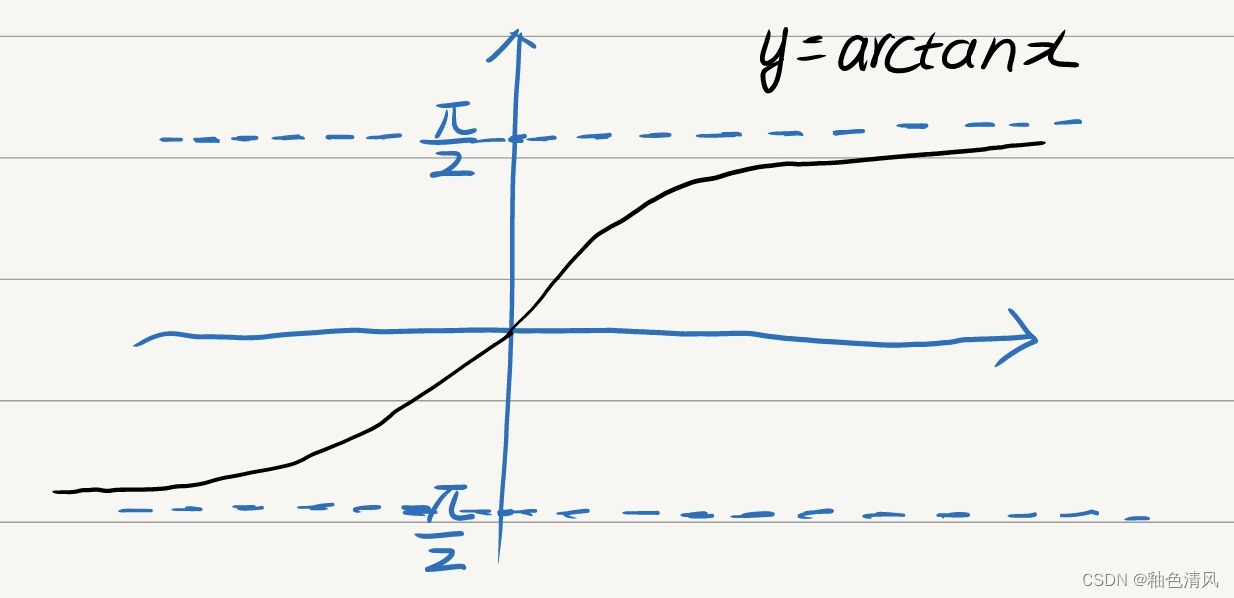
所以,我们可以利用周期性和对称性,提前将无定义点从积分区间内部移出。

定积分的几何意义
利用定积分的几何意义来计算定积分的值
例题1

若不用几何意义,利用换元法进行计算。

利用奇偶性简化计算
例题

利用周期性平移和缩小积分区间

例题1

例题2

利用Wallis公式

推广:

利用一个常见的积分公式
定积分计算练习题