1.frame overviews

SVO的整体框架如链接，可以看到整个SVO的结构是由两个线程构成的，第一个线程有三个主要的操作，a. Sparse Model-based Image Alignment; b. Feature Alignment; c. Pose&Structure Refinement。第二个线程主要是map的过程，一旦有一帧被定义为keyframe，就提取其中的feature，并初始化深度滤波器，如果不是keyframe，则一直更新深度滤波器，如果某个feature的深度收敛了，则生成3D点放入Map中作为landmark。

2. Motion Estimate Thread

该线程中主要求解当前帧的位姿(Sparse Model-based Image Alignment; Feature Alignment)和local BA(Pose&Structure Refinement). svo 方法中motion estimation的步骤可以简单概括如下:

对稀疏的特征块使用direct method 配准，获取相机位姿；
通过获取的位姿预测参考帧中的特征块在当前帧中的位置，由于深度估计的不准导致获取的位姿也存在偏差，从而使得预测的特征块位置不准。由于预测的特征块位置和真实位置很近，所以可以使用牛顿迭代法对这个特征块的预测位置进行优化。
特征块的预测位置得到优化，说明之前使用直接法预测的有问题。利用这个优化后的特征块预测位置，再次使用直接法，对相机位姿(pose)以及特征点位置（structure）进行优化

2.1 Sparse Model-based Image Alignment 基于稀疏点亮度的位姿预估

该部分类似于光流，不过求解的不是对应关系，而是相对位姿。

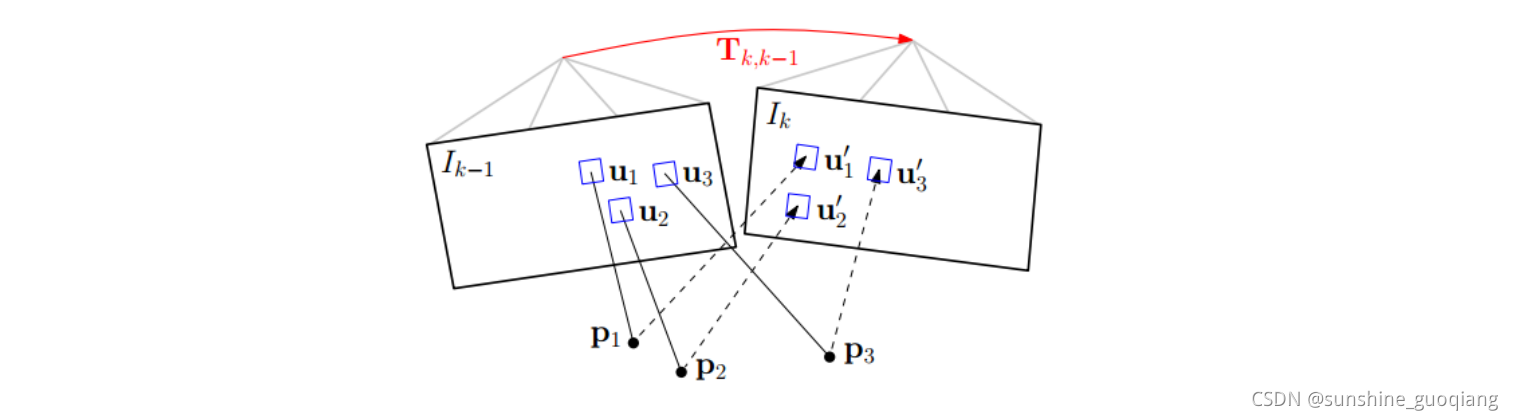
直接法具体过程如下：
  step1. 准备工作。假设相邻帧之间的位姿$T_{k,k-1}$已知，一般初始化为上一相邻时刻的位姿或者假设为单位矩阵。通过之前多帧之间的特征检测以及深度估计，我们已经知道第k-1帧中特征点位置以及它们的深度。
  step2. 重投影。知道$I_{k-1}$中的某个特征在图像平面的位置(u,v)，以及它的深度d，能够将该特征投影到三维空间$p_{k-1}$，该三维空间的坐标系是定义在$I_{k-1}$摄像机坐标系的。所以，我们要将它投影到当前帧$I_k$中，需要位姿转换$T_{k,k-1}$，得到该点在当前帧坐标系中的三维坐标$p_k$。最后通过摄像机内参数，投影到$I_k$的图像平面$(u\prime ,v\prime )$，完成重投影。
  step3. 迭代优化更新位姿 。按理来说对于空间中同一个点，被极短时间内的相邻两帧拍到，它的亮度值应该没啥变化。但由于位姿是假设的一个值，所以重投影的点不准确，导致投影前后的亮度值是不相等的。不断优化位姿使得这个残差最小，就能得到优化后的位姿$T_{k,k-1}$。
  将上述过程公式化如下：通过不断优化位姿$T_{k,k-1}$最小化残差损失函数。其优化函数为:
$$T_{k-1}^k=argmin{\iint }_{\Re }\rho [\delta I(T,u)]du$$
其中:

1. $\rho [\ast ]=0.5\Vert \ast {\Vert }^2$，可见整个过程是一个最小二乘法的问题；

2. $\delta I(T,u)=I_k(\pi (T\ast {\pi }^{-1}(u,du)))-Ik-1(u)$，这个残差对比的是图像位置上的像素值的灰度，其中u ∈ ℜ ,ℜ表示即可以在k-1帧图像上看到，又可以通过投影在k帧上看到

3. 对于比对灰度值的算法来说，一般都会用一个patch size中的全部像素的灰度进行对比，因此下面的公式中都不仅仅使用一点像素，而是使用多点像素进行求解的，但是在这个过程中，作者为了提高计算的速度，并没有进行patch的投影，算是以量取胜吧

NOTE:公式中 ${\pi }^{-1}(u,du)$ 为根据图像位置和深度逆投影到三维空间，第二步 $T\ast {\pi }^{-1}(u,du)$ 将三维坐标点旋转平移到当前帧坐标系下，第三步 $\pi (T\ast {\pi }^{-1}(u,du))$ 再将三维坐标点投影回当前帧图像坐标。当然在优化过程中，残差的计算方式不止这一种形式：有前向(forwards)，逆向(inverse)之分，并且还有叠加式(additive)和构造式(compositional)之分。这方面可以读读光流法方面的论文，Baker的大作《Lucas-Kanade 20 Years On: A Unifying Framework》。选择的方式不同，在迭代优化过程中计算雅克比矩阵的时候就有差别，一般为了减小计算量，都采用的是inverse compositional algorithm。

优化目标函数：

把上述的notation带入到优化函数中就可以得到
$$T_{k-1}^k=argmin\sum _{i\in \Re }1/2\Vert \delta I(T_{k-1}^k,u_i){\Vert }^2$$
其中雅克比矩阵为图像残差对李代数的求导，可以通过链式求导得到：
$$J=\frac{\partial \delta I(\xi ,u_i)}{\partial \xi }=\frac{\partial I_{k-1}(a)}{\partial a}{|}_{a=u_i}.\frac{\partial \pi (b)}{\partial b}{|}_{b=p_i}.\frac{\partial T(\xi )}{\partial \xi }{|}_{\xi =0}.p_i=\frac{\partial I}{\partial u}.\frac{\partial u}{\partial b}.\frac{\partial b}{\partial \xi }$$
对于上一帧的每一个特征点，都进行这样的计算， 在自己本来的层数上， 取那个特征点左上角的 4x4 图块。如果特征点映射回原来的层数时，坐标不是整数，就进行插值，其实，本来提取特征点的时候，在这一层特征点坐标就应该是整数。把图块往这一帧的图像上的对应的层数投影，然后计算雅克比和残差。 计算残差时， 因为投影的位置并不刚好是整数的像素，所以会在投影点附近插值，获取与投影图块对应的图块。最后，得到一个巨大的雅克比矩阵，以及残差矩阵。但是为了节省存储空间，提前就转换成了 H 矩阵 $ H =J *J ^ T$ 。

上面的非线性最小化二乘问题，可以用高斯牛顿迭代法求解，位姿的迭代增量ξ(李代数)可以通过下述方程计算：
$$\begin{gathered} J^{T}J\xi =-J^T\delta I(0) \\ H\xi =-J^T\delta I(0) \\ \xi =-H^{-1}{J}^T\delta I(0) \end{gathered}$$
然后，得到 $T(\xi )$ ，逆矩阵得到 $T(\psi )$ ，再更新出 $T_{k,k-1}$ 。然后，在新的位置上，再从像素点坐标，投影出新的点 $p_{k-1}$。每一层迭代 30 次。 因为这种 inverse-compositional 方法，用这种近似的思想，雅克比就可以不用再重新计算了。（因为重新投影出新的 p 点的位置， 这个过程没有在残差公式里面表现出来。） 这样子逐层下去，重复之前的步骤。

对于每一个图块的每一个像素，它的雅克比计算如下。
$\frac{\partial I}{\partial u}$， 是这个像素插值点在图像上的梯度，就是水平右边的像素点减去水平左边的像素点，竖直下边的像素点减去竖直上边的像素点。如下图所示。

$\frac{\partial u}{\partial b}$算的是投影雅克比
$$u=\pi (b)=K\left[\begin{array}{c}{b}_x/b_z\\ b_y/b_z\\ b_z/b_z\end{array}\right]=\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]\ast \left[\begin{array}{c}{b}_x/b_z\\ b_y/b_z\\ 1\end{array}\right]=\left[\begin{array}{c}{f}_x{b}_x/b_z+u_0\\ f_y{b}_y/b_z+v_0\\ 1\end{array}\right]$$
$$\frac{\partial u}{\partial b}=\left[\begin{array}{ccc}{f}_x/b_z& 0& -f_x.b_x/b_z^2\\ 0& f_y/b_z& -f_y.b_y/b_z^2\end{array}\right]$$

$$\frac{\partial b}{\partial \xi }=\frac{\partial T(\xi )p}{\partial \xi }=[I-p^{\wedge }]=\frac{\partial (\delta {\varphi }^{\wedge }+\delta \rho )}{\partial [\delta \rho \delta \varphi ]}$$
$$=\left[\begin{array}{cccccc}1& 0& 0& 0& p_z& -p_y\\ 0& 1& 0& -p_z& 0& p_x\\ 0& 0& 1& p_y& -p_x& 0\end{array}\right]$$
为了方便计算，虽然 $b=T(\xi )p$ ，但因为$T(\xi )$ 是一个很小的扰动，所以可以认为 $b=T(\xi )p$,

$\frac{\partial u}{\partial b}=\frac{\partial u}{\partial T(\xi )p}\approx \frac{\partial u}{\partial p}$

所以，后两项就可以相乘，统一用 p 来表示了。 可以认为$ f =f_x=f_y$ 。

因此，

$$\frac{\partial u}{\partial b}=\frac{\partial b}{\partial \xi }=\left[\begin{array}{ccc}{f}_x/b_z& 0& -f_x.b_x/b_z^2\\ 0& f_y/b_z& -f_y.b_y/b_z^2\end{array}\right]\ast \left[\begin{array}{cccccc}1& 0& 0& 0& p_z& -p_y\\ 0& 1& 0& -p_z& 0& p_x\\ 0& 0& 1& p_y& -p_x& 0\end{array}\right]$$
$$=\left[\begin{array}{cccccc}{f}_x/p_z& 0& -f_x/p_z^2& -f_x{p}_x{p}_y/p_z^2& f_x+f_x{p}_x^2/p_z^2& -f_x{p}_y/p_z\\ 0& f_y/p_z& -f_y/p_z^2& -f_y-f_y{p}_y^2/p_z^2& -f_y{p}_y{p}_y/p_z^2& f_y{p}_x/p_z\end{array}\right]$$

$$=[].f(f_x、f_y)$$
对于每一个特征点，根据像素位置算出$\frac{\partial I}{\partial u}$，再根据反投影出来的空间点位置 p 算出上式的左边项，根据特征点所在的层数算出 f 。然后，相乘，就得到了一行雅克比矩阵。 再根据 $H=J J ^ T $，$J^TJξ =-J^T \delta I(0)$加到 H 矩阵和残差矩阵上。

最后，在优化出$\xi$ 后，更新如下，
$$T_{k,k-1}=T_{k,k-1}{T}_{k-1,k-1}=T_{k,k-1}{T}_{\psi }=T_{k,k-1}T(\xi {)}^{-1}$$
注释：但是在程序里面，直接就是$T_{k,k-1}=T_{k,k-1}T(\xi )$ 。可能是为了加快计算，认为$T(\xi {)}^{-1}\approx T_{k,k-1}$ 。 在 sparse_align.cpp 的 307行

T_curnew_from_ref = T_curold_from_ref * SE3::exp(-x_); 这个地方， 为什么不是 T_curnew_from_ref = T_curold_from_ref *(SE3::exp(x_)).inverse()**需要以后研究一下。

到这里，我们已经能够估计位姿了，但是这个位姿肯定不是完美的。导致重投影预测的特征点在中的位置并不和真正的吻合，也就是还会有残差的存在。如下图所示：

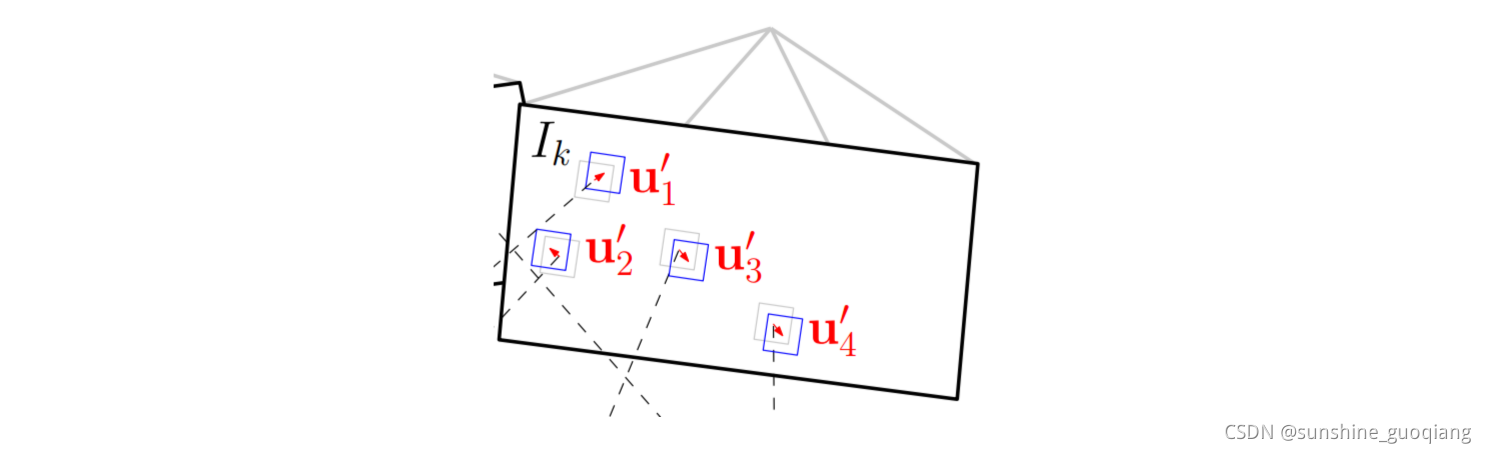
图中灰色的特征块为真实位置，蓝色特征块为预测位置。幸好，他们偏差不大，可以构造残差目标函数，和上面直接法类似，不过优化变量不再是相机位姿，而是像素的位置$(u\prime ,v\prime )$，通过迭代对特征块的预测位置进行优化。这就是svo中提到的Feature Alignment。

2.2 Relaxation Through Feature Alignment 基于图块的特征点匹配

通过第一步的帧间匹配能够得到当前帧相机的位姿，但是这种frame to frame估计位姿的方式不可避免的会带来累计误差从而导致漂移。所以，应该通过已经建立好的地图模型，来进一步约束当前帧的位姿。

地图模型通常来说保存的就是三维空间点，因为每一个Key frame通过深度估计能够得到特征点的三维坐标，这些三维坐标点通过特征点在Key Frame中进行保存。所以SVO地图上保存的是Key Frame 以及还未插入地图的KF中的已经收敛的3d点坐标（这些3d点坐标是在世界坐标系下的），也就是说地图map不需要自己管理所有的3d点，它只需要管理KF就行了。

那选取KF的标准是啥？KF中保存了哪些东西？

比如，当新的帧new frame和相邻KF的平移量超过场景深度平均值的12%时(比如四轴上升)，new frame就会被当做KF，它会被立即插入地图。同时，又在这个新的KF上检测新的特征点作为深度估计的seed，这些seed会不断融合新的new frame进行深度估计。

但是，如果有些seed点3d点位姿通过深度估计已经收敛了，怎么办？

map用一个point_candidates来保存这些尚未插入地图中的点。所以map这个数据结构中保存了两样东西，以前的KF的3d点以及新的尚未插入地图的KF中已经收敛的3d点。

通过地图我们保存了很多三维空间点，很明显，每一个new frame都是可能看到地图中的某些点的。由于new frame的位姿通过上一步的直接法已经计算出来了，按理来说这些被看到的地图上的点可以被投影到这个new frame中，即图中的蓝色方框块。上图中分析了，所有位姿误差导致这个方框块在new frame中肯定不是真正的特征块所处的位置。所以需要Feature Alignment来找到地图中特征块在new frame中应该出现的位置，根据这个位置误差为进一步的优化做准备。基于光度不变性假设，特征块在以前参考帧中的亮度应该和new frame中的亮度差不多。所以可以重新构造一个残差，对特征预测位置进行优化：
$$u_i^{\prime }=argmin\frac{1}{2}\Vert I_k(u_i^{\prime })-A_i{I}_r(u_i){\Vert }^2$$
注意这里的优化变量是像素位置，这过程就是光流法跟踪。并且注意，光度误差的前一部分是当前图像中的亮度值，后一部分不是 $I_{k-1}$而是 $i_r$，即它是根据投影的3d点追溯到的这个3d点所在的key frame中的像素值，而不是相邻帧。由于是特征块对比并且3d点所在的KF可能离当前帧new frame比较远，所以光度误差和前面不一样的是还加了一个仿射变换，需要对KF帧中的特征块进行旋转拉伸之类仿射变换后才能和当前帧的特征块对比。
  这时候的迭代量计算方程和之前是一样的，只不过雅克比矩阵变了，这里的雅克比矩阵很好计算：
KaTeX parse error: Undefined control sequence: \matrix at position 12: J= \left[ \̲m̲a̲t̲r̲i̲x̲{ \frac{\part…
就是图像横纵两个方向的梯度嘛。
  通过这一步我们能够得到优化后的特征点预测位置，它比之前通过相机位姿预测的位置更准，所以反过来，我们利用这个优化后的特征位置，能够进一步去优化相机位姿以及特征点的三维坐标。所以位姿估计的最后一步就是Pose and Structure Refinement。

2.3 Pose and Structure Refinement

在一开始的直接法匹配中，我们是使用的光度误差，这里由于优化后的特征位置和之前预测的特征位置存在差异，这个能用来构造新的优化目标函数。
$$T_{w,k}=argmin\frac{1}{2}\sum _i(\Vert u_i-\pi (T_{w,k}{,}_w{p}_i)\Vert {)}^2$$
这个部分就是一个BA，不过论文也说了，最后一步也会有一个local BA，修正位姿和3D点

上式中误差变成了像素重投影以后位置的差异（不是像素值的差异），优化变量还是相机位姿，雅克比矩阵大小为2×6(横纵坐标u，v分别对六个李代数变量求导)。这一步是就叫做motion-only Bundler Adjustment。同时根据根据这个误差定义，我们还能够对获取的三维点的坐标(x,y,z)进行优化，还是上面的误差像素位置误差形式，只不过优化变量变成三维点的坐标，这一步叫Structure -only Bundler Adjustment，优化过程中雅克比矩阵大小为2×32×3(横纵坐标u，vu，v分别对点坐标(x,y,z)变量求导)。

Discussion
论文讨论了该方法中的前几个步骤，讨论了如果使用传统的LK光流法的话，时间会增加，同时较大距离的跟踪需要较大的patch以及金字塔的应用，同时因为会存在跟丢的情况，因此需要外点检测，而在SVO的方法中，因为有feature alignment的步骤，使得特征点的位置还是比较准确的，因此能保证没有外点。

3 Mapping Thread

该线程中主要的工作就是判断当前帧是否可以作为key frame，之后进行深度滤波器的迭代以及初始化工作。下面主要说明深度滤波器的相关推导

3.1 depth-filter

最基本的深度估计就是三角化，这是多视角几何的基础内容(可以参看圣经Hartly的《Multiple View Geometry in Computer Vision》中的第十二章structure computation；可以参看我的相应博客)。我们知道通过两帧图像的匹配点就可以计算出这一点的深度值，如果有多幅图像，那就能计算出这一点的多个深度值。这就像对同一个状态变量我们进行了多次测量，因此，可以用贝叶斯估计来对多个测量值进行融合，使得估计的不确定性缩小。如下图所示：

一开始深度估计的不确定性较大(浅绿色部分)，通过三角化得到一个深度估计值以后，能够极大的缩小这个不确定性(墨绿色部分)。
  在这里，先简单介绍下svo中的三角化计算深度的过程，主要是极线搜索确定匹配点。在参考帧Ir中，我们知道了一个特征的图像位置，假设它的深度值在[dmin,dmax][dmin,dmax]之间，那么根据这两个端点深度值，我们能够计算出他们在当前帧Ik中的位置，如上图中草绿色圆圈中的线段。确定了特征出现的极线段位置，就可以进行特征搜索匹配了。如果极线段很短，小于两个像素，那直接使用上面求位姿时提到的Feature Alignment光流法就可以比较准确地预测特征位置。如果极线段很长，那分两步走，第一步在极线段上间隔采样，对采样的多个特征块一一和参考帧中的特征块匹配，用Zero mean Sum of Squared Differences 方法对各采样特征块评分，那个得分最高，说明他和参考帧中的特征块最匹配。第二步就是在这个得分最高点附近使用Feature Alignment得到次像素精度的特征点位置。像素点位置确定了，就可以三角化计算深度了。得到一个新的深度估计值以后，用贝叶斯概率模型对深度值更新。在LSD slam中，假设深度估计值服从高斯分布，用卡尔曼滤波(贝叶斯的一种)来更新深度值。这种假设中，他认为深度估计值效果很棒，很大的概率出现在真实值(高斯分布均值)附近。而SVO的作者采用的是Vogiatzis的论文《Video-based, real-time multi-view stereo》提到的概率模型，而在深度滤波器中，论文把真实深度的分布看做一个正态分布+均匀分布的模型

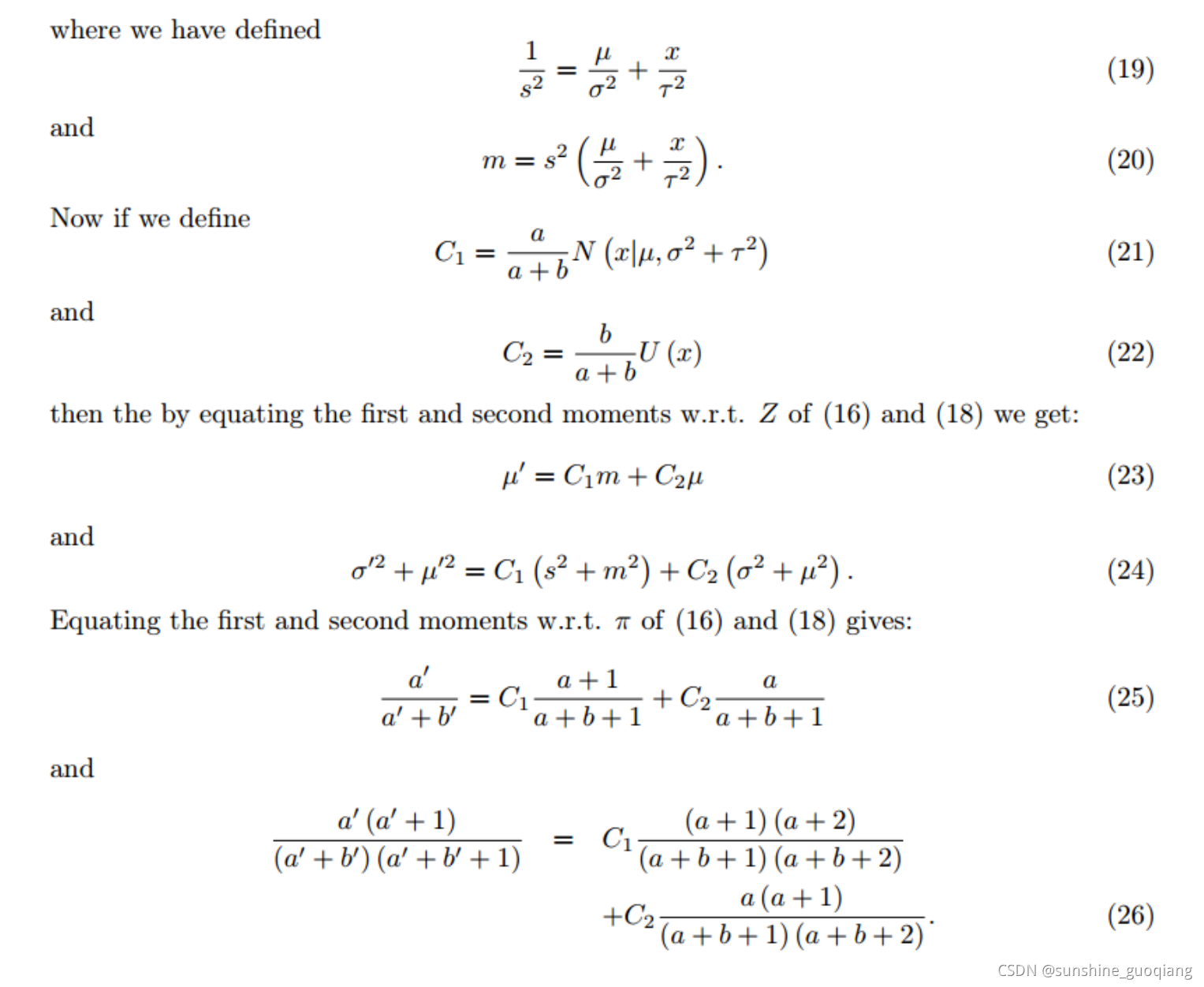
这个概率模型是一个高斯分布加上一个设定在最小深度dmindmin和最大深度dmaxdmax之间的均匀分布。这个均匀分布的意义是假设会有一定的概率出现错误的深度估计值。有关这个概率模型来由更严谨的论证去看看Vogiatzis的论文。同时，有关这个概率模型递推更新的过程具体可以看Vogiatzis在论文中提到的Supplementary material，论文中告知了下载地址。知道了这个贝叶斯概率模型的递推过程，程序就可以实现深度值的融合了，结合supplementary material去看svo代码中的updateSeeds(frame)这个程序就容易了，整个程序里的那些参数的计算递归过程的推导，我简单截个图，这部分我也没细看(公式19是错误的，svo作者指出了)，现在有几篇博客对该部分进行了推导。详见卢彦斌：svo原理解析,东北大学孙志明：svo的Supplementary matterial 推导过程](https://blog.csdn.net/u013004597/article/details/52069741)

在深度估计的过程中，除了计算深度值外，这个深度值的不确定性也是需要计算的，它在很多地方都会用到，如极线搜索中确定极线的起始位置和长度，如用贝叶斯概率更新深度的过程中用它来确定更新权重(就像卡尔曼滤波中协方差矩阵扮演的角色)，如判断这个深度点是否收敛了，如果收敛就插入地图等等。SVO的作者Forster作为第二作者发表的《REMODE: Probabilistic, Monocular Dense Reconstruction in Real Time》中对由于特征定位不准导致的三角化深度误差进行了分析，如上图。
它是通过假设特征点定位差一个像素偏差，来计算深度估计的不确定性。具体推导见原论文，简单的几何关系。

3.2 初始化

​ SVO的初始化过程：它假设前两个关键帧所拍到的特征点在一个平面上(四轴飞行棋对地面进行拍摄)，然后估计单应性H矩阵，并通过三角化来估计初始特征点的深度值。SVO初始化时triangulation的方法具体代码是vikit/math_utils.cpp里的triangulateFeatureNonLin()函数，使用的是中点法，关于这个三角化代码算法的推导见github issue。

还有就是SVO适用于摄像头垂直向下的情况（也就是无人机上,垂直向上也可以,朝着一面墙也可以），为什么呢？

1.初始化的时候假设的是平面模型
2.KF的选择是个极大的限制，除了KF的选择原因外摄像头水平朝前运动的时候，SVO中的深度滤波做的不好，这个讨论可以看看github issue，然而在我的测试中，不知道修改了哪些参数，稍微改动了部分代码，发现前向运动，并且对着非平面SVO也是很溜的。

参考：

[1] http://blog.csdn.net/heyijia0327
[2] https://blog.csdn.net/heyijia0327/article/details/51083398
[3] https://blog.csdn.net/u013004597/article/details/52069741
[4] SVO论文翻译总结
[5] http://rpg.ifi.uzh.ch/svo_pro.html
[6] https://www.cnblogs.com/wxt11/p/7097250.html