题目截图

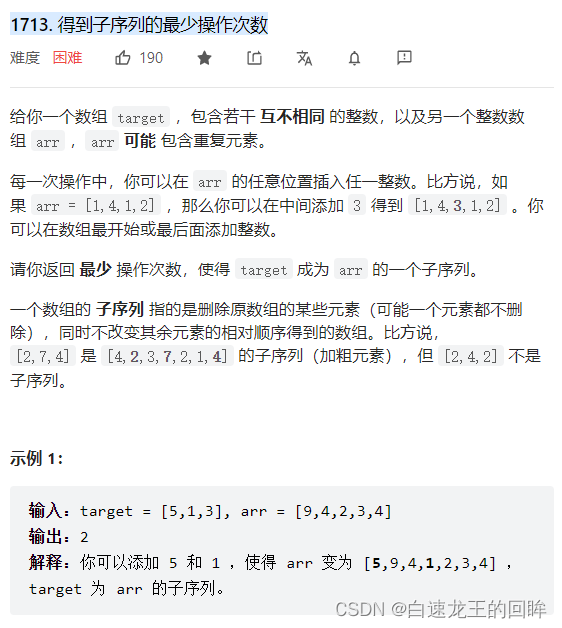
题目分析

• 就是要找最长公共子序列
• 典型的就是m * n的dp，但会超时
• 特别地，target不重复
• 因此，可以构造target的v和i的映射
• 遍历arr，得到target的下标顺序
• 使用【经典最长递增子序列二分法】得到最终的长度即可

ac code

class Solution:def minOperations(self, target: List[int], arr: List[int]) -> int:# 最长的公共子序列# target不重复，数字下标一一对应# 遍历arr，转化为找对应target下标最长递增子序列ids = {num: i for i, num in enumerate(target)}stack = []# 最长上升子序列for num in arr:if num in ids:id = ids[num]idx = bisect_left(stack, id)if idx == len(stack): # add to tailstack.append(id)else:stack[idx] = id # greedy changereturn len(target) - len(stack)

总结

• 最长公共子序列优化
• 下标映射
• 转化为最长递增子序列，递增保持target中也是一个子序列，最长递增即代表最长子序列