Question:
Come up with logic that counts number of ‘1’s in a 7 bit wide vector. You can only use combinational logic.
Answer:
Following is one of the ways to come up with such logic.
Input vector is 7 bit wide. To sum up 7 bits we need 3 bits of binary encoded output. We’ve full adders available. A single full adder can add 3 input bits and generate 2 bits of binary encoded output. E.g. a full adder can add 3 bit wide input vector ‘111’ and generate ‘11’ output. We can pick two full adders and add up 6 bits of the input vector and will end up with two sets of two bit wide binary encoded data. E.g. if input vector is ‘1100111’, we can assume two full adders adding up first 6 bits ‘110011’ where first three bits ‘110’ are input to first adder and ‘011’ are input to second adder. First adder will output ‘10’ (decimal 2) and second adder will also output ‘10’ (decimal 2), and we need to add up two two bit binary vectors. We can again employ full adders to do this as we still have to account for the 7th input bit of the input vector. That can go into the least significant full adder carry-input.
For the above example :
Input vector ‘1100111’
input ‘110’ => full adder => ‘10’ output
input ‘011’ => full adder => ‘10’ output
10
+10
------
100 => output (4)
Now accounting for the seventh input bit ‘1’ as carry into the least significant adder.
1 <= Carry in.
10
+10
-----
101 => Binary encoded decimal 5 which is the input of 1s in input vector ‘1100111’.
Full adders can be used to add-up 3 input bits at a time. Outputs of first level of full adders represent the two bit encoded version of the total ‘1’s count, which we need to add up get the final two digit encoded version of total ‘1’s. Since we need to add up 7 bit input vector, 7th input vector can be used as ‘Carry In’ in the second level of full adders.
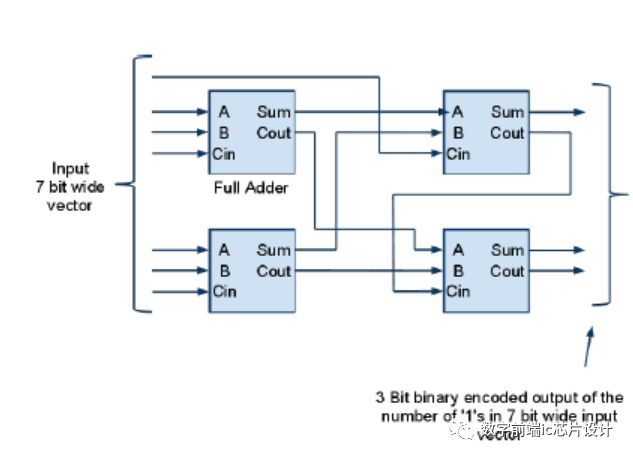 .
.
全加器:除本位两个数相加外,还要加上从低位来的进位数,称为全加器。带进位输入和输出的加法器,一位全加器三个输入分别是,两个加数和一个进位输入,输出为和以及向高位进位D