目录
- 0 写在前面
- 1 字典学习
- 2 问题形式化
- 3 KSVD算法
- 4 Python实现
0 写在前面
机器学习强基计划聚焦深度和广度,加深对机器学习模型的理解与应用。“深”在详细推导算法模型背后的数学原理;“广”在分析多个机器学习模型:决策树、支持向量机、贝叶斯与马尔科夫决策、强化学习等。强基计划实现从理论到实践的全面覆盖,由本人亲自从底层编写、测试与文章配套的各个经典算法,不依赖于现有库,可以大大加深对算法的理解。
🚀详情:机器学习强基计划(附几十种经典模型源码)
1 字典学习
人类社会一切已发现或未发现的知识都必须通过字、词、句进行表示,而整体的知识量非常庞大——人类每天产生的新知识约2T;换言之,无论人类的知识多么浩瀚,一本新华字典或牛津字典也足以表达人类从古至今乃至未来的所有知识——字典中字、词、句的排列组合。所以字典相当于庞大数据集的一种降维表示,且蕴藏样本背后最本质的特征。现代神经科学表明,哺乳动物大脑的初级视觉皮层主要工作就是进行图像的字典表示。
考虑样本矩阵的一种分解
X = D A \boldsymbol{X}=\boldsymbol{DA} X=DA
其中 X = [ x 1 x 2 ⋯ x m ] ∈ R d × m \boldsymbol{X}=\left[ \begin{matrix} \boldsymbol{x}_1& \boldsymbol{x}_2& \cdots& \boldsymbol{x}_m\\\end{matrix} \right] \in \mathbb{R} ^{d\times m} X=[x1x2⋯xm]∈Rd×m是样本矩阵; A = [ α 1 α 2 ⋯ α m ] ∈ R k × m \boldsymbol{A}=\left[ \begin{matrix} \boldsymbol{\alpha }_1& \boldsymbol{\alpha }_2& \cdots& \boldsymbol{\alpha }_m\\\end{matrix} \right] \in \mathbb{R} ^{k\times m} A=[α1α2⋯αm]∈Rk×m是样本 X \boldsymbol{X} X的编码矩阵,其中 α i \boldsymbol{\alpha }_i αi是 x i \boldsymbol{x}_i xi的编码; D = [ d 1 d 2 ⋯ d k ] ∈ R d × k \boldsymbol{D}=\left[ \begin{matrix} \boldsymbol{d}_1& \boldsymbol{d}_2& \cdots& \boldsymbol{d}_k\\\end{matrix} \right] \in \mathbb{R} ^{d\times k} D=[d1d2⋯dk]∈Rd×k称为字典(dictionary), d i \boldsymbol{d}_i di称为字典的一个原子(atom),通常经过归一化处理, k k k称为字典的词汇量,可由用户指定。设样本相当于字典而言相当庞大,即 m ≫ k m\gg k m≫k
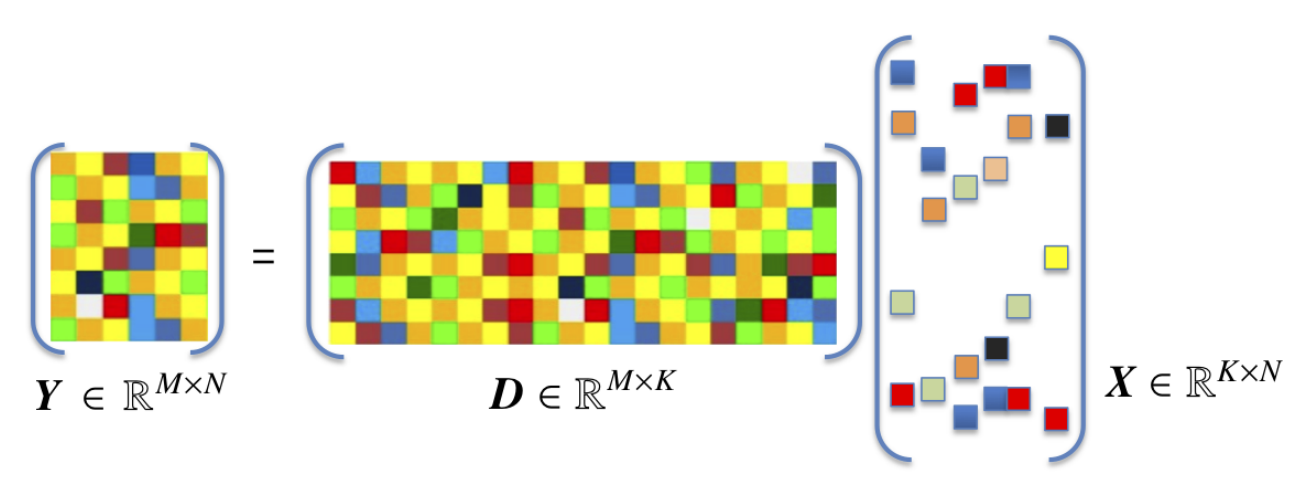
考察样本的编码形式:
- 若 k < d k<d k<d,则 D \boldsymbol{D} D称为欠完备字典,相当于特征选择或线性降维技术;
- 若 k > d k>d k>d,则 D \boldsymbol{D} D称为过完备字典,编码维度增大似乎违背了避免维数灾难的原则,但此时约束 α i \boldsymbol{\alpha }_i αi是 x i \boldsymbol{x}_i xi的稀疏表示(sparse representation)——含有大量零元素。
2 问题形式化
字典学习(dictionary learning)研究如何从普通稠密样本中学习出字典,并将样本转换为恰当稀疏的表示形式,从而简化学习任务、降低模型复杂度。形式化为
min D , α i ∑ i = 1 m ∥ x i − D α i ∥ 2 2 + λ ∑ i = 1 m ∥ α i ∥ 1 \underset{\boldsymbol{D},\boldsymbol{\alpha }_i}{\min}\sum_{i=1}^m{\left\| \boldsymbol{x}_i-\boldsymbol{D\alpha }_i \right\| _{2}^{2}}+\lambda \sum_{i=1}^m{\left\| \boldsymbol{\alpha }_i \right\| _1} D,αimini=1∑m∥xi−Dαi∥22+λi=1∑m∥αi∥1
字典学习可以分为两步:
- 固定字典对原始样本进行稀疏编码;
- 基于原始样本与稀疏表示更新字典。
关于稀疏表示和稀疏编码请参考机器学习强基计划9-1:图解匹配追踪(MP)与正交匹配追踪(OMP)算法
可见字典更新与稀疏编码在同一个优化过程中完成,字典学习的最终目标也是为了获得稠密样本的稀疏编码,因此不致混淆的情况下,字典学习与稀疏编码语义相同。本节重点介绍字典学习的第二步——字典更新。具体地,在给出稀疏编码后,优化问题变为
min D ∥ X − D A ∥ F 2 \min _{\boldsymbol{D}}\left\| \boldsymbol{X}-\boldsymbol{DA} \right\| _{F}^{2} Dmin∥X−DA∥F2
3 KSVD算法
KSVD算法的核心是利用奇异值分解SVD逐个更新字典原子。设 α i \boldsymbol{\alpha }^i αi表示稀疏矩阵 A \boldsymbol{A} A的第 i i i行,则优化问题等价于
min d 1 , ⋯ , d k ∥ X − ∑ i = 1 k d i α i ∥ F 2 \underset{\boldsymbol{d}_1,\cdots ,\boldsymbol{d}_k}{\min}\left\| \boldsymbol{X}-\sum_{i=1}^k{\boldsymbol{d}_i\boldsymbol{\alpha }^i} \right\| _{F}^{2} d1,⋯,dkmin X−i=1∑kdiαi F2
现固定住原子 d 1 , ⋯ , d i − 1 , d i + 1 , ⋯ , d k \boldsymbol{d}_1,\cdots ,\boldsymbol{d}_{i-1},\boldsymbol{d}_{i+1},\cdots ,\boldsymbol{d}_k d1,⋯,di−1,di+1,⋯,dk而只考虑对 d i \boldsymbol{d}_i di的优化,即
min d i ∥ ( X − ∑ j ≠ i d j α j ) − d i α i ∥ F 2 = min d i ∥ E i − d i α i ∥ F 2 \underset{\boldsymbol{d}_i}{\min}\left\| \left( \boldsymbol{X}-\sum_{j\ne i}{\boldsymbol{d}_j\boldsymbol{\alpha }^j} \right) -\boldsymbol{d}_i\boldsymbol{\alpha }^i \right\| _{F}^{2}=\underset{\boldsymbol{d}_i}{\min}\left\| \boldsymbol{E}_i-\boldsymbol{d}_i\boldsymbol{\alpha }^i \right\| _{F}^{2} dimin X−j=i∑djαj −diαi F2=dimin Ei−diαi F2
其中 E i = X − ∑ j ≠ i d j α j \boldsymbol{E}_i=\boldsymbol{X}-\sum\nolimits_{j\ne i}^{}{\boldsymbol{d}_j\boldsymbol{\alpha }^j} Ei=X−∑j=idjαj是固定值,此时转换为调整 d i α i \boldsymbol{d}_i\boldsymbol{\alpha }^i diαi使之逼近 E i \boldsymbol{E}_i Ei的最小二乘问题,因为改变了字典原子 d i \boldsymbol{d}_i di,所以全体样本第 i i i维的稀疏表示 α i \boldsymbol{\alpha }^i αi也要随之改变,而改变 α i \boldsymbol{\alpha }^i αi可能会破坏稀疏编码过程的稀疏性,因此工程上需要特别处理: α i \boldsymbol{\alpha }^i αi仅保留非零元素, E i \boldsymbol{E}_i Ei仅保留 d i \boldsymbol{d}_i di与 α i \boldsymbol{\alpha }^i αi非零元素的乘积项,如图所示。
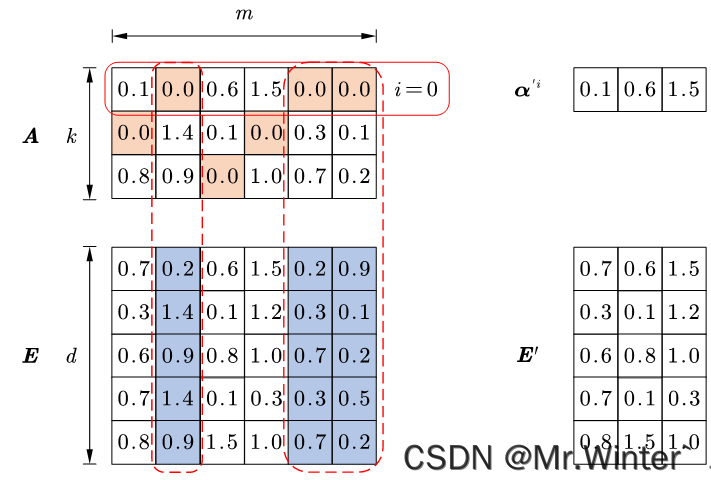
此时优化问题变为 min d i , α ′ i ∥ E i ′ − d i α ′ i ∥ F 2 \min _{\boldsymbol{d}_i,\boldsymbol{\alpha }^{'i}}\left\| \boldsymbol{E}_{i}^{'}-\boldsymbol{d}_i\boldsymbol{\alpha }^{'i} \right\| _{F}^{2} mindi,α′i Ei′−diα′i F2,在KSVD算法中对 E i ′ \boldsymbol{E}_{i}^{'} Ei′进行奇异值分解
E i ′ = U Σ V = [ u max ⋯ u d ] [ σ max ⋱ 0 ] [ v max T ⋮ v m ′ T ] \boldsymbol{E}_{i}^{'}=\boldsymbol{U\varSigma V}=\left[ \begin{matrix} \boldsymbol{u}_{\max}& \cdots& \boldsymbol{u}_d\\\end{matrix} \right] \left[ \begin{matrix} \sigma _{\max}& & \\ & \ddots& \\ & & 0\\\end{matrix} \right] \left[ \begin{array}{c} \boldsymbol{v}_{\max}^{T}\\ \vdots\\ \boldsymbol{v}_{m'}^{T}\\\end{array} \right] Ei′=UΣV=[umax⋯ud] σmax⋱0 vmaxT⋮vm′T
其中奇异值矩阵按照奇异值从大到小排列,此时令 d i = u max \boldsymbol{d}_i=\boldsymbol{u}_{\max} di=umax、 α ′ i = σ max v max T \boldsymbol{\alpha }^{'i}=\sigma _{\max}\boldsymbol{v}_{\max}^{T} α′i=σmaxvmaxT即可达到原问题的近似最小值。按上述步骤遍历字典原子即可更新字典。
4 Python实现
核心代码如下所示
def KSVD(Y, D, X, K):for k in range(K):index = np.nonzero(X[k, :])[0]if len(index) == 0:continuer = (Y - np.dot(D, X))[:, index]U, S, V_T = np.linalg.svd(r, full_matrices=False)D[:, k] = U[:, 0]for j, xj in enumerate(index):X[k, xj] = S[0] * V_T[0, j]return D, Xdef train(Ks, epoches):images = []# 初始化D,从Y中随机选取K列作为DU, _, _ = np.linalg.svd(Y)D = U[:, :K]for epoch in range(epoches):# 每一次更新D之后由OMP算法求得稀疏矩阵XX = linear_model.orthogonal_mp((D-D.min())/(D.max()-D.min()), Y)# KSVD算法更新DD, X = KSVD(Y, D, X, K)# 计算损失并输出L2_loss = (((Y - np.dot(D, X)) ** 2) ** 0.2).mean()# 最后一轮更新D之后还需要拟合一下新的XX = linear_model.orthogonal_mp((D-D.min())/(D.max()-D.min()), Y)# 重构图片rebuilded_image = np.clip(np.dot((D-D.min())/(D.max()-D.min()), X).reshape(*image.shape), 0, 1)images.append(rebuilded_image)return images
以图像重构为例说明字典学习的作用,如下所示,可以看出字典中原子量越多,重构效果越好。可以通过选择适当原子量的字典,实现对图像的压缩

完整代码通过下方名片联系博主获取
🔥 更多精彩专栏:
- 《ROS从入门到精通》
- 《Pytorch深度学习实战》
- 《机器学习强基计划》
- 《运动规划实战精讲》
- …