---

一、前言

最近做项目，需要判断一条线段是否和一段圆弧相交，网上也没找到很好的解答（最主要是没有直接可以搬来用的代码，或者思路写得太过高深，我看不懂），于是决定自己想一个方法，写一个博客，将实现思路和完整代码都分享出来

---

二、线段与圆弧的代码表示

2.1 线段代码表示

线段可用两个点表示，点的对象如下所示，包含x和y坐标信息：

class Point {
public:Point(double px=0.0, double py=0.0) {x = px;y = py;}double x;double y;
};

2.2 圆弧代码表示

圆弧由圆心坐标、半径、起始和终止角度组成：

class Arc
{
public:Point centerpoint; // 圆心double radius; // 圆弧半径double bangle; // 起点角度double eangle; // 终点角度
};

---

三、实现思路及数学推导

3.1 第一步（粗略判断）

第一步（粗略判断）：将线段当成直线，将圆弧当成圆，如果直线和圆不相交，则线段和圆弧必然不相交，否则进行下一步判断

首先，将线段扩展成一条直线，它的方程为：$y=kx+c$

根据线段的两个点（假设为 $p_1$ 和 $p_2$，且 $p_1.x\le p_2.x$）信息，我们可以很轻易求出 $k$ 和 $c$ 的取值

将$p_1$ 和 $p_2$ 代入直线方程：

$$\{\begin{array}{l}{p}_1.y=k{p}_1.x+c\left(1\right)\\ p_2.y=k{p}_2.x+c\left(2\right)\end{array}$$

$(1)-(2)$ 可得：

$$\begin{gathered} p_1.y-p_2.y=\left(p_1.x-p_2.x\right)k \\ \Rightarrow k=\frac{p_1.y-p_2.y}{p_1.x-p_2.x}\left(3\right) \end{gathered}$$

将 $(3)$ 代入 $(1)$ 可得：

$$\begin{gathered} p_1.y=\frac{p_1.y-p_2.y}{p_1.x-p_2.x}{p}_1.x+c \\ \Rightarrow c=p_1.y-\frac{p_1.y-p_2.y}{p_1.x-p_2.x}{p}_1.x\left(4\right) \end{gathered}$$

假设圆心坐标为 $(a,b)$ ，半径为 $r$ ，容易写出圆弧扩展而成的圆的方程如下所示：

$$(x-a{)}^2+(y-b{)}^2=r^2\left(5\right)$$

要判断直线和圆是否相交，需要将直线方程和圆方程进行联立得：

$$\begin{gathered} \{\begin{array}{l}y=kx+c\\ (x-a{)}^2+(y-b{)}^2=r^2\end{array} \\ \Downarrow \\ (x-a{)}^2+(kx+c-b{)}^2=r^2,令d=c-b \\ \Downarrow \\ {x}^2+a^2-2ax+k^2{x}^2+d^2+2kdx=r^2 \\ \Downarrow \\ (1+k^2)x^2+(2kd-2a)x+a^2+d^2-r^2=0\left(6\right) \end{gathered}$$

根据韦达定理判断一元二次方程 $(6)$ 是否存在实数根：

$$\Delta =(2kd-2a{)}^2-4(1+k^2)(a^2+d^2-r^2)\Rightarrow \{\begin{array}{l}\Delta <0:式(6)不存在实数根\\ \Delta \ge 0:式(6)存在实数根\end{array}$$

如果式 $(6)$ 不存在实数根，意味着直线和圆没有交点，此时线段和圆弧必然也没有交点，程序结束。

如果式 $(6)$ 存在实数根，则可以解出直线与圆的两个交点的 $X$ 方向坐标 $x_1$ 和 $x_2$：

$$x_1=\frac{-(2kd-2a)+\sqrt{\Delta }}{2(1+k^2)}和x_2=\frac{-(2kd-2a)-\sqrt{\Delta }}{2(1+k^2)}$$

将 $x_1$ 和 $x_2$ 分别代入直线方程 $y=kx+c$ 可得两个交点的 $Y$ 方向坐标 $y_1$ 和 $y_2$：

$$y_1=k{x}_1+c和y_2=k{x}_2+c$$

然后进行下一步判断

3.2 第二步

第二步：判断直线和圆的两个交点是否在线段上，如果不在，说明线段和圆弧必然不相交，否则进行下一步判断

线段是连续的，所以可以通过区间判断两个交点是否在线段上

详细地说，我们已经知道线段的X轴方向的区间为 $[p_1.x,p_2.x]$

如果 $x_1$ 不在 $[p_1.x,p_2.x]$ 区间内，则点 $(x_1,y_1)$ 不在线段上，也就不可能是线段和圆弧的交点

同理，如果 $x_2$ 不在 $[p_1.x,p_2.x]$ 区间内，则点 $(x_2,y_2)$ 也不可能是线段和圆弧的交点

如果点 $(x_1,y_1)$ 和点 $(x_2,y_2)$ 都不是线段和圆弧的交点，则说明线段和圆弧必然不相交

否则进行下一步判断

3.3 第三步

第三步：根据前面的推导，假设已知直线和圆的一个在线段上的交点为 $(x_1,y_1)$，在这一步中，需要判断该点是否在圆弧上，如果在，则说明线段和圆弧相交，且交点为 $(x_1,y_1)$

在这一步中，需要使用圆的参数方程，为了方便表示，假设圆弧的起始角度和终止角度分别为 ${\theta }_1$ 和 ${\theta }_2$，则圆弧的参数方程为：

$$\{\begin{array}{l}x=a+rcos\theta \left(7\right)\\ y=b+rsin\theta \left(8\right)\end{array},{\theta }_1\le \theta \le {\theta }_2$$

将 $(x_1,y_1)$ 代入式 $(7)$ 和式 $(8)$ 中：

$$\begin{gathered} \{\begin{array}{l}{x}_1=a+rcos\theta \\ y_1=b+rsin\theta \end{array},{\theta }_1\le \theta \le {\theta }_2 \\ \Downarrow \\ \{\begin{array}{l}{x}_1-a=rcos\theta \left(9\right)\\ y_1-b=rsin\theta \left(10\right)\end{array},{\theta }_1\le \theta \le {\theta }_2 \end{gathered}$$

$(10)$➗$(9)$ 可得：

$$\begin{gathered} \frac{y_1-b}{x_1-a}=tan\theta \\ \Downarrow \\ \theta =arctan(\frac{y_1-b}{x_1-a}) \end{gathered}$$

如果解出的 $\theta$ 不在区间 $[{\theta }_1,{\theta }_2]$ 内，则说明点 $(x_1,y_1)$ 不在圆弧上

否则，点 $(x_1,y_1)$ 在圆弧上，并且是线段和圆弧的一个交点

至此，证毕！

注意：使用 $atan$ 函数计算反正切值时，返回值的取值范围是 $[-\frac{\pi }{2},\frac{\pi }{2}]$，而 $\theta$ 的取值是 $[0,2\pi ]$，所以在实际代码中需要对角度进行转换

---

四、完整代码

// 圆周率
#define PI acos(-1)
// 浮点型数据精度
#define ERROR 0.0000001// lineIsIntersectArc 的辅助函数：接着第二步判断
bool lineIsIntersectArcAuxiliaryFunction(Point p1, Point p2, double a, double b, double theta1, double theta2, double x1, double y1){// 2.3 判断交点是否在线段上if (p1.x <= x1 && x1 <= p2.x){// 第三步：交点(x1,y1)在线段上，再判断该点是否在圆弧上，如果在，则说明线段和圆弧相交，且交点为(x1,y1)// 3,1 计算 theta ，并转化为角度值double theta = atan((y1 - b) / (x1 - a)) / PI * 180.0;// 3.2 修正角度值，确保 theta1 <= theta2if (theta1 > theta2){if (theta2 >= 0){theta1 -= 360;}else{theta2 += 360;}			}if (theta1 < 0 && theta2 < 0){theta1 += 360;theta2 += 360;}// 3.3 修正 tan 的角度if (x1 < a){theta += 180;}// 3.4 在端点时，由于精度误差，有时可能会出现判断出错 (即出现 10.000000001 > 10 的情况)，故以极小的误差接受(x1,y1)为圆弧的某个端点if (abs(theta1 - theta) < ERROR || abs(theta2 - theta) < ERROR){return true;}// 3.5 判断 theta 是否在圆弧范围内，如果在则(x1,y1)是线段和圆弧的交点，否则不是return theta1 <= theta && theta <= theta2;}return false;
}// 判断一个线段是否和圆弧相交
bool lineIsIntersectArc(Point p1, Point p2, Arc arc){// 确保 p1.x <= p2.xif (p1.x > p2.x){DL_VertexData temp = p1;p1 = p2;p2 = temp;}// 简化圆弧的相关变量表示double a = arc.centerpoint.x;double b = arc.centerpoint.y;double r = arc.radius;double theta1 = arc.bangle;double theta2 = arc.eangle;// 第一步（粗略判断）：将线段当成直线，将圆弧当成圆，如果直线和圆不相交，则线段和圆弧必然不相交，否则进行下一步判断// 1.1 根据公式，计算直线方程 y=kx+c 中的 k 和 cdouble k = (p1.y - p2.y) / (p1.x - p2.x);double c = p1.y - (p1.y - p2.y) / (p1.x - p2.x)*p1.x;// 1.2 根据韦达定理判断式（6）是否存在实数根double d = c - b;double varDelta = pow(2 * k*d-2*a, 2) - 4 * (1 + k*k)*(a*a + d*d - r*r);if (varDelta >= 0){// 第二步：判断直线和圆的两个交点是否在线段上，如果不在，说明线段和圆弧必然不相交，否则进行下一步判断// 2.1 计算两个交点的坐标(x1,y1)和(x2,y2)double x1 = (2 * a - 2 * k*d + sqrt(varDelta)) / (2 * (1 + k*k));double x2 = (2 * a - 2 * k*d - sqrt(varDelta)) / (2 * (1 + k*k));double y1 = k*x1 + c;double y2 = k*x2 + c;// 2.2 判断两个交点是否相等if (varDelta == 0){// 两个交点相等，只需要判断一个就好return lineIsIntersectArcAuxiliaryFunction(p1, p2, a, b, theta1, theta2, x1, y1);}else{// 两个交点不相等，分别进行判断，只要其中一个是线段和圆弧的交点就返回 truereturn lineIsIntersectArcAuxiliaryFunction(p1, p2, a, b, theta1, theta2, x1, y1) || lineIsIntersectArcAuxiliaryFunction(p1, p2, a, b, theta1, theta2, x2, y2);}}return false;
}

---

五、效果展示

有了判断一条线段和一段圆弧是否相交的函数之后，就可以用来判断圆弧是否和一个多边形相交了。最简单的思路就是用圆弧和多边形的每个边依次做判断，如果多边形的任意一条边和圆弧都不相交，则圆弧与多边形必然不相交。

交叉判断前，从下图可以看到，黄色部分就是圆弧和多边形出现了交叉重叠的情况

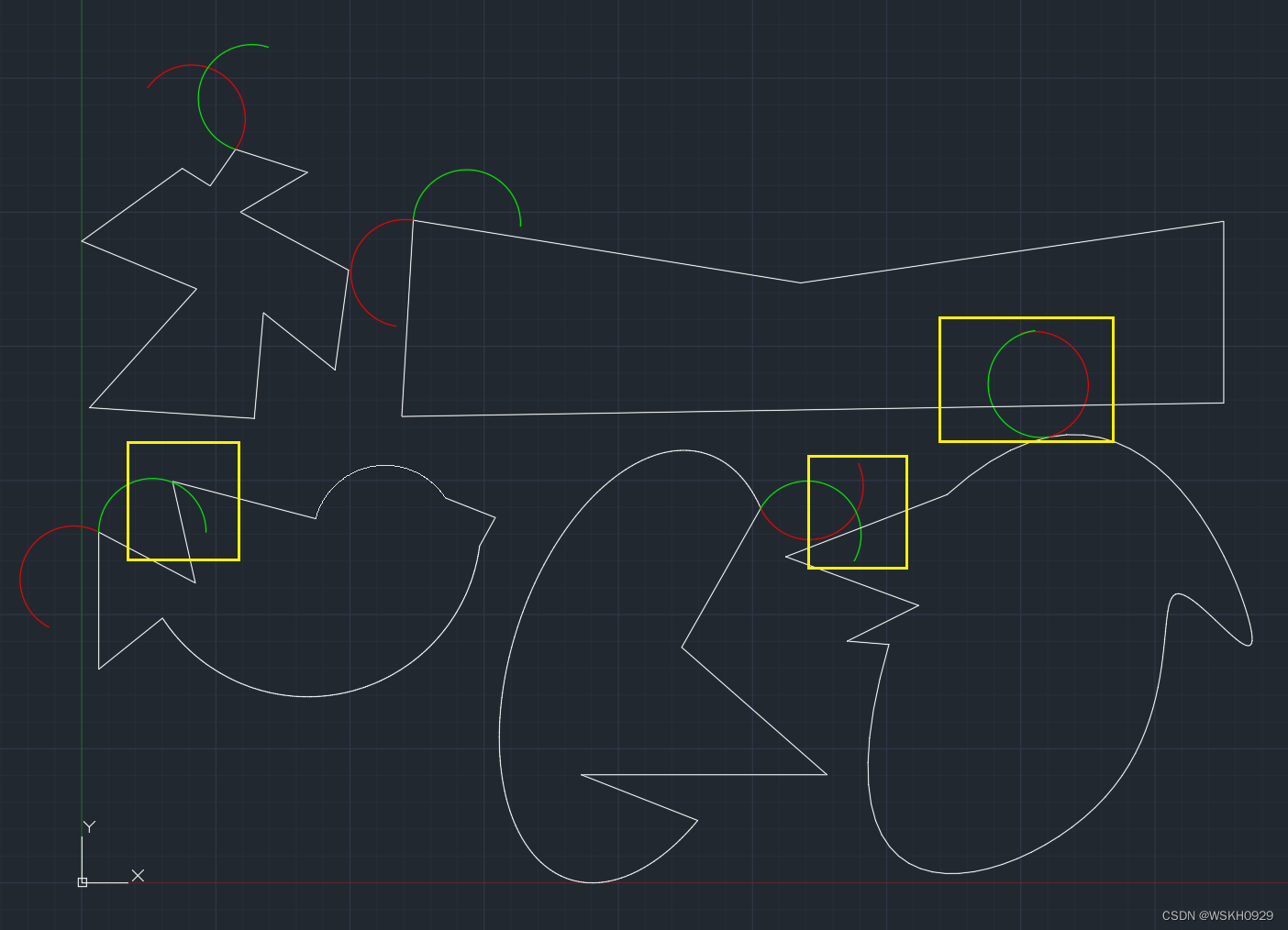
交叉判断后，圆弧与多边形的交叉情况完全消失~