SENet是ImageNet 2017（ImageNet收官赛）的冠军模型，和ResNet的出现类似，都在很大程度上减小了之前模型的错误率（具体见附录），并且复杂度低，新增参数和计算量小。下面就来具体介绍一些SENet的神奇之处。

SENet的全称是Squeeze-and-Excitation Networks，中文可以翻译为压缩和激励网络。主要由两部分组成：

1. Squeeze部分。即为压缩部分，原始feature map的维度为HWC，其中H是高度（Height），W是宽度（width），C是通道数（channel）。Squeeze做的事情是把HWC压缩为11C，相当于把HW压缩成一维了，实际中一般是用global average pooling实现的。HW压缩成一维后，相当于这一维参数获得了之前H*W全局的视野，感受区域更广。

2. Excitation部分。得到Squeeze的11C的表示后，加入一个FC全连接层（Fully Connected），对每个通道的重要性进行预测，得到不同channel的重要性大小后再作用（激励）到之前的feature map的对应channel上，再进行后续操作。

我们可以看到，已经有很多工作在空间维度上来提升网络的性能。那么很自然想到，网络是否可以从其他层面来考虑去提升性能，比如考虑特征通道之间的关系？我们的工作就是基于这一点并提出了 Squeeze-and-Excitation Networks（简称 SENet）。在我们提出的结构中，Squeeze 和 Excitation 是两个非常关键的操作，所以我们以此来命名。我们的动机是希望显式地建模特征通道之间的相互依赖关系。另外，我们并不打算引入一个新的空间维度来进行特征通道间的融合，而是采用了一种全新的「特征重标定」策略。具体来说，就是通过学习的方式来自动获取到每个特征通道的重要程度，然后依照这个重要程度去提升有用的特征并抑制对当前任务用处不大的特征。

可以看出，SENet和ResNet很相似，但比ResNet做得更多。ResNet只是增加了一个skip connection，而SENet在相邻两层之间加入了处理，使得channel之间的信息交互成为可能，进一步提高了网络的准确率。

1)首先**Ftr这一步是转换操作（严格讲并不属于SENet，而是属于原网络，**可以看后面SENet和Inception及ResNet网络的结合），在文中就是一个标准的卷积操作而已，输入输出的定义如下表示。

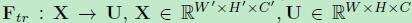
那么这个Ftr的公式就是下面的公式1（卷积操作，vc表示第c个卷积核，xs表示第s个输入）。

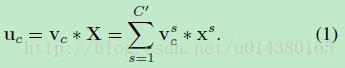
Ftr得到的U就是Figure1中的左边第二个三维矩阵，也叫tensor，或者叫C个大小为H*W的feature map。而uc表示U中第c个二维矩阵，下标c表示channel。

2)接下来就是Squeeze操作，公式非常简单，就是一个global average pooling

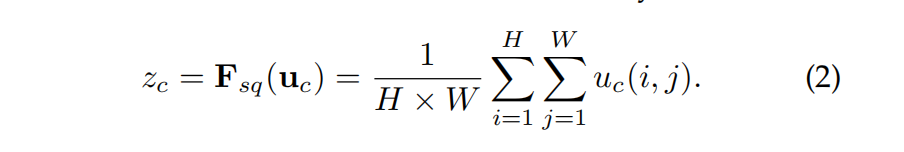
因此公式2就将HWC的输入转换成11C的输出，对应Figure1中的Fsq操作。为什么会有这一步呢？这一步的结果相当于表明该层C个feature map的数值分布情况，或者叫全局信息。

再接下来就是Excitation操作，如公式3。直接看最后一个等号，前面squeeze得到的结果是z，**这里先用W1乘以z，就是一个全连接层操作，W1的维度是C/r * C，这个r是一个缩放参数，在文中取的是16，**这个参数的目的是为了减少channel个数从而降低计算量。又因为z的维度是11C，所以W1z的结果就是11C/r；然后再经过一个ReLU层，输出的维度不变；然后再和W2相乘，**和W2相乘也是一个全连接层的过程，W2的维度是CC/r，因此输出的维度就是11*C；**最后再经过sigmoid函数，得到s。

也就是说最后得到的这个s的维度是11C，C表示channel数目。这个s其实是本文的核心，它是用来刻画tensor U中C个feature map的权重。而且这个权重是通过前面这些全连接层和非线性层学习得到的，因此可以end-to-end训练。这两个全连接层的作用就是融合各通道的feature map信息，因为前面的squeeze都是在某个channel的feature map里面操作。

在得到s之后，就可以对原来的tensor U操作了，就是下面的公式4。也很简单，就是channel-wise multiplication，什么意思呢？uc是一个二维矩阵，sc是一个数，也就是权重，因此相当于把uc矩阵中的每个值都乘以sc。对应Figure1中的Fscale。


Figure2是在Inception中加入SE block的情况，这里的Inception部分就对应Figure1中的Ftr操作。
Figure3是在ResNet中添加SE block的情况。

看完结构，再来看添加了SE block后，模型的参数到底增加了多少。其实从前面的介绍可以看出增加的参数主要来自两个全连接层，两个全连接层的维度都是C/r * C，那么这两个全连接层的参数量就是2*C^2/r。以ResNet为例，假设ResNet一共包含S个stage，每个Stage包含N个重复的residual block，那么整个添加了SE block的ResNet增加的参数量就是下面的公式：

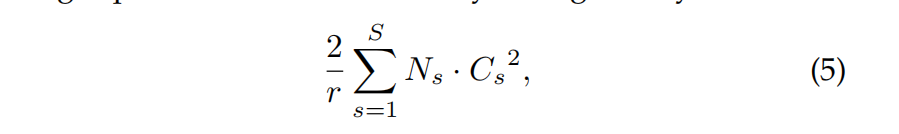
除了公式介绍，文中还举了更详细的例子来说明参数增加大概是多少百分比：In total, SE-ResNet-50 introduces 2.5 million additional parameters beyond the 25 million parameters required by ResNet-50, corresponding to a 10% increase in the total number of parameters。而且从公式5可以看出，增加的参数和C关系很大，而网络越到高层，其feature map的channel个数越多，也就是C越大，因此大部分增加的参数都是在高层。**同时作者通过实验发现即便去掉最后一个stage的SE block，对模型的影响也非常小（<0.1% top-1 error），**因此如果你对参数量的限制要求很高，倒是可以这么做，毕竟具体在哪些stage，哪些block中添加SE block都是自由定义的。
准确率结果：