概述

二叉树作为一个基础的数据结构，遍历算法作为一个基础的算法，两者结合当然是经典的组合了。很多题目都会有 ta 的身影，有直接问二叉树的遍历的，有间接问的。比如要你找到树中满足条件的节点，就是间接考察树的遍历，因为你要找到树中满足条件的点，就需要进行遍历。

你如果掌握了二叉树的遍历，那么也许其他复杂的树对于你来说也并不遥远了

二叉数的遍历主要有前中后遍历和层次遍历。 前中后属于 DFS，层次遍历则可以使用 BFS 或者 DFS 来实现。只不过使用 BFS 来实现层次遍历会容易些，因为层次遍历就是 BFS 的副产物啊，你可以将层次遍历看成没有提前终止的 BFS。

DFS 和 BFS 都有着自己的应用，比如 leetcode 301 号问题和 609 号问题。

DFS 都可以使用栈来简化操作，并且其实树本身是一种递归的数据结构，因此递归和栈对于 DFS 来说是两个关键点。

DFS 图解：

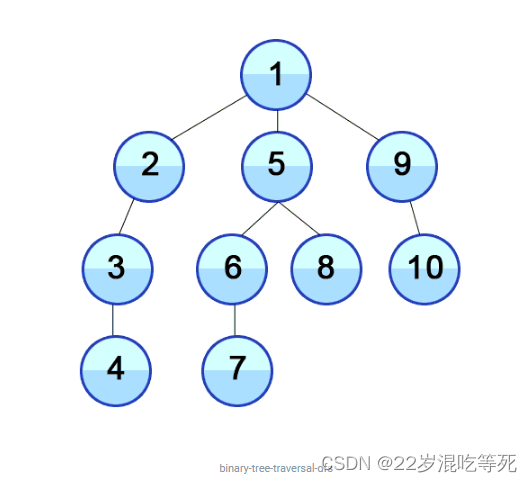
BFS 的关键点在于如何记录每一层次是否遍历完成， 我们可以用一个标识位来表式当前层的结束。

对于前中后序遍历来说。首先不管是前中还是后序遍历，变的只是根节点的位置， 左右节点的顺序永远是先左后右。 比如前序遍历就是根在前面，即根左右。中序就是根在中间，即左根右。后序就是根在后面，即左右根。

下面我们依次讲解：

前序遍历

相关问题144.binary-tree-preorder-traversal
前序遍历的顺序是根-左-右

思路是：

• 先将根结点入栈
• 出栈一个元素，将右节点和左节点依次入栈
• 重复 2 的步骤

总结： 典型的递归数据结构，典型的用栈来简化操作的算法。

其实从宏观上表现为：自顶向下依次访问左侧链，然后自底向上依次访问右侧链，如果从这个角度出发去写的话，算法就不一样了。从上向下我们可以直接递归访问即可，从下向上我们只需要借助栈也可以轻易做到。

整个过程大概是这样：

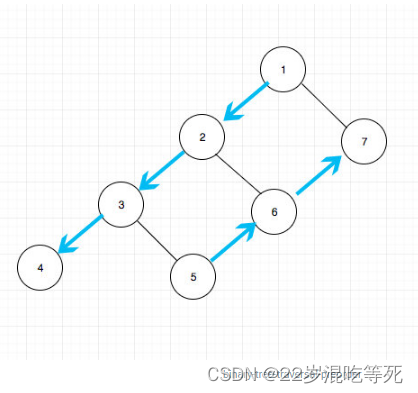
这种思路有一个好处就是可以统一三种遍历的思路. 这个很重要，如果不了解的朋友，希望能够记住这一点。

中序遍历

相关问题94.binary-tree-inorder-traversal
中序遍历的顺序是 左-根-右，根节点不是先输出，这就有一点点复杂了。

• 根节点入栈
• 判断有没有左节点，如果有，则入栈，直到叶子节点

此时栈中保存的就是所有的左节点和根节点。

1. 出栈，判断有没有右节点，有则入栈，继续执行 2

值得注意的是，中序遍历一个二叉查找树（BST）的结果是一个有序数组，利用这个性质有些题目可以得到简化， 比如230.kth-smallest-element-in-a-bst， 以及98.validate-binary-search-tree

后序遍历

相关问题145.binary-tree-postorder-traversal
后序遍历的顺序是 左-右-根
这个就有点难度了，要不也不会是 leetcode 困难的 难度啊。

其实这个也是属于根节点先不输出，并且根节点是最后输出。 这里可以采用一种讨巧的做法， 就是记录当前节点状态，如果：

• 当前节点是叶子节点或者
• 当前节点的左右子树都已经遍历过了，那么就可以出栈了。

对于 1. 当前节点是叶子节点或者当前节点的左右子树都已经遍历过了，那么就可以出栈了。
对于 2. 当前节点的左右子树都已经遍历过了， 只需要用一个变量记录即可。最坏的情况，我们记录每一个节点的访问状况就好了，空间复杂度 O(n) 但是仔细想一下，我们使用了栈的结构，从叶子节点开始输出，我们记录一个当前出栈的元素就好了，空间复杂度 O(1)， 具体请查看上方链接。

层次遍历

层次遍历的关键点在于如何记录每一层次是否遍历完成， 我们可以用一个标识位来表式当前层的结束。

具体做法：

• 根节点入队列， 并入队列一个特殊的标识位，此处是 null
• 出队列
• 判断是不是 null， 如果是，则代表本层已经结束。我们再次判断是否当前队列为空，如果不为空继续入队一个 null，否则说明遍历已经完成，我们什么都不不用做
• 如果不为 null，说明这一层还没完，则将其左右子树依次入队列。

相关问题：

双色标记法

我们知道垃圾回收算法中，有一种算法叫三色标记法。 即：

• 用白色表示尚未访问
• 灰色表示尚未完全访问子节点
• 黑色表示子节点全部访问

那么我们可以模仿其思想，使用双色标记法来统一三种遍历。

其核心思想如下：

• 使用颜色标记节点的状态，新节点为白色，已访问的节点为灰色。
• 如果遇到的节点为白色，则将其标记为灰色，然后将其右子节点、自身、左子节点依次入栈。
• 如果遇到的节点为灰色，则将节点的值输出。

使用这种方法实现的中序遍历如下：

class Solution:def inorderTraversal(self, root: TreeNode) -> List[int]:WHITE, GRAY = 0, 1res = []stack = [(WHITE, root)]while stack:color, node = stack.pop()if node is None: continueif color == WHITE:stack.append((WHITE, node.right))stack.append((GRAY, node))stack.append((WHITE, node.left))else:res.append(node.val)return res

可以看出，实现上 WHITE 就表示的是递归中的第一次进入过程，Gray 则表示递归中的从叶子节点返回的过程。 因此这种迭代的写法更接近递归写法的本质。

如要实现前序、后序遍历，只需要调整左右子节点的入栈顺序即可。可以看出使用三色标记法， 其写法类似递归的形式，因此便于记忆和书写，缺点是使用了额外的内存空间。不过这个额外的空间是线性的，影响倒是不大。

虽然递归也是额外的线性时间，但是递归的栈开销还是比一个 0，1 变量开销大的。换句话说就是空间复杂度的常数项是不同的，这在一些情况下的差异还是蛮明显的。

划重点：双色迭代法是一种可以用迭代模拟递归的写法，其写法和递归非常相似，要比普通迭代简单地多。

Morris 遍历

我们可以使用一种叫做 Morris 遍历的方法，既不使用递归也不借助于栈。从而在 $O(1)$ 空间完成这个过程。

如果你需要使用 $O(1)$ 空间遍历一棵二叉树，那么就要使用 Morris 遍历。

这个算法考察相对少，作为了解即可。

def MorrisTraversal(root):curr = rootwhile curr:# If left child is null, print the# current node data. And, update# the current pointer to right child.if curr.left is None:print(curr.data, end= " ")curr = curr.rightelse:# Find the inorder predecessorprev = curr.leftwhile prev.right is not None and prev.right is not curr:prev = prev.right# If the right child of inorder# predecessor already points to# the current node, update the# current with it's right childif prev.right is curr:prev.right = Nonecurr = curr.right# else If right child doesn't point# to the current node, then print this# node's data and update the right child# pointer with the current node and update# the current with it's left childelse:print (curr.data, end=" ")prev.right = currcurr = curr.left

划重点：Morris 是一种可以在 $O(1)$ 空间遍历二叉树的算法。

总结

本文详细讲解了二叉树的层次遍历和深度优先遍历。

对于深度优先遍历，我们又细分为前中后序三种遍历方式。

最后我们讲解了双色遍历和 Morris 遍历。这两种方式可以作为了解，不掌握也没关系。

另外，如果题目要求你实现迭代器（就是调用一次输出一个二叉树的值），那么前面讲的迭代的方式就非常适用了。比如这道题 Binary Search Tree Iterator