一问题描述

杰克逊被邀请参加电视节目“超强记忆”，参与者会玩一个记忆游戏。主持人先告诉参与者一个数字序列 {A1 , A2 , …, An }，然后对该序列执行一系列操作或查询：

① ADD x y D ，表示对子序列 {Ax , …, Ay } 的每个数字都增加 D ，例如在序列 {1, 2, 3, 4, 5} 上执行 ADD 2 4 1，结果为 {1, 3, 4, 5, 5}；

② REVERSE x y ，表示反转子序列 {Ax , …, Ay}，例如在序列 {1, 2,3, 4, 5} 上执行 REVERSE 2 4，结果为 {1, 4, 3, 2, 5}；

③ REVOLVE x y T ，表示旋转子序列 {Ax , …, Ay } T 次，例如在序列 {1, 2, 3, 4,5} 上执行 REVOLVE 2 4 2，结果为 {1, 3, 4, 2, 5}；

④ INSERT x P ，表示在 Ax 后插入 P ，例如在序列 {1, 2, 3, 4, 5} 上执行 INSERT 2 4，结果为 {1, 2, 4, 3, 4, 5}；

⑤ DELETE x ，表示删除 Ax ，例如在序列 {1, 2, 3, 4, 5} 上执行 DELETE 2，结果为 {1, 3, 4, 5}；

⑥ MIN x y，表示查询子序列 {Ax , …, Ay } 的最小数值，例如在序列 {1, 2, 3,4, 5} 上执行 MIN 2 4，结果为 2。

为了使节目更有趣，参与者有机会求助他人。请写一个程序，正确回答每个问题，以便在杰克逊打电话时帮助他。

二输入

第 1 行输入数字 n（n≤10^5 ）；接下来输入 n 行描述数字序列；接着输入数字 M（M≤10^5 ），表示操作或查询的数量；然后输入 M 行描述操作或查询。

三输出

对每个 MIN 查询都输出正确的答案。

四输入和输出样例

1 输入样例

5

1

2

3

4

5

2

ADD 2 4 1

MIN 4 5

2 输出样例

5

五分析

本问题涉及 6 种操作：插入、删除、区间查询、区间修改、区间反转、区间旋转，完美诠释了伸展树的神通广大。

六设计

1 插入

在第 pos 个元素后插入一个元素 val，将 Apos 旋转到根部，再将 Apos+1 旋转到 Apos 下方，最后在 Apos+1 的左子树中插入新节点 val 即可。

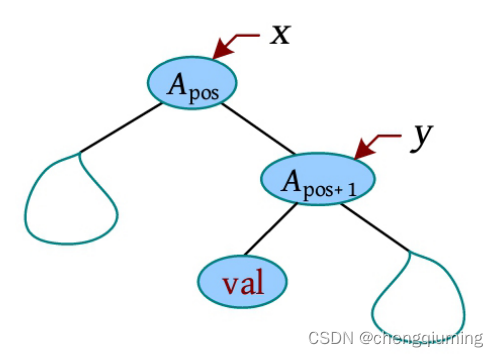
2 删除

删除第 pos 个元素，将 pos-1 旋转到根部，再将 Apos+1 旋转到 Apos-1 下方，此时 Apos 就是 Apos+1 的左子树，直接删除即可。

3 区间查询

查询 [l , r] 区间的最小值时，只需将 Al-1 旋转到根，然后将 Ar+1 旋转到 Al-1 的下方，此时需要查询的 [l , r] 区间就是 Ar+1 的左子树，输出该节点的最小值即可。

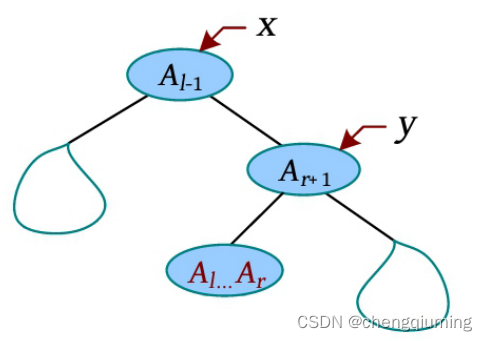
4 区间修改

和区间查询类似，将 [l , r] 区间的所有元素都增加 val，只需将 Al-1 旋转到根，然后将 Ar+1 旋转到 Al-1 的下方，此时需要增加的 [l , r] 区间就是 Ar+1 的左子树，修改该 [l,r] 区间的根节点（值、区间最小值、懒标记），懒标记会在下次访问时下传。

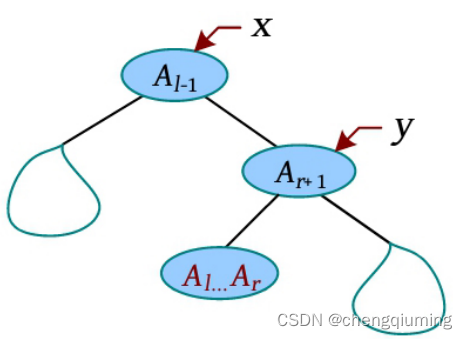
5 区间反转

和区间查询类似，反转 [l,r] 区间时，只需将 Al-1 旋转到根，然后将 Ar+1 旋转到 Al-1 的下方，此时需要反转的 [l, r ]区间就是 Ar+1 的左子树，在该区间的根节点打上反转懒标记即可。

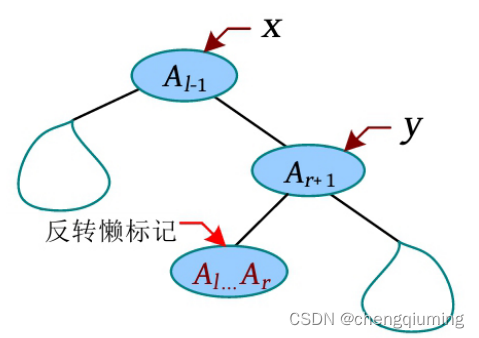
6 区间旋转

旋转[l,r] 区间 T 次，即将 [l,r] 区间循环右移 T 次，相当于将 [r-T+1,r] 区间的元素移动到 Al-1 之后。

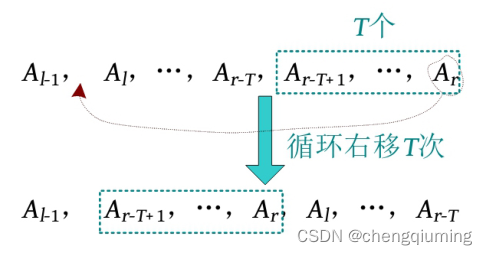
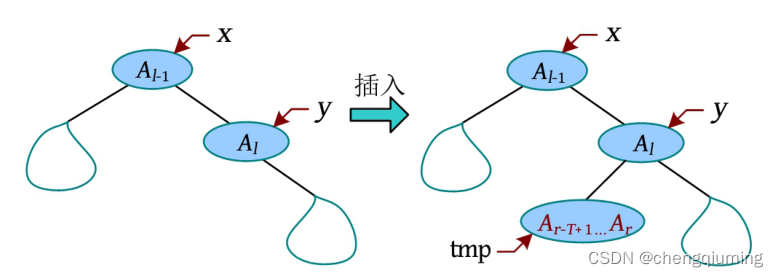
可以将该 [r-T+1,r] 区间暂存后删除，再插入Al-1 之后。首先将 Ar-T 旋转到根，然后将 Ar+1 旋转到 Ar-T 的下方，此时 [r-T+1 , r] 区间就是 Ar+1 的左子树，将其暂存给 tmp 后删除。

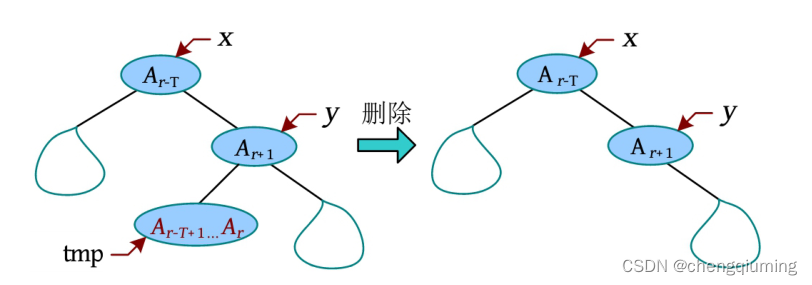
然后将 tmp 插入 Al-1 之后。只需将 Al-1 旋转到根，然后将 Al 旋转到 Al-1 的下方，将 tmp 挂接到 Al 的左子树上，即可完成插入操作。

因为 T 有可能超过 [l , r]区间的长度（m=r-l +1），所以只需 T=T%m 。若 T 有可能为负值，则可以通过 T=(T+m )%m 处理。

七代码

package com.platform.modules.alg.alglib.poj3580;public class Poj3580 {public String output = "";private int maxn = 200100;private int inf = 0x3f3f3f3f;int n, cnt, root; // 结点数，结点存储下标累计，树根int a[] = new int[maxn];String op;private node tr[] = new node[maxn];public String cal(String input) {int m, l, r, val;String[] line = input.split("\n");n = Integer.parseInt(line[0]);for (int i = 1; i <= n; i++) {a[i] = Integer.parseInt(line[i]);}Init();m = Integer.parseInt(line[n + 1]);int count = n + 2;while (m-- > 0) {String[] command = line[count++].split(" ");op = command[0];if (op.charAt(0) == 'A') {l = Integer.parseInt(command[1]);r = Integer.parseInt(command[2]);val = Integer.parseInt(command[3]);Add(++l, ++r, val);} else if (op.charAt(0) == 'M') {l = Integer.parseInt(command[1]);r = Integer.parseInt(command[2]);output += Min(++l, ++r) + "\n";} else if (op.charAt(0) == 'I') {l = Integer.parseInt(command[1]);val = Integer.parseInt(command[2]);Insert(++l, val);} else if (op.charAt(0) == 'D') {l = Integer.parseInt(command[1]);Delete(++l);} else if (op.charAt(0) == 'E') {l = Integer.parseInt(command[1]);r = Integer.parseInt(command[2]);Reverse(++l, ++r);} else {l = Integer.parseInt(command[1]);r = Integer.parseInt(command[2]);val = Integer.parseInt(command[3]);Revolve(++l, ++r, val);}}return output;}public Poj3580() {for (int i = 0; i < tr.length; i++) {tr[i] = new node();}}void Update(int x) {tr[x].minv = tr[x].val;tr[x].size = 1;if (tr[x].son[0] > 0) {tr[x].size += tr[tr[x].son[0]].size;tr[x].minv = Math.min(tr[x].minv, tr[tr[x].son[0]].minv);}if (tr[x].son[1] > 0) {tr[x].size += tr[tr[x].son[1]].size;tr[x].minv = Math.min(tr[x].minv, tr[tr[x].son[1]].minv);}}void Pushdown(int x) {if (tr[x].rev == 1) { // 下传翻转标记tr[x].rev ^= 1;int temp = tr[x].son[0];tr[x].son[0] = tr[x].son[1];tr[x].son[1] = temp;if (tr[x].son[0] > 0)tr[tr[x].son[0]].rev ^= 1;if (tr[x].son[1] > 0)tr[tr[x].son[1]].rev ^= 1;}if (tr[x].add == 1) { // 下传加标记if (tr[x].son[0] > 0) {tr[tr[x].son[0]].add += tr[x].add;tr[tr[x].son[0]].val += tr[x].add;tr[tr[x].son[0]].minv += tr[x].add;}if (tr[x].son[1] > 0) {tr[tr[x].son[1]].add += tr[x].add;tr[tr[x].son[1]].val += tr[x].add;tr[tr[x].son[1]].minv += tr[x].add;}tr[x].add = 0;//清除标记}}// 生成新结点int New(int father, int val) {tr[++cnt].fa = father;tr[cnt].val = val;tr[cnt].minv = val;tr[cnt].size = 1;tr[cnt].add = tr[cnt].rev = 0;tr[cnt].son[0] = tr[cnt].son[1] = 0;return cnt;}// 旋转void Rotate(int x) {Pushdown(x);int y = tr[x].fa, z = tr[y].fa;int c = (tr[y].son[0] == x) ? 1 : 0;tr[y].son[1 - c] = tr[x].son[c];tr[tr[x].son[c]].fa = y;tr[x].fa = z;if (z > 0)tr[z].son[tr[z].son[1] == y ? 1 : 0] = x;tr[x].son[c] = y;tr[y].fa = x;Update(y);Update(x);}// 将 x 旋转为 goal 的儿子void Splay(int x, int goal) {while (tr[x].fa != goal) {int y = tr[x].fa, z = tr[y].fa;if (z != goal) {if (((tr[z].son[0] == y ? 1 : 0) ^ (tr[y].son[0] == x ? 1 : 0)) == 0) {Rotate(y);} else {Rotate(x);}}Rotate(x);}// 如果 goal 是 0，则更新根为 xif (goal == 0) root = x;}int Findk(int x, int k) {while (true) {Pushdown(x);int sn = tr[x].son[0] > 0 ? tr[tr[x].son[0]].size + 1 : 1;if (k == sn)return x;if (k > sn) {k -= sn;x = tr[x].son[1];} elsex = tr[x].son[0];}}// 插入值 valvoid Insert(int pos, int val) {int x = Findk(root, pos), y = Findk(root, pos + 1);Splay(x, 0);Splay(y, x);tr[y].son[0] = New(y, val);Update(y);Update(x);}// 删除void Delete(int pos) {int x = Findk(root, pos - 1), y = Findk(root, pos + 1);Splay(x, 0);Splay(y, x);tr[y].son[0] = 0;Update(y);Update(x);}// 找 [l,r] 区间最小值int Min(int l, int r) {int x = Findk(root, l - 1), y = Findk(root, r + 1);Splay(x, 0);Splay(y, x);return tr[tr[y].son[0]].minv;}int Build(int l, int r, int t, int fa) {if (l > r)return t;int mid = l + r >> 1;t = New(fa, a[mid]);tr[t].son[0] = Build(l, mid - 1, tr[t].son[0], t);tr[t].son[1] = Build(mid + 1, r, tr[t].son[1], t);Update(t);return t;}void Init() {cnt = root = 0;tr[0].son[0] = tr[0].son[1] = 0;root = New(0, -inf); // 创建虚结点1tr[root].son[1] = New(root, inf); // 创建虚结点2tr[root].size = 2;tr[tr[root].son[1]].son[0] = Build(1, n, tr[tr[root].son[1]].son[0], tr[root].son[1]);Update(tr[root].son[1]);Update(root);}// [l,r] 区间加上 valvoid Add(int l, int r, int val) {int x = Findk(root, l - 1), y = Findk(root, r + 1);Splay(x, 0);Splay(y, x);tr[tr[y].son[0]].val += val;tr[tr[y].son[0]].minv += val;tr[tr[y].son[0]].add += val;Update(y);Update(x);}// [l,r] 区间翻转void Reverse(int l, int r) {int x = Findk(root, l - 1), y = Findk(root, r + 1);Splay(x, 0);Splay(y, x);tr[tr[y].son[0]].rev ^= 1; // 加翻转标记}// 偏移 T 位void Revolve(int l, int r, int T) {T %= r - l + 1;if (T == 0) return;int x = Findk(root, r - T), y = Findk(root, r + 1);Splay(x, 0);Splay(y, x);int tmp = tr[y].son[0];tr[y].son[0] = 0;Update(y);Update(x);x = Findk(root, l - 1);y = Findk(root, l);Splay(x, 0);Splay(y, x);tr[y].son[0] = tmp;tr[tmp].fa = y;Update(y);Update(x);}
}class node {int son[] = new int[2];//左右孩子0,1int val, fa; // 值，父亲int minv; // 最小值int size, add, rev; // 大小，加标记，翻转标记
}

超级记忆节目

一问题描述

二输入

三输出