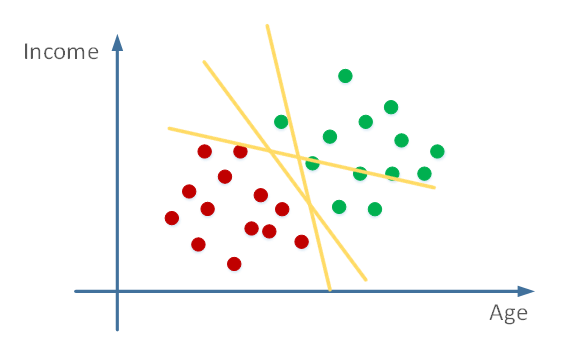
数理统计期末复习笔记

主要内容：
数据压缩，点估计，假设检验，区间检验

Reference: Statistical Inference, Casella&Berger

Chapter 6 Data Reduction（数据压缩）

随机样本：

• 无限样本：$X_1,...,X_n\stackrel{iid}{\sim }f(x|\theta ),f(\vec{x}|\theta )={\prod }_{i=1}^{n}f(x_i|\theta )$

• 有限样本：有放回：仍为独立同分布；无放回：边缘分布相同

统计量：

• 关于样本$X_1,...,X_n$的函数$T(X_1,...,X_n)$：用来重定向参数$\theta$的若干性质
• eg：样本均值：$\overline{X}=\frac{X_1+....+X_n}{n}$，样本方差：$S^2=\frac{{\sum }_{i=1}^n(X_i-\overline{X}{)}^2}{n-1}$，分母为n-1是因为此时是${\sigma }^2$的无偏估计

充分统计量：

• 统计量$T(X_1,...,X_n)$是充分统计量当且仅当$P(x_1,...,x_n|T(x_1,...,x_n)=t,\theta )=P(x_1,...,x_n|T(x_1,...,x_n)=t)$

• 本质：将$(X_1,...,X_n)$的空间根据$T$的值作划分

• 判定：$T(X_1,...,X_n)$是充分统计量当且仅当存在函数$g,h:p(x_1,...,x_n|\theta )=h(x_1,...,x_n)g(T(x_1,...,x_n)|\theta )$（密度函数分离）

最小充分统计量：

• 统计量$T(X_1,...,X_n)$是最小充分统计量当且仅当其为充分统计量，且任意充分统计量$U$，$T=g(U)$

• 本质：$T$的值决定空间的最大可能分划

• 判定：$T(X_1,...,X_n)$是最小充分统计量当且仅当仅当$R(x,y|\theta )=\frac{p(y_1,...,y_n|\theta )}{p(x_1,...,x_n|\theta )}$当且仅当$T(x)=T(y)$时与$\theta$独立

完全统计量：

• 对于分布族$p(x_1,...,x_n|\theta ),\theta \in \Theta$，统计量$T(X_1,...,X_n)$是完全统计量当且仅当对任意$g$，若$E_{\theta }(g(T))=0,\forall \theta$，则$g=0a.e.$ 注：$E_\theta f(x,\theta)=\int f(x,\theta) p(x|\theta)dx $

• 判定：

  • 是：证明$\int g(T(x_1,...,x_n))p(x_1,...,x_n|\theta )=0\Rightarrow g=0a.e.$
  • 否：构造函数$g\ne 0$，但是$E_{\theta }g(T)=0,\forall \theta$；一般来说定义域与$\theta$相关的函数没有完全充分统计量

• 性质：完全统计量必定是充分统计量；完全统计量和最小充分统计量无关；但是在指数组分布中，完全统计量必定是最小充分统计量

辅助统计量：

• 统计量$S(x_1,...,x_n)$是辅助统计量当且仅当$S$与$\theta$独立
• 性质：Basu定理：任何完全统计量和辅助统计量独立

Chapter 7 Point Estimation（点估计）

估计：给定采样$X_1,...,X_n$，利用其估计参数$\theta$

矩估计

对$\theta =({\theta }_1,...,{\theta }_k)$，求解方程组：
$$\{\begin{array}{rl}& {\mu }_1(\theta )=E(X)=\frac{X_1+...+X_n}{n}\\ & {\mu }_2(\theta )=E(X^2)=\frac{X_1^2+...+X_n^2}{n}\\ & ...\\ & {\mu }_k(\theta )=E(X^k)=\frac{X_1^k+...+X_n^k}{n}\end{array}$$
得到对$({\theta }_1,...,{\theta }_k)$的矩估计$({\hat{\theta }}_1,...,{\hat{\theta }}_k)$.

优点：计算方便

缺点：渐近性质不好，结果可能在定义域${\Theta }_k$以外

极大似然估计

基本概念：

• 似然函数：$L(\theta |x)=p(x_1,...,x_n|\theta )={\prod }_{i=1}^{n}p(x_i|\theta )$；对数似然函数：$I(\theta |x)=\log p(x_1,...,x_n|\theta )={\sum }_{i=1}^n\log p(x_i|\theta )$

• 定义：$\hat{\theta }={\mathrm{argmax}}_{\theta \in \Theta }L(\theta |x)$

验证：

• 必要条件：$\frac{\partial L}{\partial \theta }=0,\frac{\partial L}{\partial {\theta }^2}⪯0$ semi negative definite并且小于等于函数的边界值
• 证明：$c\ge I(\theta |x)$并且取等当且仅当$\theta =\hat{\theta }$
• 在离散参数中间中，可以计算相邻比值$L(k+1|x)/L(k|x)$判断大小

性质：

• 不变性：如果$\theta$的最大似然估计是$\hat{\theta }$，那么$\mu =g(\theta )$的最大似然估计就是$\hat{\mu }=g(\hat{\theta })$

• 对于$\theta$的任意估计$W(x_1,...,x_n)$，如果$\frac{\partial }{\partial \theta }{E}_{\theta }W(x)=\int W(x)\frac{\partial }{\partial \theta }f(x|\theta )dx$

  • $$Var(W(x))\ge \frac{(\frac{\partial }{\partial \theta }{E}_{\theta }W(x){)}^2}{E_{\theta }((\frac{\partial }{\partial \theta }\log f(x|\theta ){)}^2)}$$

    分母$=n{E}_{\theta }((\frac{\partial }{\partial \theta }\log p(x|\theta ){)}^2)$=Fisher Information

    • Fisher Information Matrix ${\mathcal{I}}_n(\theta )$：描述$X$为刻画$\theta$带来的信息量大小的矩阵；当$\theta$为k维时是$k\times k$的矩阵，这里的分母是1维的情况：

    $$[{\mathcal{I}}_n(\theta ){]}_{i,j}={\mathrm{E}}_{\theta }\left[\left(\frac{\partial }{\partial {\theta }_i}\log f(X;\theta )\right)\left(\frac{\partial }{\partial {\theta }_j}\log f(X;\theta )\right)\right]$$

    • 特别的，如果$W$无偏，则$Var(W)\ge \frac{1}{n{E}_{\theta }((\frac{\partial }{\partial \theta }\log p(x|\theta ){)}^2)}$为定值

    • 对于指数组分布，有$\frac{\partial }{\partial \theta }{E}_{\theta }(\frac{\partial }{\partial \theta }\log p(x|\theta )=\int \frac{\partial }{\partial \theta }(\frac{\partial }{\partial \theta }\log p(x|\theta )p(x|\theta ))dx$，从而
      $$E_{\theta }((\frac{\partial }{\partial \theta }\log p(x|\theta ){)}^2=-E_{\theta }(\frac{{\partial }^2}{\partial {\theta }^2}\log p(x|\theta ))$$
      ，以及：${\mathcal{I}}_n(\theta )=-E(\frac{{\partial }^{2}I(\theta )}{\partial {\theta }_r\partial {\theta }_s})$

    • $MSE=E_{\theta }(\hat{\theta }-\theta {)}^2=B^2+V$: $V=Va{r}_{\theta }(\hat{\theta }),B=E_{\theta }(\hat{\theta })-\theta$

      因此，在偏差$B$和方差$V$之间必然有tradeoff

渐近性：

• 正规化条件：

  • 分布$P_{\theta }$有共同的支集
  • 参数空间$\Theta$包含一个${\mathbb{R}}^k$中的开集
  • $\hat{\theta }$是唯一使得$\frac{\partial }{\partial \theta }I(\theta |x)=0$的$\theta$

• 一致性：$\theta \stackrel{p}{\to }{\theta }_0$

• 渐近正态性：$\sqrt{n}(\hat{\theta }-{\theta }_0)\stackrel{d}{\to }N(0,\frac{1}{I(\theta )})$，$I(\theta )$就是$\frac{{\mathcal{I}}_n(\theta )}{n}$，即$E_{\theta }((\frac{\partial }{\partial \theta }\log p(x|\theta ){)}^2)$，所以也可以写成$(\hat{\theta }-{\theta }_0)\stackrel{d}{\to }N(0,\frac{1}{I_n(\theta )})$

  推论：(Delta Method)$\sqrt{n}(\gamma (\hat{\theta })-\gamma ({\theta }_0))\stackrel{d}{\to }N(0,\frac{{\gamma }^{\prime }(\theta {)}^2}{I(\theta )})$

• 渐近有效性：样本数量充分大时，$\hat{\theta }$是无偏估计中方差最小的

Best Unbiased Estimator最佳无偏估计

对于$t(\theta )$的估计$W$，如果$\forall \theta ,E_{\theta }W=t(\theta )$，则称其无偏；如果$W$无偏，且对任意其它无偏估计$W^{\prime }$，$Va{r}_{\theta }(W^{\prime })\ge Va{r}_{\theta }(W),\forall \theta$，则称$W$为最佳无偏估计量

性质：

最佳无偏估计量不一定存在，但是若存在则唯一

判定：

• $W$是最佳无偏估计当且仅当其与任意其它无偏估计不相关：$cor(W,W^{\prime })=0$

• 证明$W$不是最佳无偏估计：给出一个和$W$相关的无偏估计

• 给出一个无偏估计：取$X$的一个完全统计量$T$，则：

  • $T$的任意一个函数$\varphi (T)$都是$E_{\theta }\varphi (T)$的无偏估计
  • 任意$h(x_1,...,x_n)$若为$t(\theta )$的一个无偏估计，则$\varphi (T)=E(h(x_1,...,x_n)|T)$是$t(\theta )$的无偏估计

Chapter 7 假设检验

基本定义

• 通过样本反推参数$\theta$是否满足属于某个集合${\Theta }_0$：

  零假设$H_0$：$\theta \in {\theta }_0$；否则：$H_1$: $\theta \in {\Theta }_1=\Theta /{\Theta }_0$. 设定一个判定规则：输入$X$，输出接收/拒绝

  如果样本X是由$\theta \in {\Theta }_0$生成的，则本应接收。如果拒绝了，则造成第一类错误（假阳性）

  如果样本X是由$\theta \in {\Theta }_1$生成的，则本应拒绝。如果接收了，则造成第二类错误（假阴性）

• 假设判定规则定义了拒绝区域$R$，拒绝$H_0$当且仅当$T(X)\in R$，则：

  权函数$\beta (\theta )=P_{\theta }(T(X)\in R)$，当$\theta \in {\Theta }_0$时，$\beta (\theta )=P_{\theta }(第一类错误率)$；否则=$1-P_{\theta }(第二类错误率)$

  • 目标：尽可能减少这两类错误的概率，即在${\Theta }_0$中$\beta$尽可能，${\Theta }_1$中$\beta$尽可能大

  • 但是一般来说根据连续性两个目标不太可能同时达到，所以改为定义检验水平（固定一端）：

    如果${\sup }_{\theta \in {\Theta }_0}\beta (\theta )=\alpha$，则称为size为$\alpha$的检验；如果$\le \alpha$，则称为level为$\alpha$的检验

    如果${\sup }_{\theta \in {\Theta }_0}\beta (\theta )\le {\inf }_{\theta \in {\Theta }_1}\beta (\theta )$，则称为无偏的检验

常见的检验构造方法

似然比方法

• 定义$\lambda (x)=\frac{{\sup }_{\theta \in {\Theta }_0}L(\theta |x)}{{\sup }_{\theta \in \Theta }L(\theta |x)}=\frac{L(\widehat{{\theta }_0}|x)}{L(\hat{\theta }|x)}$，当$\lambda (x)\le c$时拒绝

  注：$\lambda$也可考虑直接取关于充分统计量$T$的函数

  优势：最普适的构造方法；可以用来消去讨厌参数（nuisance parameter，即不需要检验但是与分布有关的参数）

• 渐近性：

  假设$x_1,...,x_n\stackrel{iid}{\sim }f(x|\theta )$，则在零假设下，$-2\log \lambda (x)\stackrel{d}{\to }{\chi }_k^2,k=\dim (\Theta )-\dim ({\Theta }_0)$

  从而，如果建立一个检验，在$-2\log \lambda (x)\ge {\chi }_{k,\alpha }^2$时拒绝，则得到一个渐近level为$\alpha$的检验

一致最大功效检验（UMP）

• 假设$C_{\alpha }$是所有level为$\alpha$的检验的集合，则对任意$\beta ()\in C_{\alpha }$，$\beta$是UMP当且仅当任意其它${\beta }^{\prime }\in C_{\alpha }$，${\beta }^{\prime }(\theta )\le \beta (\theta ),\forall \theta \in {\Theta }_0^c$

• 判定：

  • 如果Θ0={θ0},Θ1={θ1}\Theta_0=\{\theta_0\},\Theta_1=\{\theta_1\}Θ0​={θ0​},Θ1​={θ1​}，那么一个具有拒绝区域R={x∣f(x∣θ1)>kf(x∣θ0)}R=\{x|f(x|\theta_1)>kf(x|\theta_0)\}R={x∣f(x∣θ1​)>kf(x∣θ0​)}，并且$P_{{\theta }_0}(x\in R)=\alpha$的测试必定是一个UMP检验

  • 如果Θ0={θ≤θ0},Θ1={θ>θ0}\Theta_0=\{\theta\leq \theta_0\},\Theta_1=\{\theta>\theta_0\}Θ0​={θ≤θ0​},Θ1​={θ>θ0​}，并且分布族$P_{\theta }$是单调的：$\forall {\theta }_1<{\theta }_2$，$\frac{f_{{\theta }_2}(x)}{f_{{\theta }_1}(x)}$在区域{x∣fθ2(x)>0或fθ1(x)>0}\{x|f_{\theta_2}(x)>0 或f_{\theta_1}(x)>0\}{x∣fθ2​​(x)>0或fθ1​​(x)>0}上单调不减，那么一个当且仅当$T(x)>t_0$时拒绝的检测是level为$\alpha =P_{{\theta }_0}(T>t_0)$的UMP检验

• 注意：

  对于离散的分布，UMP可能是离散的

  UMP检测不一定存在

Wald检验和Score检验

• 这两个检验方法是渐近性的
• 如果Θ0={θ0}\Theta_0=\{\theta_0\}Θ0​={θ0​}，则在零假设下，有$\sqrt{\mathcal{I}(\theta )}(\hat{\theta }-\theta )\stackrel{asy}{\to }N(0,1)$（$\hat{\theta }$为MLE），并且在一般情况下$\mathcal{I}(\theta )\to Var(\theta )$，因此，得到两个自然的渐近检验：
  • Wald：$\left|\frac{\hat{\theta }-\theta }{\sqrt{Var(\hat{\theta })}}\right|\ge Z_{\alpha /2}$，其中$Var(\hat{\theta })$可以通过分布求出
  • Score：$\left|\frac{\hat{\theta }-\theta }{\sqrt{Var(\theta )}}\right|\ge Z_{\alpha /2}$，其中$Var(\theta )$可以通过分布求出

Union Intersection和Intersection Union检验：

• 这两个检验是为了解决假设是某些简单集合的并集的情况。这里前一个项是指拒绝域的形式，后一个项是指零假设的形式
• 因此：${\Theta }_0={\cap }_{\gamma \in \Gamma }{\Theta }_{\gamma }$，则为Union Intersection检验。将其分解为若干检验$H_{\gamma }$：$H_{\gamma 0}={\Theta }_{\gamma }$，假设每个检验的拒绝域为$R_{\gamma }$，则最终得到的检验的拒绝域$R={\cup }_{\gamma \in \Gamma }{R}_r$，因为接受域小，所以拒绝域相对的就大
• 反之，${\Theta }_0={\cup }_{\gamma \in \Gamma }{\Theta }_{\gamma }$，则为Intersection Union检验。将其分解为若干检验$H_{\gamma }$：$H_{\gamma 0}={\Theta }_{\gamma }$，假设每个检验的拒绝域为$R_{\gamma }$，则最终得到的检验的拒绝域$R={\cap }_{\gamma \in \Gamma }{R}_r$，

p值

• p值是一个关于样本的函数$p(x)$，表征的是$H_0$为真时观测到至少与当前样本$x$相同极端的样本的概率。也就是说，如果一个样本的p值为$t$，则可以断言同类型样本的出现概率为t

• 一般使用p值都是反过来用，即把要验证的假设当做$H_1$，然后说明样本具有足够小的p值（一般取0.05），从而说明如果$H_0$成立，那么样本会是非常特殊的，从而反过来证明$H_1$很可能成立

• 依据上面的性质，可以抽象出一个定义：

  $0\le p(x)\le 1,\forall x$. 一个p值是有效的，当且仅当对任意$\theta \in {\Theta }_0,\forall \alpha$，$P_{\theta }(x:p(x)\le \alpha )\le \alpha$，也就是说，在${\Theta }_0$中，小的p值一定意味着小的出现概率，进一步意味着$H_1$为真。

• 构造：考虑构造函数$W(x)$：较大的$W$值意味着$H_1$更可能为真

  对任意$x$，定义$P(x)={\sup }_{\theta \in {\Theta }_0}{P}_{\theta }(W(X)\ge W(x))$即为所求p值

置换检验

$X_1,...,X_n\sim F,Y_1,...,Y_m\sim G$，现在希望检验$H_0:F=G,H_1:F\ne G$

定义$T=|{\overline{X}}_n-{\overline{Y}}_m|$，对$X_1,...,Y_m$做置换，得到$T$值$T_i,i=1\sim N!$；并且原本的$T$值为$T_{obs}$，那么对于观测X的p值就是$P_0(T>T_{obs})=\frac{{\sum }_{i}1(T_i>obs)}{N!}$，因为理论上如果两个的分布相同那么p值应该会比较高。

Chapter 8 区间检验

置信区间：对于样本$x$，和区间$[L(x),U(x)]$，其置信度为$1-\alpha ={\inf }_{\theta }{P}_{\theta }(\theta \in [L(x),U(x)])$，也就是说，$\theta$至多只有$\alpha$的概率不在该区间中

构造：

• 概率不等式：

  Hoeffding’s不等式： $X_i\in [a_i,b_i]$ 独立，则P(∣X‾−EX∣≥t)≤2exp⁡{−2n2t2∑i(bi−ai)2}P(|\overline{X}-EX|\geq t)\leq 2\exp \{-\frac{2n^2t^2}{\sum_i(b_i-a_i)^2}\}P(∣X−EX∣≥t)≤2exp{−∑i​(bi​−ai​)22n2t2​}

• 测试取逆

  假设可以建立一个level为$\alpha$的测试，并且定义C(x)={θ0:x∈A(θ0)}C(x)=\{\theta_0:x\in A(\theta_0)\}C(x)={θ0​:x∈A(θ0​)}，则$C(x)$为一个$1-\alpha$的置信集合

• 枢轴方法

  $Q(X_1,...,X_n,\theta )$称为一个枢轴，若$Q$与$\theta$独立；则$P_{\theta }(a\le Q(x,\theta )\le b)=1-\alpha$（a,b为Q的分布的1-alpha区间端点）

• Delta方法（近似）

  $\hat{\theta }$为MLE，则由于$\sqrt{n}(\gamma (\hat{\theta })-\gamma ({\theta }_0))\stackrel{d}{\to }N(0,\frac{{\gamma }^{\prime }(\theta {)}^2}{I(\theta )})$，我们知道$\gamma ({\theta }_0)\pm Z_{1-\alpha /2}|{\pi }^{\prime }(\theta )|/\sqrt{I_n(\theta )}$（仔细推一下这个形式）

  高维情况：$\sqrt{n}\left(Y_n-\theta \right)\stackrel{d}{\to }{N}_p(0,\Sigma )$；$\sqrt{n}\left(g\left(Y_n\right)-g(\theta )\right)\stackrel{d}{\to }N\left(0,{\left(\frac{\partial g(\theta )}{\partial \theta }\right)}^{\prime }\Sigma \left(\frac{\partial g(\theta )}{\partial \theta }\right)\right)$

  $\Sigma$：协方差矩阵

• Score方法（近似）

  $Q(X\mid \theta )=\frac{\frac{\partial }{\partial \theta }\log L(\theta \mid X)}{\sqrt{-E_{\theta }\left(\frac{{\partial }^2}{\partial {\theta }^2}I(\theta \mid X)\right)}}\to N(0,1)$，因此集合$\left\{\theta :|Q(x\mid \theta )|\le z_{\alpha /2}\right\}$置信区间为$1-\alpha$

• LRT方法（近似）

  同理，当${\Theta }_0={\theta }_0$时，LRT的渐进性也可以用来构造置信区间：$C_n=\left\{\theta :\frac{L(\theta )}{L(\hat{\theta })}>e^{-{\chi }_{k,1-\alpha }^2/2}\right\}$

• 最优长度：在所有$1-\alpha$的置信区间中，存在某个长度最短的置信区间。这要求${\int }_a^{b}f(z)dz=1-\alpha$，当f单峰时把峰取在其中并且使得两端的函数值相等即可