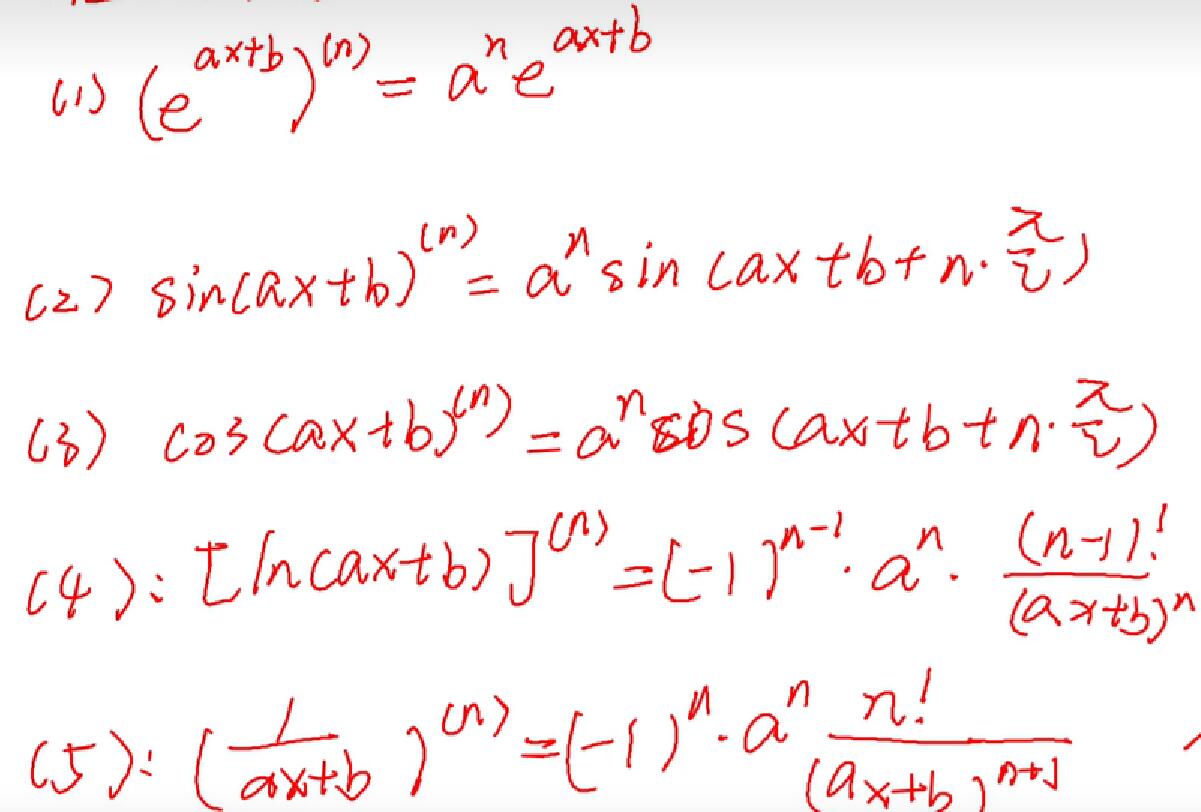一.极限
1.函数的四性:
单调性、周期性、奇偶性、有界性:
周期性、奇偶性各记住一个结论。
有界性判定:
- 1.定义法:-M<绝对值<M
- 2.函数性质:函数在闭区间上连续一定有界
闭区间连续===》开区间连续加左端点右极限和右端点左极限存在
- 3.局部有界性:在趋近某点极限存在,则在该点的去心领域内有界。
- 4.有界函数的四则运算(不包括除)结果有界。
2.极限性质
保号性:看语雀
使用范围:判断函数或极限的正负性
数列的极限为a当且仅当数列的子数列极限也为a。
3.求极限

判断类型,无论是什么都化成0*0和∞*∞型。
其中某次化简结果为f(x)/xn ,这是典型的泰勒公式,展开到和分母同样的阶次即可求出结果。
4.无穷小定阶
5.间断点
第一类间断点:
- 可去间断点:无定义或极限与函数值不相等===》左右极限存在且相等
- 跳跃间断点:左右极限存在但不相等
第二类间断点:
- 左右极限至少有一个不存在
6.证明题
- 1.零点定理
- 2.介值定理
- 3.最值定理
- 4.有界定理
7.数列极限
- 放缩+夹逼准则
- 定积分定义
- 单调有界准则
数列极限无论什么方法都要用到放缩
二.一元函数微分
1.导数与微分的概念
lim @ x → 0 f ( x + @ x ) − f ( x ) @ x \lim_{@x\rightarrow0}\frac{f(x+@x)-f(x)}{@x} lim@x→0@xf(x+@x)−f(x)
lim x → 0 f ( x ) − f ( 0 ) x \lim_{x\rightarrow0}\frac{f(x)-f(0)}{x} limx→0xf(x)−f(0)
这两种导数的极限表达式一定要掌握
函数在某点连续:该点左右极限存在且相等
函数在某点可导:该店左右导数存在且相等(此处一般用极限式定义求导数)
2.导数与微分的计算
参数方程求导:
一阶导= d y / d t d x / d t \frac{dy/dt}{dx/dt} dx/dtdy/dt
二阶导= d ( 一阶导 ) / d t d x / d t \frac{d(一阶导)/dt}{dx/dt} dx/dtd(一阶导)/dt
隐函数求导:
方程两端同时对x求导
反函数求导:
一阶导:正向一阶导 的倒数
二阶导:- 正向 2 阶导 一阶导的三次方 \frac{正向2阶导}{一阶导的三次方} 一阶导的三次方正向2阶导
求高阶导:
1.求多项,数学归纳(找规律)
2.组合公式法,直接记忆:
所谓组合公式,就是你记住这五个常用,然后想办法变成这五种类型
3.泰勒级数展开:
根据常用的麦克劳林展开式列出泰勒级数(一项一项的写比较清楚,不要直接写求和式);
根据n阶导看x的指数,消去n-1项,即为所求的导数。
参考:参考视频
乘积求导:(一般x0 是某个函数的零点)
1.乘法法则:f(x)=t(x)*g(x)
这里取一个当x=x0 时,t(x)等于0的简化
2.导数的定义
这里指的是化为定义极限表达式求解更简单
3.莱布尼兹公式
复习记得看语雀。
3.导数的应用
1.法线===》切线(导数的几何应用)
2.曲率,曲率半径
k= 二阶导的绝对值 ( 1 + 一阶导的平方 ) 的 3 / 2 次方 \frac{二阶导的绝对值}{(1+一阶导的平方)的3/2次方} (1+一阶导的平方)的3/2次方二阶导的绝对值 R= 1 k \frac{1}{k} k1
3.物理应用
一般涉及复合函数求导
4.函数的单调性、极值、最值
驻点:一阶导=0加无定义(改变单调性)
拐点:二阶导=0加无定义(改变凹凸性)
一阶导=0 + 二阶导<0 ===》极大
一阶导=0 + 二阶导>0===》极小
找极值点,先找驻点与不可导点,然后判断;
找最值点,先找极值点和端点,然后比较判断。
5.曲线的凹凸性、拐点、渐近线
拐点
二阶导=0 + 三阶导>0 ===》左凸右凹
二阶导=0 + 三阶导<0 ===》左凹右凸
区间凹凸性:二阶导>=0===》区间凹;
二阶导<=0===》区间凸。
渐近线的求法:
1.水平渐近线:左、右无穷极限
2.铅直渐近线:无定义,特殊处理,观察
3.斜渐近线:a= lim x → + ∞ f ( x ) x \lim_{x\rightarrow+\infty}\frac{f(x)}{x} limx→+∞xf(x)
b= lim x → + ∞ ( f ( x ) − a x ) \lim_{x\rightarrow+\infty}(f(x)-ax) limx→+∞(f(x)−ax)
注意,求斜渐近线左右极限都要求
6.不等式的证明1
这一处的不等式主要是证明函数>=0的问题,或者两个函数比较什么的,反正就是最后要证明一个函数>0,
最主要用的就是单调性来判断符号,奇偶性缩减区间,就是利用函数的性质来证明。
7.方程根的存在性和个数
- 零点定理(一般函数不含导数)
- 罗尔定理(一般函数就包含导数)
- 拉格朗日中值定理
- 柯西中值定理
方程根的个数利用划分单调区间证明。
这里有时候会用到证明极限的存在:
极限存在的两个重要法则:1)夹逼定理;2)单调有界定理
罗尔定理:
- 1.找辅助函数
- 2.找相同的函数值(看存在几个根就找几组相同的函数值或者三个点处函数值相同)
补充一个点:
导函数的至少(至多)零点问题:
- 1.如果f(x)有k个零点,则一阶导函数至少有(k-1)个零点……(k-1)阶导函数至少有1个零点。
- 2.一阶导函数没有零点,所以原函数存在至多一个零点;同理,如果一阶导至多有一个零点,则原函数至多有两个零点,其他类推。
三.一元积分学
1.原函数的概念
- 有第一类间断点的函数不存在原函数(连续函数肯定存在,有间断点的判断是不是第一间断点)
- f(x)在[a,b]上可积的两个充分条件:
- f(x)在[a,b]上连续
- f(x)在[a,b]上有界且只有有限个间断点
注意:可积不等价于存在原函数
2.定积分的性质
常见有比较积分的大小,通过奇偶性计算积分等
注意比较积分的大小非常重要,参考语雀笔记15
这里注意可以通过f(x)的正负判断积分的正负,但不能用F(x)判断导函数的正负。
3.不定积分的计算
分部积分:反对幂指三(保留顺序)
不定积分换元时,结果要替换回原来的代换。
分段函数求积分,分段求,不规则函数记得写成分段函数。
有理函数积分:
1)分子次数比分母高,化为多项式加真分式
2)分母能分解,分解因式、裂项
3)分母不能分解,分子凑分母的微分,或特殊函数
4.定积分的计算
对称区间的定积分计算,不想说。
定积分的几何意义,以及求数列的极限(不要忘了)。
计算有关周期函数定积分常用到的结论:

这里有很多陷阱,注意规避。
5.变限积分
在考研范围内,你所遇到的几乎所有变限积分都会用到变限积分公式。
变限积分的使用:
- 1.直接作为x的原函数,讨论相关问题
- 2.求极限(洛必达)
- 3.求极限(中值定理)(少,但一定要会)
所以重点还是求极限。
重要结论:
若f(x)为[a,b]上的可积函数,F(x)= ∫ a x f ( t ) d t \int_a^xf(t)dt ∫axf(t)dt ,则F(x)连续且:
若f(x)连续,则F可导且F` (x)=f(x)。
若f不连续,则:1.f有可去间断点,F可导但间断点处F的导数不等于f
2.f有跳跃间断点,F在f的跳跃间断点不可导
6.反常积分
反常积分的计算通常包含瑕点(奇点)的问题,只要奇点在积分区间内,无论是端点还是中间,都要分段积分。
计算的都比较简单,主要是判断反常积分的审敛性。
通过积分计算判断反常积分的收敛是最基础的,下面才是提升。
无穷区间的反常积分的审敛:
- 比较判别法:记住参照函数(P积分)
无界函数的反常积分的审敛:
- 先找瑕点
- 判断瑕点极限(P积分,与上面不同)
不记得 就复习高图或者世纪高教都行。

7.定积分的应用
- 1.平面图形面积
- 2.平面曲线弧长
- 3.旋转体体积
- 4.旋转曲面面积
- 5.在区间平行某截面的立体体积
- 6.物理应用
- 7.没有公式,自己根据理解写出积分
定积分的应用公式键手写笔记。
8.积分综合
这里以世纪高教的例题为例:
-
1.积分与微分方程结合,求f(x)
-
2.积分的意义与极限结合,求极限
-
3.关于积分的证明题(重点)
四.多元微分学
1.偏导数与全微分的概念
遇到这种概念题,一般是选择题,直接代特例
可微的定义: lim x → 0 , y → 0 f ( x , y ) − f ( 0 , 0 ) − A x − B y x 2 + y 2 \lim_{x\rightarrow0,y\rightarrow0}\frac{f(x,y)-f(0,0)-Ax-By}{\sqrt{x^2+y^2}} limx→0,y→0x2+y2f(x,y)−f(0,0)−Ax−By=0则可微
这里的A、B分别表示f(x,y)关于x、y的偏导数
这里经常是极限存在、连续、(偏)导数存在、可微,关系递进。前面不满足后面一定不满足,后面满足前面一定满足。
详细请看语雀。
2.偏导数与全微分的计算
隐函数求偏导,公式记清楚。
先对x求导再对y求偏导 与 先对y求偏导再对x求偏导 结果相等
3.方程变换问题
所谓的变换就是利用中间变量求偏导的问题
4.极值与最值
求f(x,y)分别对x和y的一阶偏导,求驻点
A=F关于x求二阶偏导,B=F关于x求偏导后再对y求偏导,C=F关于y求二阶偏导
AC-B2 >0时才有极值,A>0极小,A<0极大。
AC-B2 <0时,没有极值
AC-B2 =0时,进一步讨论。
有时候他给的是一个方程不是具体函数,使用隐函数求导法则
5.条件极值问题
重点掌握:拉格朗日乘数法
条件极值多是应用题环境
五.二重积分
1.二重积分的概念与性质
二重积分的定义与几何意义;
这一部分常考的题是多个函数在同一区间上积分的大小,或者一个函数在不同区间的正负性。
性质:
- 1.比较定理
- 2.估值定理
- 3.中值定理
2.二重积分的计算
个人计算步骤总结:
- 1.画图,积分区域
- 2.判断极坐标适用性
- 3.考虑积分性质
- 4.想其他办法
- 被积函数是1,结果是积分区域D的面积;
- 被积函数是0,不用看区间了,结果就是0。
重点:函数的奇偶性是重点。
3.坐标系的选择
一般积分区域含有圆域,并且被积函数含有典型的x2 + y2 .
这里可能会用到华力士公式(以0为底)或者三角代换(不以0为底)
4.乱换对称性
质心计算公式:看语雀
轮换=两者相加/2;
奇函数(* | /)奇函数 = 偶函数;
奇函数 * | /)偶函数 = 奇函数;
口诀“同偶异奇”
5.交换积分次序
我们在一元积分的时候,求积分时的几何意义是面积,而且在x轴上方是正的,在其下方是负的。
但是在这里的二重积分,你画的积分区域,就没有这种意思,二重积分它是空间立体的体积,没有一重积分的说法。而且相较一元积分学,他往往会考虑函数与积分区间的性质。
6.区域分块
此时一般积分区域未知,或很难画出来
看这里重点复习世纪高教摆线区域的题。
7.二重积分的综合应用
抽象函数求二重积分。
六.常微分方程
1.一阶微分方程
- 1.可分离变量的微分方程
- 2.齐次方程
- 3.线性方程
- 4.全微分方程
2.可降阶的高阶微分方程
- 1.不显含y
- 2.不显含x
3.线性常系数微分方程
- 1.二阶常系数齐次微分方程(3种解,看表)
- 2.二阶常系数非齐次微分方程(两种,复习)
4.解的结构相关问题
掌握结构定理,这里是重点
5.微分方程的综合应用
- 1.与积分或微分结合,求函数(重点是反常积分的结合)
- 2.实际应用,自己根据题意写微分方程
七.无穷级数
1.常数项基数审收敛
级数的性质。
必要条件是无穷远处趋于0.
常用的审敛法则:
- 1.含有n!====》用比值法
- 2.含有an 或nn ====》用根值法
- 3.抽象或等价无穷小好找====》比较判别法
- 4.都不行、极限审敛法
- 5.再不行,构造基准级数进行比较判别法
这里的证明题很重要。
2.幂级数的概念
- 幂级数概念
- 阿贝尔定理
- 收敛域
- 缺项幂级数的收敛半径
3.幂级数的和函数
章节重点
4.幂级数的展开式
章节重点
八.多元函数积分学
1.三重积分
前提:完全或基本掌握了二重积分的相关问题

这里注意,画图形区域的时候x2 + y2 =s 才是柱面,而x2 + y2 =z2 是个锥面。
2.第一类曲线积分
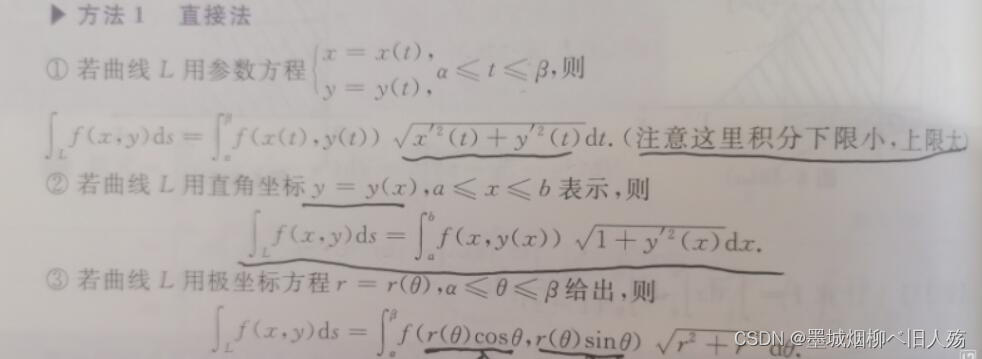
第一步永远是观察奇偶性和对称性
3.第二类曲线积分
第二类曲线积分与第一类曲线积分的转换
- 1.直接法
- 2.格林公式
- 3.补线用格林公式
- 4.线积分与路径无关
- 5.斯托克斯公式
4.第一类曲面积分
直接法,求在xoy面的投影域D,然后按公式计算。
5.第二类曲面积分
- 直接法,分三项二重积分计算,或者求偏导一次化为多个一重积分计算
- 高斯公式
- 不面用高斯公式
九.空间几何与场论初步
- 1.向量运算
- 2.平面与直线的关系
- 3.求空间曲面与空间曲线
- 4.方向导数
- 5.梯度、散度、旋度