一、GraphX介绍

        Spark GraphX是一个分布式图处理框架，它是基于Spark平台提供对图计算和图挖掘简洁易用的而丰富的接口，极大的方便了对分布式图处理的需求。
众所周知，社交网络中人与人之间有很多关系链，例如Twitter、Facebook、微博和微信等，这些都是大数据产生的地方都需要图计算，现在的图处理基本都是分布式的图处理，而并非单机处理。Spark GraphX由于底层是基于Spark来处理的，所以天然就是一个分布式的图处理系统。

        图的分布式或者并行处理其实是把图拆分成很多的子图，然后分别对这些子图进行计算，计算的时候可以分别迭代进行分阶段的计算，即对图进行并行计算。

二、GraphX框架

        设计GraphX时，点分割和GAS都已成熟，在设计和编码中针对它们进行了优化，并在功能和性能之间寻找最佳的平衡点。如同Spark本身，每个子模块都有一个核心抽象。GraphX的核心抽象是Resilient Distributed Property Graph，一种点和边都带属性的有向多重图。它扩展了Spark RDD的抽象，有Table和Graph两种视图，而只需要一份物理存储。两种视图都有自己独有的操作符，从而获得了灵活操作和执行效率。

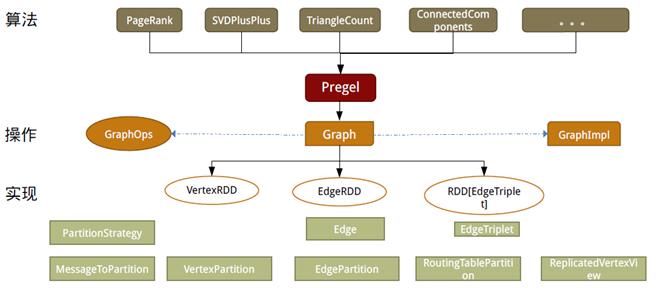
        如同Spark，GraphX的代码非常简洁。GraphX的核心代码只有3千多行，而在此之上实现的Pregel模式，只要短短的20多行。GraphX的代码结构整体下图所示，其中大部分的实现，都是围绕Partition的优化进行的。这在某种程度上说明了点分割的存储和相应的计算优化，的确是图计算框架的重点和难点。

三、GraphX术语

3.1 顶点和边

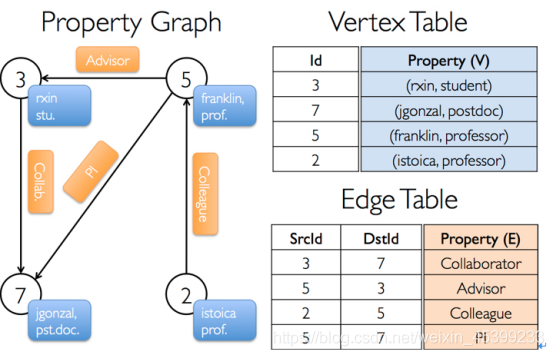
一般关系图中，事务为顶点，关系为边

3.2 有向图和无向图

在有向图中，一条边的两个顶点一般扮演者不同的角色，比如父子关系、页面A连接向页面B；

在一个无向图中，边没有方向，即关系都是对等的，比如qq中的好友。

GraphX中有一个重要概念，所有的边都有一个方向，那么图就是有向图，如果忽略边的方向，就是无向图。

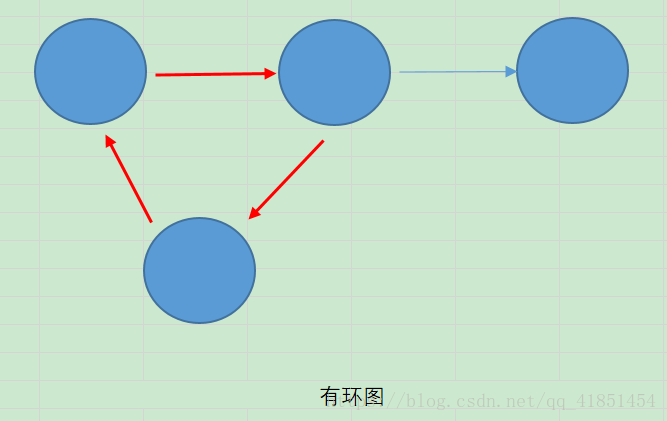
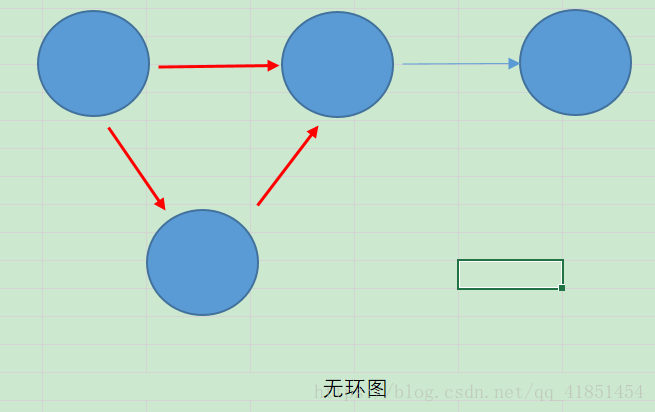
3.3 有环图和无环图

有环图是包含循环的，一系列顶点连接成一个环。无环图没有环。在有环图中，如果不关心终止条件，算法可能永远在环上执行，无法退出。

 

3.4、度、出边、入边、出度、入度

度表示一个顶点的所有边的数量

出边是指从当前顶点指向其他顶点的边

入边表示其他顶点指向当前顶点的边

出度是一个顶点出边的数量

入度是一个顶点入边的数量

3.5、超步

图进行迭代计算时，每一轮的迭代叫做一个超步

四、图处理技术

图处理技术包括图数据库、图数据查询、图数据分析和图数据可视化。

4.1 图数据库

Neo4j、Titan、OrientDB、DEX和InfiniteGraph等基于遍历算法的、实时的图数据库；

4.2 图数据查询

对图数据库中的内容进行查询

4.3 图数据分析

Google Pregel、Spark GraphX、GraphLab等图计算软件。传统的数据分析方法侧重于事物本身，即实体，例如银行交易、资产注册等等。而图数据不仅关注事物，还关注事物之间的联系。例如，如果在通话记录中发现张三曾打电话给李四，就可以将张三和李四关联起来，这种关联关系提供了与两者相关的有价值的信息，这样的信息是不可能仅从两者单纯的个体数据中获取的。

4.4　图数据可视化

OLTP风格的图数据库或者OLAP风格的图数据分析系统（或称为图计算软件），都可以应用图数据库可视化技术。需要注意的是，图可视化与关系数据可视化之间有很大的差异，关系数据可视化的目标是对数据取得直观的了解，而图数据可视化的目标在于对数据或算法进行调试。

五、图存储模式

在了解GraphX之前，需要先了解关于通用的分布式图计算框架的两个常见问题：图存储模式和图计算模式。

巨型图的存储总体上有边分割和点分割两种存储方式。2013年，GraphLab2.0将其存储方式由边分割变为点分割，在性能上取得重大提升，目前基本上被业界广泛接受并使用。

5.1 边分割（Edge-Cut）

　　每个顶点都存储一次，但有的边会被打断分到两台机器上。这样做的好处是节省存储空间；坏处是对图进行基于边的计算时，对于一条两个顶点被分到不同机器上的边来说，要跨机器通信传输数据，内网通信流量大。

5.2 点分割（Vertex-Cut）

　　每条边只存储一次，都只会出现在一台机器上。邻居多的点会被复制到多台机器上，增加了存储开销，同时会引发数据同步问题。好处是可以大幅减少内网通信量。

5.3　对比

　　虽然两种方法互有利弊，但现在是点分割占上风，各种分布式图计算框架都将自己底层的存储形式变成了点分割。主要原因有以下两个。

　　磁盘价格下降，存储空间不再是问题，而内网的通信资源没有突破性进展，集群计算时内网带宽是宝贵的，时间比磁盘更珍贵。这点就类似于常见的空间换时间的策略。

　　在当前的应用场景中，绝大多数网络都是“无尺度网络”，遵循幂律分布，不同点的邻居数量相差非常悬殊。而边分割会使那些多邻居的点所相连的边大多数被分到不同的机器上，这样的数据分布会使得内网带宽更加捉襟见肘，于是边分割存储方式被渐渐抛弃了。

六、GraphX中的pregel函数

6.1pregel函数源码 与 各个参数介绍：

　　Pregel借鉴MapReduce的思想，采用消息在点之间传递数据的方式，提出了“像顶点一样思考”（Think Like A Vertex）的图计算模式，采用消息在点之间传递数据的方式，让用户无需考虑并行分布式计算的细节，只需要实现一个顶点更新函数，让框架在遍历顶点时进行调用即可。

  def pregel[A: ClassTag](initialMsg: A,maxIterations: Int = Int.MaxValue,activeDirection: EdgeDirection = EdgeDirection.Either)(vprog: (VertexId, VD, A) => VD,sendMsg: EdgeTriplet[VD, ED] => Iterator[(VertexId, A)],mergeMsg: (A, A) => A): Graph[VD, ED] = {Pregel(graph, initialMsg, maxIterations, activeDirection)(vprog, sendMsg, mergeMsg)}

参数	说明
initialMsg	图初始化的时候，开始模型计算的时候，所有节点都会先收到一个消息
maxIterations	最大迭代次数
activeDirection	规定了发送消息的方向
vprog	节点调用该消息将聚合后的数据和本节点进行属性的合并
sendMsg	激活态的节点调用该方法发送消息
mergeMsg	如果一个节点接收到多条消息，先用mergeMsg 来将多条消息聚合成为一条消息，如果节点只收到一条消息，则不调用该函数

6.2 案例： 求顶点5 到 其他各顶点的 最短距离

在理解案例之前，首先要清楚关于 顶点 的两点知识：

1. 顶点 的状态有两种：
   (1)、钝化态【类似于休眠，不做任何事】
   (2)、激活态【干活】

2. 顶点 能够处于激活态需要有条件：
   (1)、成功收到消息 或者
   (2)、成功发送了任何一条消息

package com.hanwei.sparkgraphx01.helloworld
import org.apache.spark.{SparkConf, SparkContext}
import org.apache.spark.graphx._
import org.apache.spark.rdd.RDDobject Graphx06_Pregel extends App{//1、创建SparkContextval sparkConf = new SparkConf().setAppName("GraphxHelloWorld").setMaster("local[*]")val sparkContext = new SparkContext(sparkConf)//2、创建顶点val vertexArray = Array((1L, ("Alice", 28)),(2L, ("Bob", 27)),(3L, ("Charlie", 65)),(4L, ("David", 42)),(5L, ("Ed", 55)),(6L, ("Fran", 50)))val vertexRDD: RDD[(VertexId, (String,Int))] = sparkContext.makeRDD(vertexArray)//3、创建边，边的属性代表 相邻两个顶点之间的距离val edgeArray = Array(Edge(2L, 1L, 7),Edge(2L, 4L, 2),Edge(3L, 2L, 4),Edge(3L, 6L, 3),Edge(4L, 1L, 1),Edge(2L, 5L, 2),Edge(5L, 3L, 8),Edge(5L, 6L, 3))val edgeRDD: RDD[Edge[Int]] = sparkContext.makeRDD(edgeArray)//4、创建图（使用aply方式创建）val graph1 = Graph(vertexRDD, edgeRDD)/* ************************** 使用pregle算法计算 ，顶点5 到 各个顶点的最短距离 ************************** *///被计算的图中 起始顶点idval srcVertexId = 5L val initialGraph = graph1.mapVertices{case (vid,(name,age)) => if(vid==srcVertexId) 0.0 else Double.PositiveInfinity}//5、调用pregelval pregelGraph = initialGraph.pregel(Double.PositiveInfinity,Int.MaxValue,EdgeDirection.Out)((vid: VertexId, vd: Double, distMsg: Double) => {val minDist = math.min(vd, distMsg)println(s"顶点${vid}，属性${vd}，收到消息${distMsg}，合并后的属性${minDist}")minDist},(edgeTriplet: EdgeTriplet[Double,PartitionID]) => {if (edgeTriplet.srcAttr + edgeTriplet.attr < edgeTriplet.dstAttr) {println(s"顶点${edgeTriplet.srcId} 给 顶点${edgeTriplet.dstId} 发送消息 ${edgeTriplet.srcAttr + edgeTriplet.attr}")Iterator[(VertexId, Double)]((edgeTriplet.dstId, edgeTriplet.srcAttr + edgeTriplet.attr))} else {Iterator.empty}},(msg1: Double, msg2: Double) => math.min(msg1, msg2))//6、输出结果
//  pregelGraph.triplets.collect().foreach(println)
//  println(pregelGraph.vertices.collect.mkString("\n"))//7、关闭SparkContextsparkContext.stop()
}

输出结果：

//------------------------------------------ 各个顶点接受初始消息initialMsg ------------------------------------------
顶点3，属性Infinity，收到消息Infinity，合并后的属性Infinity
顶点2，属性Infinity，收到消息Infinity，合并后的属性Infinity
顶点4，属性Infinity，收到消息Infinity，合并后的属性Infinity
顶点6，属性Infinity，收到消息Infinity，合并后的属性Infinity
顶点1，属性Infinity，收到消息Infinity，合并后的属性Infinity
顶点5，属性0.0，收到消息Infinity，合并后的属性0.0
//------------------------------------------ 第一次迭代 ------------------------------------------
顶点5 给 顶点6 发送消息 3.0
顶点5 给 顶点3 发送消息 8.0
顶点3，属性Infinity，收到消息8.0，合并后的属性8.0
顶点6，属性Infinity，收到消息3.0，合并后的属性3.0
//------------------------------------------ 第二次迭代 ------------------------------------------
顶点3 给 顶点2 发送消息 12.0
顶点2，属性Infinity，收到消息12.0，合并后的属性12.0
//------------------------------------------ 第三次迭代 ------------------------------------------
顶点2 给 顶点4 发送消息 14.0
顶点2 给 顶点1 发送消息 19.0
顶点1，属性Infinity，收到消息19.0，合并后的属性19.0
顶点4，属性Infinity，收到消息14.0，合并后的属性14.0
//------------------------------------------ 第四次迭代 ------------------------------------------
顶点4 给 顶点1 发送消息 15.0
顶点1，属性19.0，收到消息15.0，合并后的属性15.0
//------------------------------------------ 第五次迭代不用发送消息 ------------------------------------------

6.3 pregel原理分析

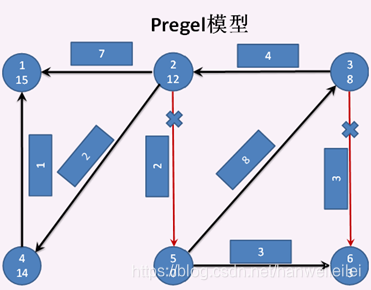
调用pregel方法之前，先把图的各个顶点的属性初始化为如下图所示：顶点5到自己的距离为0，所以设为0，其他顶点都设为 正无穷大Double.PositiveInfinity。

当调用pregel方法开始：
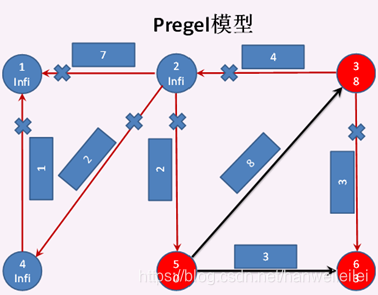
首先，所有顶点都将接收到一条初始消息initialMsg ，使所有顶点都处于激活态（红色标识的节点）。

第一次迭代开始：

所有顶点以EdgeDirection.Out的边方向调用sendMsg方法发送消息给目标顶点，如果 源顶点的属性+边的属性<目标顶点的属性，则发送消息。否则不发送。
发送成功的只有两条边：
5—>3(0+8<Double.Infinity , 成功),
5—>6(0+3<Double.Infinity , 成功)
3—>2(Double.Infinity+4>Double.Infinity , 失败)
3—>6(Double.Infinity+3>Double.Infinity , 失败)
2—>1(Double.Infinity+7>Double.Infinity , 失败)
2—>4(Double.Infinity+2>Double.Infinity , 失败)
2—>5(Double.Infinity+2>Double.Infinity , 失败)
4—>1(Double.Infinity+1>Double.Infinity , 失败)。

sendMsg方法执行完成之后，根据顶点处于激活态的条件，顶点5 成功地分别给顶点3 和 顶点6 发送了消息，顶点3 和 顶点6 也成功地接受到了消息。所以 此时只有5，3，6 三个顶点处于激活态，其他顶点全部钝化。然后收到消息的顶点3和顶点6都调用vprog方法，将收到的消息 与 自身的属性合并。如下图2所示。到此第一次迭代结束。

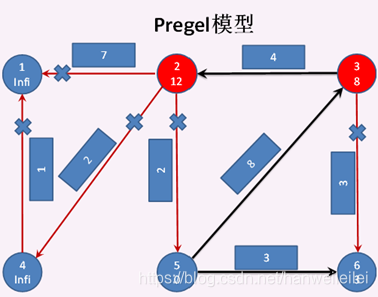
第二次迭代开始：
顶点3 给 顶点6 发送消息失败，顶点3 给 顶点2 发送消息成功，此时 顶点3 成功发送消息，顶点2 成功接收消息，所以顶点2 和 顶点3 都成为激活状态，其他顶点都成为钝化状态。然后顶点2 调用vprog方法，将收到的消息 与 自身的属性合并。 见图3. 至此第二次迭代结束。

第三次迭代开始：
顶点3分别发送消息给顶点2失败 和 顶点6失败，顶点2 分别发消息给 顶点1成功、顶点4成功、顶点5失败 ，所以 顶点2、顶点1、顶点4 成为激活状态，其他顶点为钝化状态。顶点1 和 顶点4分别调用vprog方法，将收到的消息 与 自身的属性合并。见图4。至此第三次迭代结束 

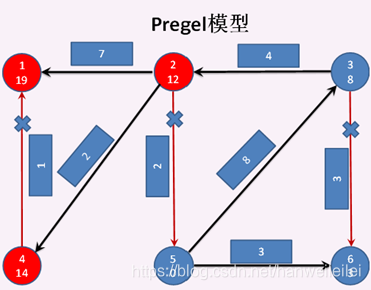
第四次迭代开始：
顶点2 分别发送消息给 顶点1失败 和 顶点4失败。顶点4 给 顶点1发送消息成功，顶点1 和 顶点4 进入激活状态，其他顶点进入钝化状态。顶点1 调用vprog方法，将收到的消息 与 自身的属性合并 。见图5

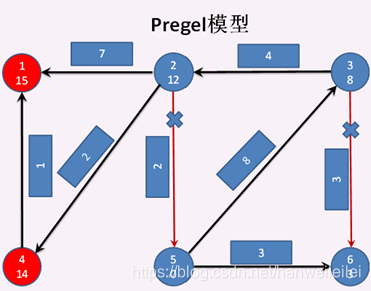
第五次迭代开始：
顶点4 再给 顶点1发送消息失败，顶点4 和 顶点1 进入钝化状态，此时全图都进入钝化状态。至此结束，见图6.