问题描述
给定一个数组, 每次操作可以选择数组中任意两个相邻的元素 x , y x, y x,y 并将其 中的一个元素替换为 gcd ( x , y ) \operatorname{gcd}(x, y) gcd(x,y), 其中 gcd ( x , y ) \operatorname{gcd}(x, y) gcd(x,y) 表示 x x x 和 y y y 的最大公约数。 请问最少需要多少次操作才能让整个数组只含 1 。
解题思路
关于 g c d gcd gcd
如果一段子数组的的 g c d gcd gcd为 1 1 1,那么原数组的 g c d gcd gcd也一定为 1 1 1。
如果存在一个子数组的 g c d gcd gcd为 1 1 1,那么这个数组无论再加上任何正整数, g c d gcd gcd也永远是 1 1 1,因为 1 1 1和任何数的 g c d gcd gcd都是 1 1 1。
1、(简单)考虑数组中是否存在 1 1 1,如果数组中存在 1 1 1,依次把全部元素变成 1 1 1,假设 1 1 1的个数为 x x x个,那么最终的答案是 n − x n-x n−x次。
(复杂——原数组中不存在 1 1 1)
2、变出一个 1 1 1,然后使用这个 1 1 1进行平推将数组全部变成 1 1 1。
3、 [ 1 , n ] [1,n] [1,n]的 g c d gcd gcd都不为 1 1 1,那么任何子数组的 g c d gcd gcd也不可能为 1 1 1,此时为无解。
问题——如何最少次数变出 1 1 1
任务转换——原数组中找到最短的子数组,使得它们的 g c d gcd gcd为1。
如果 [ l , r ] [l,r] [l,r]的 g c d gcd gcd 为 1 1 1
1、那么 [ l , r + 1 ] . . . [ l , n ] [l,r+1]...[l,n] [l,r+1]...[l,n]这些区间的 g c d gcd gcd也一定为 1 1 1,
2、而 [ l , l + 1 ] . . . [ l , r − 1 ] [l,l+1]...[l,r-1] [l,l+1]...[l,r−1]这些区间却并不一定符合条件。
二分法。对于数组中的每个数我们固定为左端点 l l l,然后去二分右端点,求出使得 区间 [ l , r ] 区间[l,r] 区间[l,r]的 g c d gcd gcd为 1 1 1的最小的右端点。这样每个数我们都定为左端点去二分它的右端点,所有答案取最小值就能找出 g c d gcd gcd位 1 1 1的最短区间。
注意:Python语言运行较慢,推荐写成st表,不推荐写线段树,线段树常数太大。
时间复杂度 O ( n l o g n ) O(nlogn) O(nlogn)。
ST算法是基于倍增思想设计的在线算法,记录从每个元素开始的连续长度为 2 k 2^k 2k的区间中元素的GCD。
预处理
类似于动态规划,规定 d p [ i ] [ j ] dp[i][j] dp[i][j]表示从第 i i i 个元素起连续 2 i 2^i 2i个数中的GCD,即记录中的最大公约数。
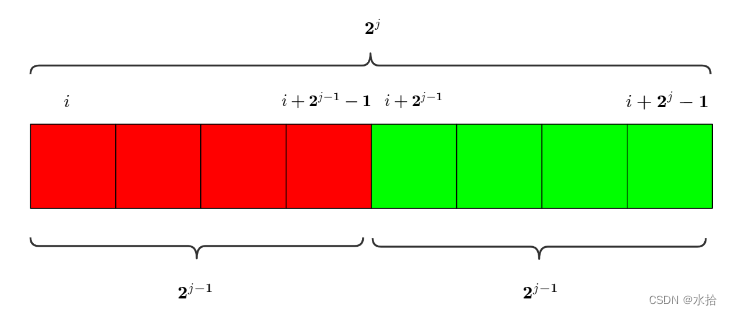
d p [ i ] [ j ] dp[i][j] dp[i][j]代表的区间 [ i , i + 2 j − 1 ] [i,i+2^j-1] [i,i+2j−1]的最大公约数,而区间 [ i , i + 2 j − 1 ] [i,i+2^j-1] [i,i+2j−1]上包含偶数个数字,故把 [ i , i + 2 j − 1 ] [i,i+2^j-1] [i,i+2j−1]平均分成两段,从 i i i 到 i + 2 j − 1 − 1 i+2^{j-1}-1 i+2j−1−1为一段, i + 2 j − 1 i+2^{j-1} i+2j−1到 i + 2 j − 1 i+2^j-1 i+2j−1为另一段,长度均为 2 j − 1 2^{j-1} 2j−1
d p [ i ] [ j ] = g c d ( d p [ i ] [ j − 1 ] , d p [ i + 2 j − 1 ] [ j − 1 ] ) dp[i][j]=gcd(dp[i][j−1],dp[i+2^{j−1}][j−1]) dp[i][j]=gcd(dp[i][j−1],dp[i+2j−1][j−1])
查询
1、不允许重叠,区间的长度按照二进制分成多个 2 2 2的整数倍区间,这些区间是求多次最大公约数能得到答案。
2、允许区间重叠,所有的情况下最多只要两个区间要求区间 , [ l , r ] [l,r] [l,r]中的最大公约数,找到一个数 k k k 使得 2 k < r − l + 1 2^k <r−l+1 2k<r−l+1,即 k = ⌊ log 2 ( r − l + 1 ) ⌋ k = \lfloor \log_2(r-l+1) \rfloor k=⌊log2(r−l+1)⌋
可以把这个区间分成两个部分: [ l , l + 2 k − 1 ] [l, l+2^k-1] [l,l+2k−1]和 [ r − 2 k + 1 , r ] [r-2^k+1, r] [r−2k+1,r]。
这两个区间恰好是刚刚已经初始化好的,前者对应的是 d p [ l ] [ k ] dp[l][k] dp[l][k],后者对应的是 d p [ r − 2 k + 1 ] [ k ] dp[r-2^k+1][k] dp[r−2k+1][k]。
Ac_code
python
# -*- coding: utf-8 -*-
# @Author : BYW-yuwei
# @Software: python3.8.6
from math import gcd
import mathdef rmq_init(arr):arr_len = len(arr)exp = int(math.log(arr_len, 2))dp = [[0] * (exp + 1) for _ in range(arr_len + 1)]for i, a in enumerate(arr):dp[i + 1][0] = afor j in range(1, exp + 1):for start in range(1, arr_len + 1):if start + (1 << j) - 1 > arr_len:breakdp[start][j] = gcd(dp[start][j - 1], dp[start + (1 << (j - 1))][j - 1])return dpdef rmq_ask(dp, left, right): k = int(math.log(right - left + 1, 2))return gcd(dp[left][k], dp[right + 1 - (1 << k)][k])n = int(input())
a = list(map(int, input().split()))cnt1 = sum(ai == 1 for ai in a)
if cnt1 > 0:print(n - cnt1)
else:dp = rmq_init(a)if rmq_ask(dp, 1, n) != 1:print(-1)else:ans = 10 ** 9for i in range(1, n):l, r = i, nwhile l < r:mid = (l + r) >> 1if rmq_ask(dp, i, mid) == 1:r = midelse:l = mid + 1if rmq_ask(dp, i, r) == 1:ans = min(ans, r-i)print(ans + n-1)