Neural network-based clustering using pairwise constraints (ICLR-workshop 2016)

源代码

摘要

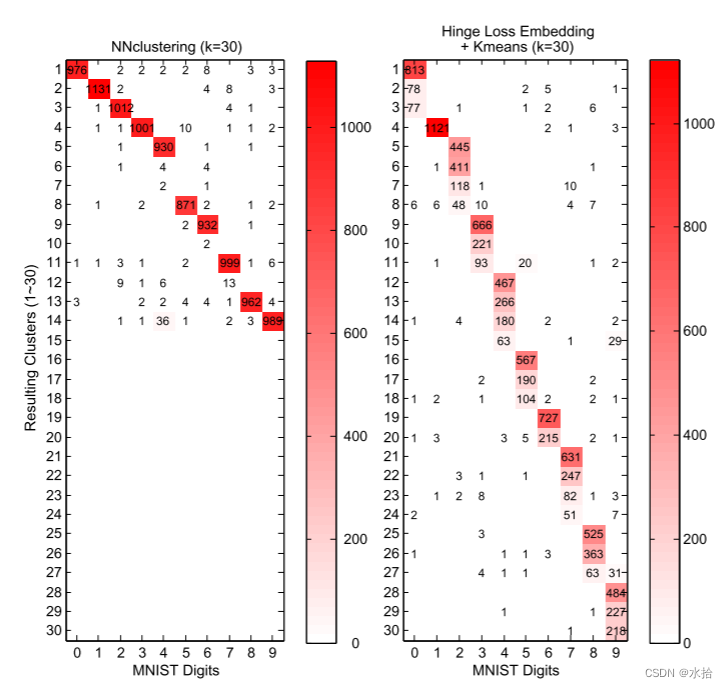
这篇论文提出了一个基于神经网络的端到端的聚类框架。我们设计了一种新策略，除了学习适用于聚类的特征嵌入，还直接在源数据利用对比方法来推动数据形成的簇。该网络通过弱标签训练——部分数据实例之间的成对关系。簇分配和分类概率是前馈网络的输出层结果。这个框架有个有趣的特征，即不需要明确指出簇中心，因此作为结果的簇分布完全是数据驱动的，没有预先定义任何距离度量。实验证明所提方法通过一个独特边缘（一个超参）击败传统两阶段方法（特征嵌入后进行k-means聚类）。和基于标准交叉熵的分类方式相比。其性能也具有相当的可比性。鲁棒性分析表明该方便对簇的数量极度不敏感，即使预定义簇数量为一个较大值，但最终占主导作用的簇的数量和真实簇的数量相近。

端到端的聚类网络

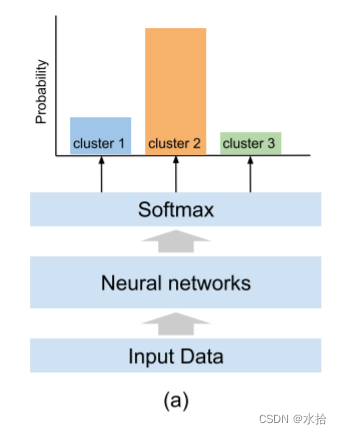
将多层感知机（vanilla multilayer preceptron）应用到分类任务：每个输出节点将预定义的标签和最小化一个损失函数的优化问题相关联，例如交叉熵，比较网络给一系列样例的输出标签（或者标签上的分布）和对应的真实标签。我们从这个模型开始，移除了标签和网络输出之间的硬关联。这个想法是只用一堆样本之间的信息，并且以一种能够表示数据集群的方式定义输出节点。换句话说，哪个节点会对应哪个簇（物体类别）是在训练过程中动态变化的。为了实现该想法。我们构思出一种只需要在为分类任务设计的神经网络的softmax层上修改代价指标的方法。因此，我们展示了一种新的逐对损失函数用于聚类，以此来取代，或者说联合传统的监督分类损失函数。这种灵活性允许网络使用这两种类型的信息，具体取决于哪一种可用。

成对的KL散度

传统softmax层的输出代表是一个样本属于不同类别的概率（也就是本文的簇），整个softmax层的输出可以看作是所给样本在可能的簇上的概率分布。
在这里插入图片描述

如果数据中仅包含一个简单的概率，如手写数字识别，那么对一个相似对而言，它们的softmax的输出分布也应该相似。相对的，如果这两个数据分属于不同的簇，那么在标签概率分布上它们也应该不一样。
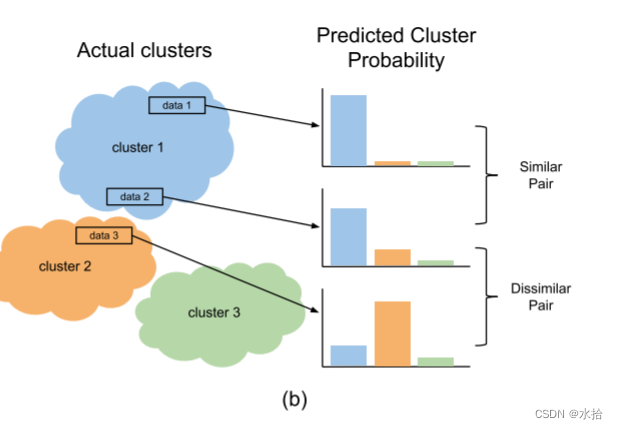
在这里插入图片描述
分布之间的距离可以通过统计距离来评估，比如KL散度。一般而言KL散度可以用来度量输出分布和真实分布之间的距离，但是，在我们的例子中，它被用来度量所给的一对实例的输出分布之间的距离。

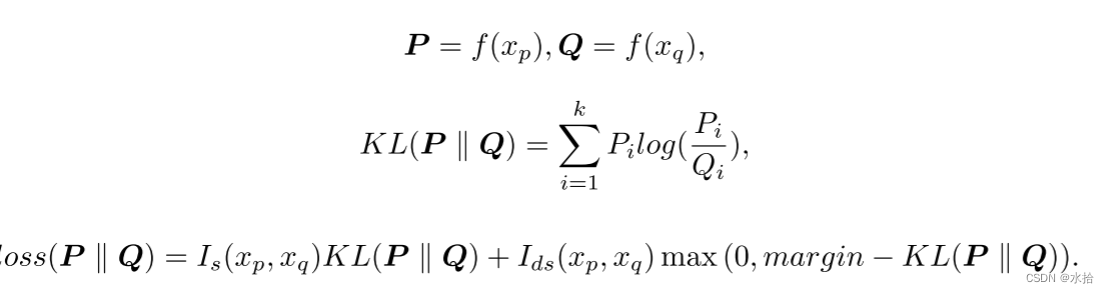
$P, Q$ 分别表示两个输入数据的输出分布（个人觉得这边的margin可能是考虑到KL散度在计算两个没有必要重叠的分布时，其结果是不具备优化意义的，所以直接截断）。因为KL散度的不对称特性，最终损失函数定义如下：
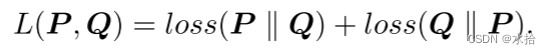
在这里插入图片描述
求导结果如下：

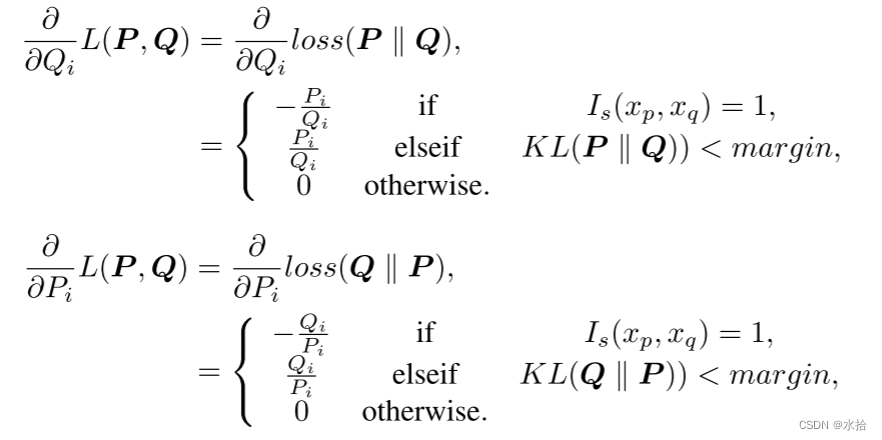
为了避免孪生网络重复喂入相同数据导致的计算冗余，该方法是将小批量数据同时喂入网络后，根据预先采样（从 $n$ 个数据，共 $n (n - 1) /2$ 种配对方式）的配对组，直接计算该批次数据总的损失，并优化网络。
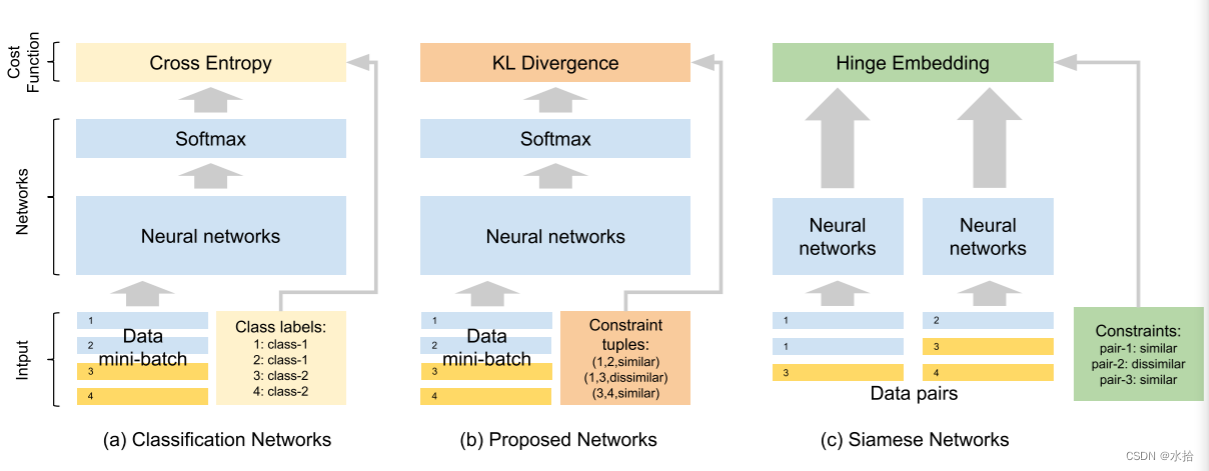
在这里插入图片描述