一、前言

众所周知，二叉树的遍历方式有三种：前序遍历、中序遍历和后序遍历。

🍌 前序遍历：首先访问根节点，然后递归遍历左子树，最后递归遍历右子树。

🍌 中序遍历：首先递归遍历左子树，然后访问根节点，最后递归遍历右子树。

🍌 后序遍历：首先递归遍历左子树，然后递归遍历右子树，最后访问根节点。

上面三种遍历方式每一种又存在两种实现形式：递归和非递归。

🍓 递归遍历二叉树：在函数内通过调用自身来完成遍历的一种方式，本质是利用函数调用栈来实现的，每次递归都要建立一个新的函数栈帧，效率较低，空间复杂度较大，更适合深度优先搜索。

🍓 非递归遍历二叉树：利用循环来遍历二叉树，用自己定义的栈来实现的，更适合广度优先搜索。

深度优先搜索（DFS）：从根节点出发，先搜索左子树，再搜索右子树的遍历方式。这种遍历方式可以使用递归来实现。

广度优先搜索（BFS）：从根节点开始，按层次遍历二叉树的方式。这种遍历方式通常不使用递归来实现，而是使用队列来实现。

二、非递归前序和中序遍历算法

下面是非递归前序和中序遍历对比（代码在下方可拷贝，代码含义详见另一篇文章戳），我们可以看出两种非递归遍历方式只是访问跟根节点的位置不同，这显然是废话！仔细看下，有没有什么新发现？如果实在是没有那就继续往下看吧。

// 先序非递归遍历
void pre_order_traverse_none(BiTree bitree)
{// 思路：先序顺序为：根节点->左子树->右子树// 当遍历完左子树之后找不到右子树// 解决方法：记住根节点stack<BiTree> stk;BiTree p = bitree;// 当前节点不为空，或者栈不为空while(p || !stk.empty()){if(p)// 根节点不为空{cout << p->data<< ",";stk.push(p);// 根指针入栈p = p->lchild;// 遍历左子树}else// 栈不为空{p = stk.top();// 获取根节点stk.pop();// 弹出根节点p = p->rchild;// 访问右子树}}}// 中序非递归遍历
void in_order_traverse_none(BiTree &bitree)
{// 思路：中序顺序为：左子树->根节点->右子树// 当遍历完左子树之后找不到根节点// 解决方法：记住根节点BiTree p = bitree;stack<BiTree> stk;while(p || !stk.empty()){if(p)// 如果根节点非空，压栈，记录根节点{stk.push(p);p = p->lchild;// 首先遍历左子树}else// 栈非空，弹出根节点{p = stk.top();cout << p->data<<" " ;stk.pop();p = p->rchild;// 访问右子树}}
}

从上面的代码对比中我们可以看出，在入栈时进行了根节点访问，访问方式即为非递归前序遍历，在弹栈时进行根节点访问，访问方式是非递归中序遍历，也就是说（敲黑板，重点来了）：

🍊 入栈时 -> 三个结点一个都未访问 -> 提供前序遍历的机会

🍊 出栈时 -> （不同根节点的）左子树遍历完成 -> 提供中序遍历的机会

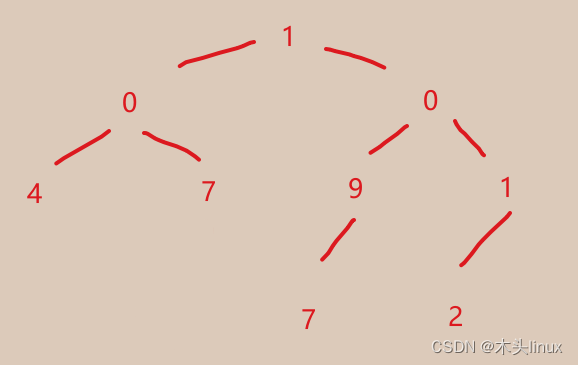
第一点大家应该都能看懂，但不出意外的话，第二点标红的地方应该出现了意外，利用下面的二叉树进行解释。

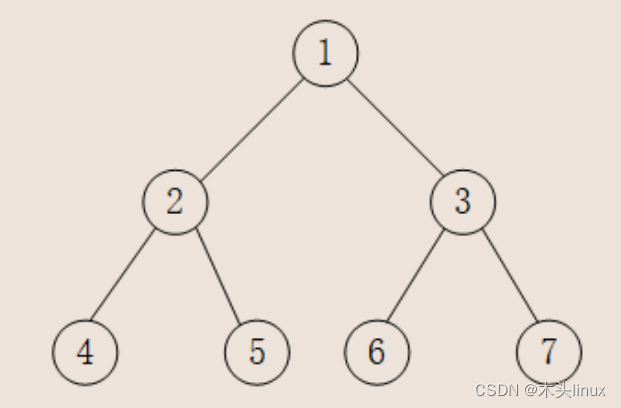
①在指向结点4的时候，首先将结点4压栈，并访问结点4的左子树，左子树为空，按照上面的代码，此时需要弹栈，栈顶为结点4，那么此时弹栈是因为结点4的左子树遍历完成。

②另一种情况，遍历到5的时候，同样先将5压栈，再访问左子树，左子树为空，同样将5弹栈，这类似于上一种情况，即5的左子树遍历完成需要弹栈。

③然后再遍历5的右子树，右子树为空，根据上方代码，同样需要弹栈，但是，注意，此时直接将1弹栈（2已经遍历过哦），仔细一看这里弹栈是因为1的左子树遍历完成了！其他情况自行尝试，现在应该明白上面的红体字了吧。

言归正传，上面的非递归前序中序遍历代码只能提供入栈和出栈时的两种遍历方式，对于非递归后序遍历无效，为什么这样说呢？又怎么修改代码呢？好的，我来解释一下：

🍐 我们可以看上面的圈3，也就是第三点，假设我们可以将上面的代码改为后序遍历的话，在遍历完5的右子树后直接访问结点1的右子树，并没有回到结点2，也就没办法进行后序遍历。

🍐 怎么修改才可以进行后序遍历呢？首先要在遍历完右子树的时候能够回到根节点，并且要区分从左子树返回和从右子树返回，因为从左子树返回需要遍历右子树，从右子树返回不需要，详见下一章。

三、非递归后序遍历算法

代码在下方，详细分析：

🍅 首先，声明了一个堆栈stk用于存储遍历过程中的节点，并声明了三个指针变量：

cur用于存储当前正在处理的节点。
last_vist用于存储上一个被访问过的节点，用于区分当前节点是从左子树返回还是从右子树返回。
top用于存储堆栈顶部的节点。

🍅 然后，定义了一个循环，每次迭代中都会执行以下操作：

如果cur 不为空，则将cur 压入堆栈中，并将cur 设置为其左子节点。
否则，取出堆栈顶部的节点，并执行以下操作：
- 如果堆栈顶部的节点有右子节点且没有被访问过，则将cur 设置为右子节点并继续遍历。
- 否则，输出堆栈顶部的节点的数据，将最后访问的节点设置为堆栈顶部的节点，并将堆栈顶部的节点弹出堆栈。

🍅 循环条件为cur 不为空或者堆栈不为空。循环结束后，后序遍历完成。

与非递归前序、中序遍历的区别：

🍉 将之前代码入栈、出栈两个操作所提供的前序、中序遍历，扩展为入栈、取栈、出栈三个操作，其中入栈代表首次遍历到根节点，取栈代表从左子树返回准备遍历右子树，出栈代表右子树为空或右子树遍历完成。（添加取栈操作，遍历完根节点右子树后会回到根结点）

🍉 使用last_visit区分左子树返回，还是右子树返回。

void post_order_traverse_none(BiTree &bitree)
{// 将每一个非#元素看作根节点遍历一遍stack<BiTree> stk;BiTree cur = bitree;BiTree last_vist = NULL;// 用来区分返回根节点时，是从左子树返回的，还是右子树返回的BiTree top = NULL;while(cur || !stk.empty()){if(cur)// 如果cur不为空，将其压入栈中，并访问左子树{stk.push(cur);cur = cur->lchild;}else// 如果当前结点cur为空，取出栈顶元素{ top = stk.top();// 取出栈顶元素if(top->rchild && last_vist != top->rchild)// 如果栈顶结点的右子节点不为空，且没有被访问过{cur = top->rchild;// 如果cur指向的左子树为空，从栈顶取出根节点，将cur指向其右子树}else// 右子节点为空，且从右子树返回（一定是右子树返回，无论右子树是否为空）{// 否则，访问栈顶元素cout<< top->data<< "输出"<<endl;// 将栈顶元素设为最后访问的元素last_vist = top;// 将栈顶元素出栈stk.pop();}}}
}