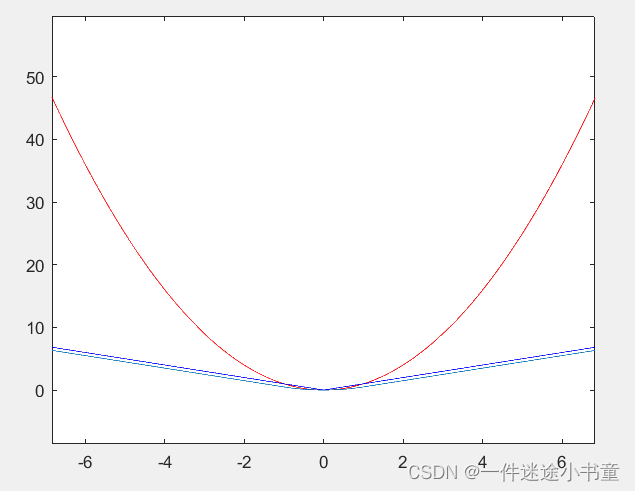
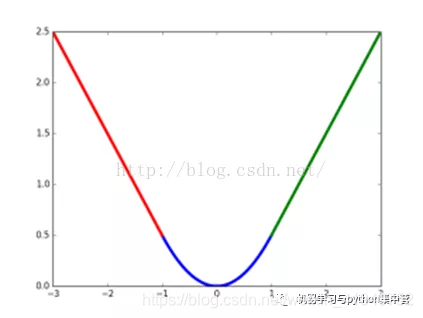
L1 loss

L1 loss的数学公式和函数图如下所示：

L1函数连续，但是在𝑦−𝑓(𝑥)=0处不可导,L1 loss大部分情况下梯度都是相等的，这意味着即使对于小的损失值，其梯度也是大的,这不利于函数的收敛和模型的学习。但是，无论对于什么样的输入值，都有着稳定的梯度，不会导致梯度爆炸问题，具有较为稳健性的解。

L2 loss(MSE loss)

MSE曲线的特点是光滑连续、可导，便于使用梯度下降算法，是比较常用的一种损失函数。而且，MSE 随着误差的减小，梯度也在减小，这有利于函数的收敛，即使固定学习因子，函数也能较快取得最小值。但是当两个值差异较大时，平方的计算方式也会容易引起梯度爆炸。下面MSE的数学公式和函数图如下所示：

在训练神经网络过程中，我们通过梯度下降算法来更新w和b，因此需要计算代价函数对w和b的导数：

然后更新w、b：

w <—— w - η* ∂C/∂w = w - η * a *σ′(z)

b <—— b - η* ∂C/∂b = b - η * a * σ′(z)

因为sigmoid函数的性质，导致σ′(z)在z取大部分值时会很小（如下图标出来的两端，几近于平坦），这样会使得w和b更新非常慢（因为η * a * σ′(z)这一项接近于0），而当两数的差异值大于1的情况下，平方的计算方式很容则到达梯度消失的区域，所以L2 loss不易与sigmod搭配使用。

L2范数将误差平方化（如果误差大于1，则误差会放大很多），模型的误差会比L1范数来得大，因此模型会对这个样本更加敏感，这就需要调整模型来最小化误差。如果这个样本是一个异常值，模型就需要调整以适应单个的异常值，这会牺牲许多其它正常的样本，因为这些正常样本的误差比这单个的异常值的误差小。

Smoth L1 loss

在Fast RCNN论文提出该方法，用于预测框和真实框之间的数值差异的损失计算，公式和对应的图如下所示：

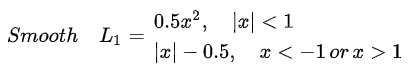
解决L1和L2的不足：

1.当预测框与 ground truth 差别过大时，梯度值不至于过大；

2.当预测框与 ground truth 差别很小时，梯度值足够小。

L1和L2的正则化

L1正则化是指权值向量w中各个元素的绝对值之和，通常表示为∣∣w∣∣1，公式如下：

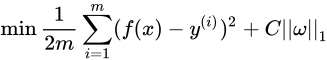
L2正则化是指权值向量w中各个元素的平方和然后再求平方根（可以看到Ridge回归的L2正则化项有平方符号），通常表示为∣∣w∣∣2，公式如下：

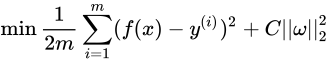
L1增加模型的稀疏性：

L1和L2正则项加入后的函数图像如下：

损失函数和正则化项图形首次相交的地方就是最优解，左图消交点(0,w)，因为正则化函数有很多突出的角（二维情况下四个，多维情况下更多），损失函数​与这些角接触的机率会远大于与其它部位接触的机率，而在这些角上会有很多权值等于0，所以L1正则化可以产生稀疏模型，进而可以用于特征选择。

L2正则化防止过拟合：

L2正则化就是在代价函数后面再加上一个正则化项。所有参数w的平方的和，除以训练集的样本大小n。λ就是正则项系数，权衡正则项与C0项的比重。另外还有一个系数1/2，1/2经常会看到，主要是为了后面求导的结果方便，后面那一项求导会产生一个2，与1/2相乘刚好凑整。公式如下：

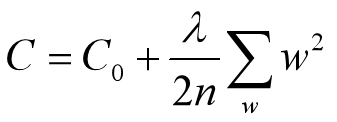
对上式进行求导并合并处理如下：

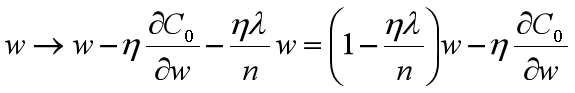
在不使用L2正则化时，求导结果中w前系数为1，现在w前面系数为 1−ηλ/n ，因为η、λ、n都是正的，所以 1−ηλ/n小于1，它的效果是减小w，这也就是权重衰减（weight decay）的由来。当然考虑到后面的导数项，w最终的值可能增大也可能减小。

拟合过程中通常都倾向于让权值尽可能小，构造一个所有参数都比较小的模型。一般认为参数值小的模型比较简单，能适应不同的数据集，也在一定程度上避免了过拟合现象。对于一个线性回归方程，若参数很大，那么只要数据偏移一点点，就会对结果造成很大的影响；但如果参数足够小，数据偏移得多一点也不会对结果造成什么影响。所以L2正则化可以防止过拟合。

Ps:当L1的正则化系数很小时，得到的最优解会很小，可以达到和L2正则化类似的效果。