一、L1、L2正则化

当样本特征很多，而样本数相对较少时，学习过程很容易陷入过拟合。为了缓解过拟合问题，可以对损失函数加入正则化项。正则化项中的Lp范数有很多，常见的有L1范数和L2范数。

    给定数据集D = {（x1，y1），（x2，y2），...，（xm，ym）}，其中x有d维特征，y∈R。我们考虑最简单的线性回归模型，以平方误差为损失函数，那么优化目标为：

     ①令p=1，即采用L1范数：

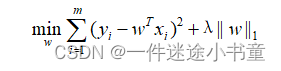
 其中正则化参数λ>0。上式被称为LASSO（Least Absolute Shrinkage and Seclction Operatro）。直译为“最小绝对收缩选择算子”，常称为LASSO。

    ②令p=2，即采用L2范数：

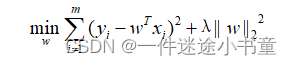
 其中正则化参数λ>0。上式被称为岭回归（ridge regression）。

    L1范数和L2范数正则化都有助于降低过拟合风险。相比之下，L1范数在x>0的时候变化率始终为1，在x<0的时候变化率始终为-1。在训练的后期，由于导数为常数1，如果学习率σ不变，损失函数会在一个稳定值附近波动，难以稳定，甚至还会出现在极值点附近“弹跳”的情况。L2范数的导数值为2x，与输入值有关。在开始阶段导数非常大，导致训练初期不稳定。

值得一提的是，L1范数还会带来一个额外的好处：它比后者更易于获得“稀疏”（sparse）解，即它求得的w会有更少的非零向量。（事实上，对w施加“稀疏约束”，也就是说希望w的非零分量尽可能少，最自然的是使用L0范数，但是L0范数不连续，难以优化求解，因此常用L1范数来近似。）

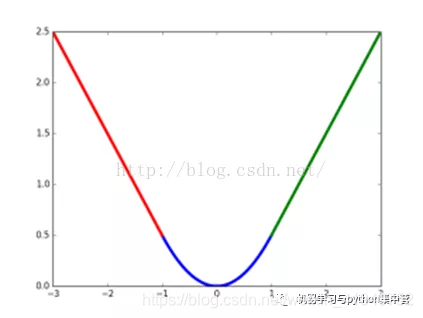
    为了理解这一点，下面给出了一个例子：假定x仅有两个属性，于是无论是L1正则还是L2正则解出的w都只有两个分量，即w1和w2，我们将其作为两个坐标轴，然后在图中绘制出L1正则和L2正则的第一项的“等值线”，即在（w1，w2）空间中平方误差项取值相同的点的连线，再分别绘制出L1范数和L2范数的等值线，即在（w1，w2）空间中L1范数取值相同的点的连线，以及L2范数取值相同的点的连线，如下图所示：

 

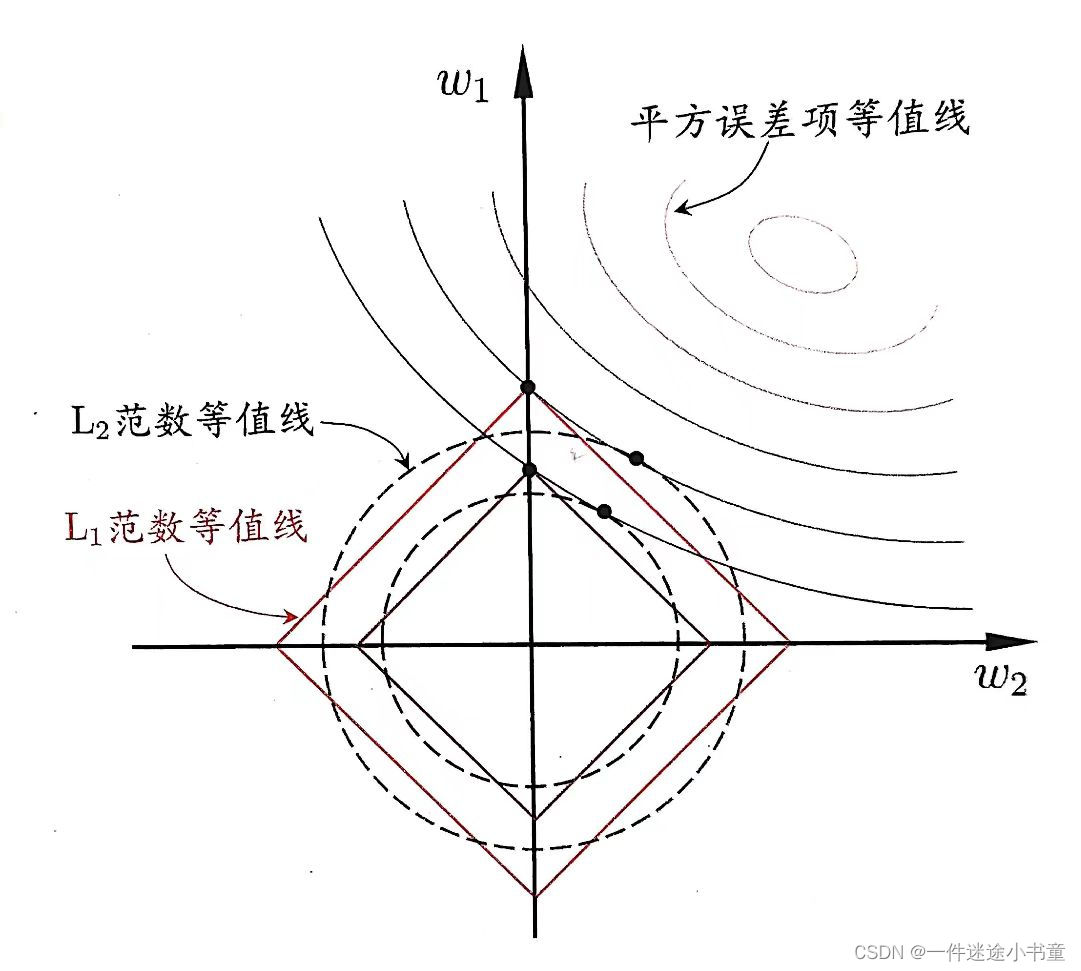
由图可以看出：采用L1范数时平方误差项等值线与正则化项等值线的交点常出现在坐标轴上，即w1或w2为0，而在采用L2范数时，两者的交点常出现在某个象限中，即w1或w2均非零。换言之，采用L1范数比L2范数更易于得到稀疏解。

 二、smooth L1 loss

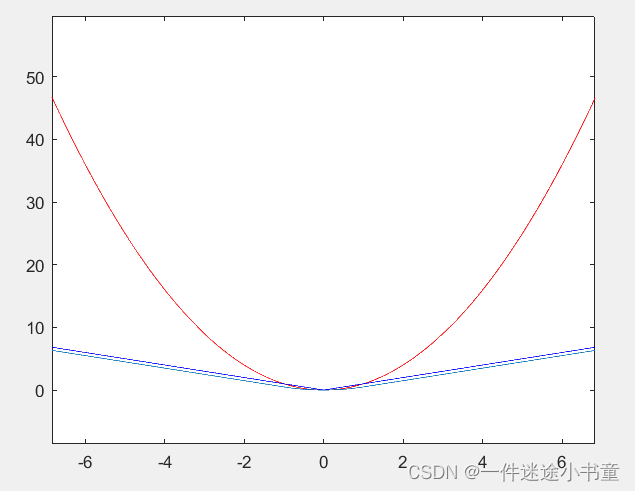
    为了克服L1和L2的不足，于是有了smooth L1 。以下是smooth L1的定义：

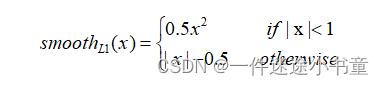
 当|x|<1的时候，x在区间[-1， 1]之间的梯度也会变得比较小，且当x=0时，函数变得可导。

 当|x|>1的时候，不再像L2一样对噪声敏感，其稳定值±1也不至于破坏网络参数。

x = -10:0.01:10;
y1 = x.*x;
y2 = abs(x);
y3 = 0.5*x.^2.*(x<1&x>-1)+(x-0.5).*(x>=1)+(-x-0.5).*(x<=-1)      ;
plot(x,y1,'r');
hold on;
plot(x,y2,'b');
hold on;
plot(x,y3)
hold on