同样存在L0、L3等,L1、L2范数应用比较多。
一个向量的 norm 就是将该向量投影到 [0, ∞) 范围内的值,其中 0 值只有零向量的 norm 取到。不难想象,将其与现实中距离进行类比,在机器学习中 norm 也就总被拿来表示距离关系:根据怎样怎样的范数,这两个向量距离多远。这里怎样怎样的范数就是范数的种类,即p-norm,严格定义为:
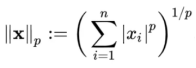
当p取1时被称为1-norm,也就是L1-norm,同理可得L2-norm。
L1和L2范数定义即为:
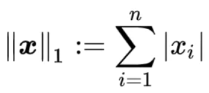
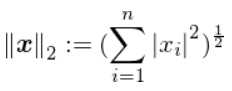
L2展开就是欧几里得范数:

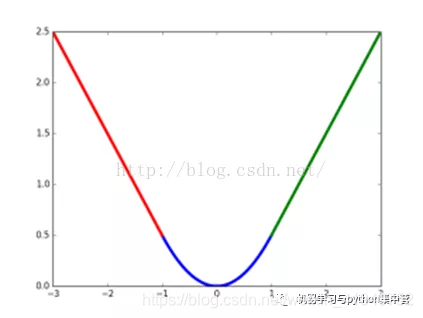
题外话,其中 L1-norm 又叫做 taxicab-norm 或者 Manhattan-norm,可能最早提出的大神直接用在曼哈顿区坐出租车来做比喻吧。下图中绿线是两个黑点的 L2 距离,而其他几根就是 taxicab 也就是 L1 距离,确实很像我们平时用地图时走的路线了。

L1 和 L2 范数在机器学习上最主要的应用大概分下面两类:
(1)作为损失函数使用
(2)作为正则项使用也即所谓 L1-regularization 和 L2-regularization
例如:(1)损失函数
在回归问题中

待解决的问题是,找出一条线,让数据点到线上的总距离(也就是error)最小。
因为范数可以表示距离,因此可以用能表示距离的L1-norm和L2-norm作为损失函数,度量预测值与实际目标之间的距离,最小化损失相当于在最小化预测值与实际值之间的距离。
- L1-norm损失函数,又称为最小绝对偏差 (least absolute deviation,LAD)。
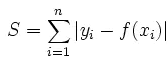
最小化损失函数,其实就是最小化预测值和目标值的绝对值。
- L2-norm损失函数,又称为最小二乘误差(least squares error, LSE)。
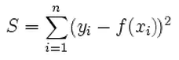
一般选择L2做损失函数,不用L1的原因:
联想一个数学问题,利用微积分求一个方程的最小值,一般步骤为:求导、置零、解方程。但如果给出一个绝对值的方程,求最小值就有点麻烦了,因为绝对值的倒数是不连续的。
在L1和L2做损失函数的选择中,也会遇到同样的问题,选择L2的原因就是:计算方便,可以直接求导获得取最小值时各个参数的取值。
此外还有一点,用L2一定只有一条最好的预测线,L1则因为其性质可能存在多个最优解。
L1也有优点,那就是鲁棒性更强,对异常值更不敏感。
(2)正则项
对于实验过程中出现的过拟合问题,正则化可以防止过拟合。从数学角度,就是在损失函数中加个正则项,防止参数过度拟合。
L1-regularization 和 L2-regularization 都是常用的正则项,公式如下:

这两个正则项主要有两点不同:
- L2可以让参数衰减,防止模型过拟合。
- L1可以产生稀疏权值矩阵,即产生一个稀疏模型,把不重要的特征直接置零,也就是特征自动选择,所以L1是一个天然的特征选择器,而L2则不会。
关于性质B,用直观的例子进行讲解。
我们常用梯度下降法优化网络,需要求导获得梯度,然后更新参数。
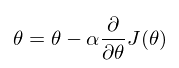
分别先对 L1 正则项和 L2 正则项来进行求导。
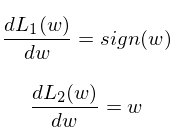
(Sign()符号函数:在数学和计算机运算中,其功能是取某个数的符号(正或负): 当x>0,sign(x)=1;当x=0,sign(x)=0; 当x<0, sign(x)=-1。)
将L1和L2和导数画在图上。

发现,在梯度更新时,不管 L1 的大小是多少(只要不是0)梯度都是1或者-1,所以每次更新时,它都是稳步向0前进。

而看 L2 的话,就会发现它的梯度会越靠近0,就变得越小。

总结:L1 防止模型过拟合的方式是产生稀疏解,实际上是减少特征数量。而 L2 是减小模型参数,尽管都能简化模型,但是一般来说 L2 模型的抗过拟合的能力更好一点。并且进一步说,L1 是假定参数符合拉普拉斯分布,L2 是假定参数符合高斯分布。
资料收集于网络资源。