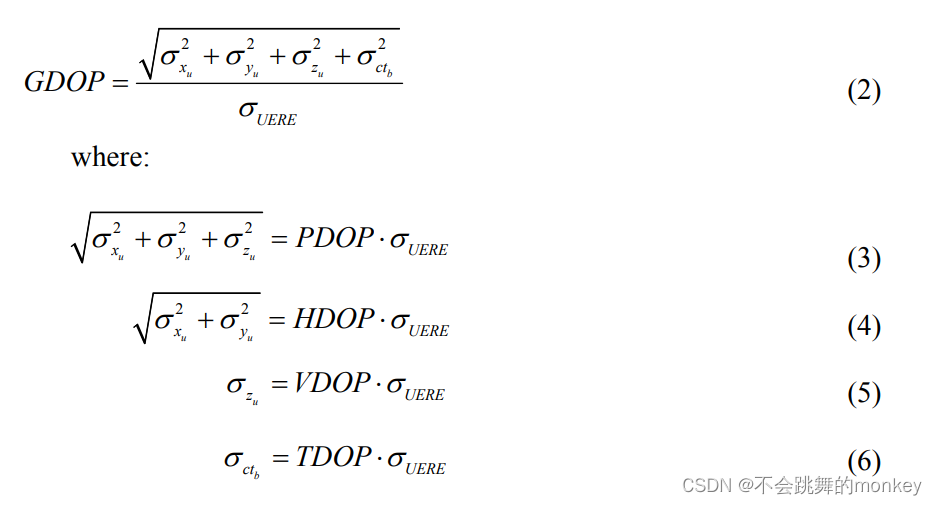上一篇伪距与载波相位中我们介绍了伪距的计算方法，也得到了包含四个未知数的GPS定位基本方程：

那么根据这个方程我们怎么来定位呢？

根据我们第一篇GPS基础原理讲过GPS的基本原理，只需已知四颗卫星的测量值，即可组成一个四元方程组，然后解出来这四个未知数。要注意的是这个方程组是一个非线性方程组，因此在实际解算过程中，常用牛顿迭代法来进行。

一、牛顿迭代法

牛顿迭代法是一个常用的解非线性方程组的方法，它将非线性方程组在一个估计解的附近进行线性化，然后求解线性化后的方程组，接着再更新解的估计值。如此反复迭代，直到解的精度满足要求为止。

相关程序思路


/*功能：基于最小二乘的单点定位参数：eAllSVPositions ((n,4) prn, sx, sy, sz, )    ：卫星编号和位置 eAllSVPositions ((n,3) PRN CNO Pseudorange)  ：卫星观测值返回：eWLSSolution 5 unknowns with two clock bias variables
*/Eigen::MatrixXd LeastSquare(Eigen::MatrixXd eAllSVPositions, Eigen::MatrixXd eAllMeasurement){Eigen::MatrixXd eWLSSolution;eWLSSolution.resize(5, 1);  // 找到有效的卫星个数（编号一样）int validNumMeasure=0;std::vector<int> validMeasure;for (int idx = 0; idx < eAllMeasurement.rows(); idx++){for (int jdx = 0; jdx < eAllSVPositions.rows(); jdx++){if (int(eAllMeasurement(idx, 0)) == int(eAllSVPositions(jdx, 0))){validNumMeasure++;  validMeasure.push_back(int(eAllMeasurement(idx, 0)));}}}// 根据上面的个数构建矩阵大小，获得有效的卫星观测值：validMeasurement，为加权最小二乘准备Eigen::MatrixXd validMeasurement;           // for WLS validMeasurement.resize(validNumMeasure,eAllMeasurement.cols());for (int idx = 0; idx < eAllMeasurement.rows(); idx++){for (int jdx = 0; jdx < eAllSVPositions.rows(); jdx++){if (int(eAllMeasurement(idx, 0)) == int(eAllSVPositions(jdx, 0))){for (int kdx = 0; kdx < eAllMeasurement.cols(); kdx++){validMeasurement(idx, kdx) = eAllMeasurement(idx, kdx);}}}}// 有效观测值的行数  int iNumSV = validMeasurement.rows();// 找到有效观测值对应的卫星数据信息（编号，位置）Eigen::MatrixXd eExistingSVPositions; // for WLSeExistingSVPositions.resize(iNumSV, eAllSVPositions.cols());for (int idx = 0; idx < validMeasurement.rows(); idx++){for (int jdx = 0; jdx < eAllSVPositions.rows(); jdx++){if (int(validMeasurement(idx, 0)) == int(eAllSVPositions(jdx, 0))){for (int kdx = 0; kdx < eAllSVPositions.cols(); kdx++){eExistingSVPositions(idx, kdx) = eAllSVPositions(jdx, kdx);}}}} // 初始化结果for (int idx = 0; idx < eWLSSolution.rows(); idx++){eWLSSolution(idx, 0) = 0; // 5*1}// 针对卫星不足的情况if (iNumSV < 5){return eWLSSolution;}bool bWLSConverge = false;int count = 0;while (!bWLSConverge){Eigen::MatrixXd eH_Matrix;eH_Matrix.resize(iNumSV, eWLSSolution.rows());Eigen::MatrixXd eDeltaPr;eDeltaPr.resize(iNumSV, 1);Eigen::MatrixXd eDeltaPos;eDeltaPos.resize(eWLSSolution.rows(), 1);for (int idx = 0; idx < iNumSV; idx++){int prn = int(validMeasurement(idx, 0));double pr = validMeasurement(idx, 2);// Calculating Geometric Distancedouble rs[3], rr[3], e[3];double dGeoDistance;rs[0] = eExistingSVPositions(idx, 1);rs[1] = eExistingSVPositions(idx, 2);rs[2] = eExistingSVPositions(idx, 3);rr[0] = eWLSSolution(0);rr[1] = eWLSSolution(1);rr[2] = eWLSSolution(2);// dGeoDistance = geodist(rs, rr, e);dGeoDistance = sqrt(pow((rs[0] - rr[0]),2) + pow((rs[1] - rr[1]),2) +pow((rs[2] - rr[2]),2));// Making H matrix      eH_Matrix(idx, 0) = -(rs[0] - rr[0]) / dGeoDistance;eH_Matrix(idx, 1) = -(rs[1] - rr[1]) / dGeoDistance;eH_Matrix(idx, 2) = -(rs[2] - rr[2]) / dGeoDistance;if (PRNisGPS(prn)){eH_Matrix(idx, 3) = 1;eH_Matrix(idx, 4) = 0;}else if (PRNisBeidou(prn)){eH_Matrix(idx, 3) = 1;eH_Matrix(idx, 4) = 1;}// Making delta pseudorangedouble rcv_clk_bias;if (PRNisGPS(prn)){rcv_clk_bias = eWLSSolution(3);       }else if (PRNisBeidou(prn)){rcv_clk_bias = eWLSSolution(4);}// double sv_clk_bias = eExistingSVPositions(idx, 4) * CLIGHT;eDeltaPr(idx, 0) = pr - dGeoDistance + rcv_clk_bias;}// Least Square Estimation eDeltaPos = (eH_Matrix.transpose() * eH_Matrix).ldlt().solve(eH_Matrix.transpose() *  eDeltaPr);//eDeltaPos = (eH_Matrix.transpose() * eH_Matrix).inverse() * eH_Matrix.transpose() *  eDeltaPr;//eDeltaPos = eH_Matrix.householderQr().solve(eDeltaPr);eWLSSolution(0) += eDeltaPos(0);eWLSSolution(1) += eDeltaPos(1);eWLSSolution(2) += eDeltaPos(2);eWLSSolution(3) += eDeltaPos(3);eWLSSolution(4) += eDeltaPos(4);for (int i = 0; i < 3; ++i){//printf("%f\n", fabs(eDeltaPos(i)));if (fabs(eDeltaPos(i)) >1e-4){bWLSConverge = false;}else { bWLSConverge = true;};}count += 1;if (count > 6)bWLSConverge = true;}std::cout << std::setprecision(12);return eWLSSolution;
}