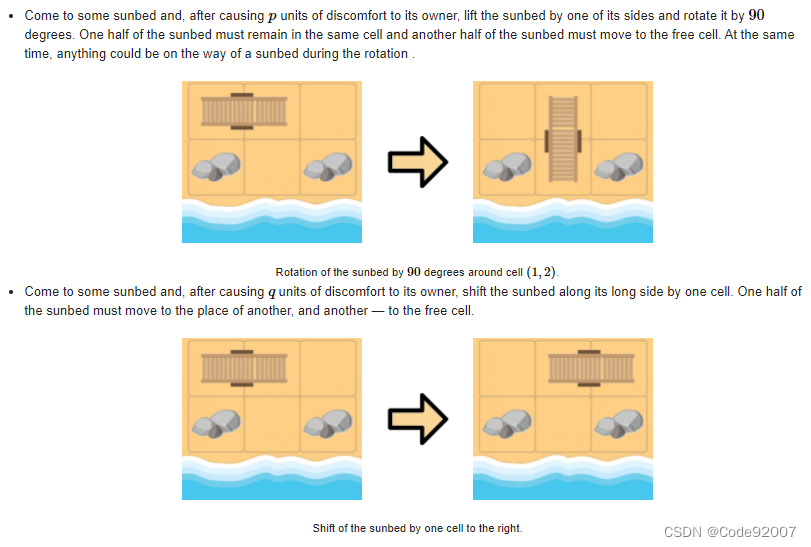
翻译：

这是这个问题的简单版本。不同之处在于，在这个版本中，数组不能包含零。只有两个版本的问题都解决了，你才能进行hack。

给定一个数组[𝑎1，𝑎2，…𝑎𝑛]，由整数−1和1组成。您必须将这个数组的一个分区构建到段集[𝑙1，𝑟1]，[𝑙2，𝑟2]，…，[𝑙𝑘，𝑟𝑘]，具有以下属性:

表示所有元素的交错和𝑖-th段的𝑠𝑖:𝑠𝑖=𝑎𝑙𝑖−𝑎𝑙𝑖+ 1 +𝑎𝑙𝑖+ 2−𝑎𝑙𝑖+ 3 +…±𝑎𝑟𝑖。例如，数组[1,0，−1,1,1]中段[2,4]的元素交替和等于0−(−1)+1=2。
𝑠𝑖对所有分区段的和应该等于零。
注意，每个𝑠𝑖不一定等于零，这个属性是𝑠𝑖在所有分区段上的和。

片段的集合(𝑙1𝑟1],[𝑙2𝑟2],…,[𝑙𝑘,𝑟𝑘)被称为分区长度的数组𝑎𝑛如果1 =𝑙1≤𝑟1,𝑙2≤𝑟2,…,𝑙𝑘≤𝑟𝑘=𝑛𝑟𝑖+ 1 =𝑙𝑖所有𝑖= 1 + 1,2,…𝑘−1。换句话说，数组的每个元素必须只属于一个段。

您必须用上面描述的属性构建给定数组的分区，或者确定这样的分区不存在。

注意，不需要最小化分区中的段数。

输入
每个测试包含多个测试用例。第一行包含测试用例的数量𝑡(1≤𝑡≤10000)。测试用例的描述如下。

每个测试用例的第一行包含一个整数𝑛(1≤𝑛≤200000)—数组𝑎的长度。

每个测试用例的第二行包含𝑛整数𝑎1，𝑎2，…，𝑎𝑛(𝑎𝑖是−1或1)-给定数组的元素。

可以保证𝑛在所有测试用例中的总和不超过200000。

输出
对于每个测试用例，如果所需的分区不存在，则打印−1。否则，打印一个整数𝑘—分区中的段数。

然后在以下𝑘行的𝑖-th中打印两个整数𝑙𝑖和𝑟𝑖—𝑖-th段的描述。应满足以下条件:

1到𝑘的每个𝑖，𝑙𝑖≤𝑟𝑖。
从1到(𝑘−1)的每个𝑖对应𝑙𝑖+1=𝑟𝑖+1。
𝑙1 = 1,𝑟𝑘=𝑛。
如果数组中有多个正确的分区，打印其中任何一个分区。

例子
inputCopy
4
4
1 1 1 1
6
-1 1 1 1 1 1
3.
1 1 1
1
1
outputCopy
1
1 - 4
2
1 3
4 - 6
－1
－1
请注意
在第一个测试用例中，我们可以构建一个长度为4的分段。这段的和等于1−1+1−1=0。

在第二个测试用例中，我们可以构建长度为3的两个段的分区。第一个段的和等于−1−1+1=−1，第二个段的和等于1−1+1=1。所以，总和等于- 1+1=0。

在第三和第四个测试用例中，可以证明没有必要的分区。

题意：将该数组分段，然后分段和按照公式来计算，所以相同的就分到一个，等于0，不相同的单个分，每次都是0，只需要判断一个n是不是奇数，奇数的话，怎么加减都不会是0。

代码实现：

#include <iostream>
#include <algorithm>
#include <string.h>
#include <string>
#include <math.h>
#include <stdio.h>
#include<vector>
#include<queue>
#include<map>
#include<set>
#include<tuple>
#include<numeric>
#include<stack>
using namespace::std;
typedef long long  ll;
int n,t;
int a[200005];
void solv(){cin>>n;for (int i =1; i<=n; i++) {cin>>a[i];}if (n%2) {printf("-1\n");return;}vector<pair<int, int>>q;for (int i =1; i<n; i+=2) {if (a[i]==a[i+1]) {q.push_back({i,i+1});}else{q.push_back({i,i});q.push_back({i+1,i+1});}}printf("%lu\n",q.size());for (int i =0; i<q.size(); i++) {printf("%d %d\n",q[i].first,q[i].second);}
}
int main(){ios::sync_with_stdio(false);cin.tie(); cout.tie();cin>>t;while (t--) {solv();}return 0;
}