题目
n*m(n*m<=3e5)的网格图,由空地、石头和1*2的床组成,
Andrew想在网格图上找一个1*2的空地用来放床,他可以把别人的床进行如下挪动:
①花费p(1<=p<=1e9)的代价,以床的一个端点为轴不动,
将另一个点顺时针或逆时针旋转90度,旋转到的点需要是空地
②花费q(1<=q<=1e9)的代价,以床的一个端点为轴不动,
将另一个点翻转180度,翻转到的点需要是空地
具体挪点方式,如下图所示:
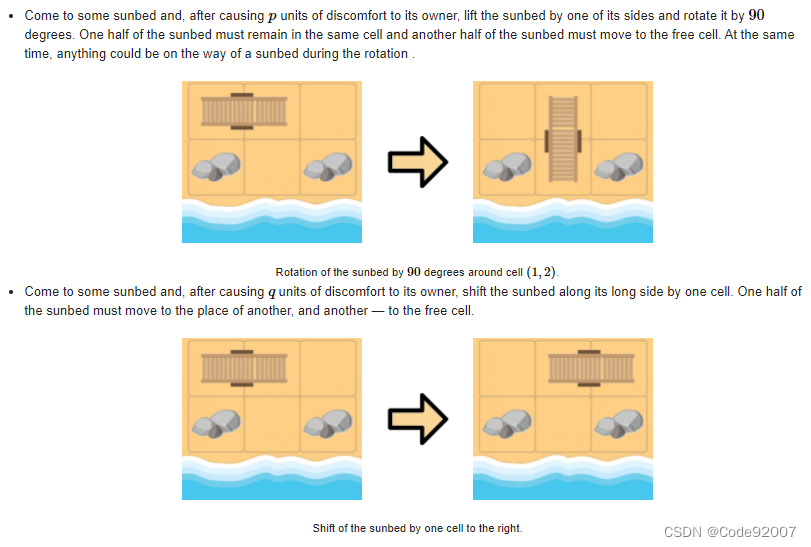
求挪动后能放下一张床的最小代价,如果无解,输出-1
实际题目的输入,是n*m的字符串,
其中,空地(.),石头(#),南北方向的床(上U下D),东西方向的床(左L右R)
思路来源
gzchenben的讲解
zhouziheng&huangxiaohua的代码
官方题解
题解
考虑如果(1,1)(1,2)的床能翻转到(1,2)(1,3),相当于空地从(1,3)挪到了(1,1),
旋转同理,我们不关注床的位置,只关注空地的位置,类似挤泡泡,将两个泡泡挤到一起,
性质一:如果将网格图黑白染色,那么旋转或翻转前后颜色不变,
因为1*2床相邻,必一黑一白,
即空地只能在同色区域内挪,
最后的答案一定是黑色区域一块空地挪若干步&白色区域一块空地挪若干步,拼接到一起,
不会出现同一块空地挪到两个位置的非法情况
性质二:每一张床只会被挪最多一次
假设一张床被挪了两次,只有三种可能,旋转2次,旋转1次翻转1次,翻转2次,
不妨翻转2次,从(1,1)(1,2)翻转到(1,3)(1,4),则说明(1,3)(1,4)本身就是空地,答案为0,
这种情况下,不如不翻,其余两种情况同理
其实注意到这些性质之后就可以做题了,
是一个多源dijkstra,黑色区域与白色区域的dij互不影响,
最后的答案是合法的位置中min(dis[i][j]+dis[i][j+1],dis[i][j]+dis[i+1][j]),
即把黑白各一块空地挪到相邻的最小代价,
心得
网格图,黑白染色后,是一个二分图,
图上已经有一些边连着(已经有一些左黑右白点之间的匹配),
现在有一些不在匹配中的边的代价是p或q,你需要花一些费用,
使得这个图的匹配数加1,求最小代价,就变成了一个标准的KM裸题,
黑点连源点s,白点连汇点t,就变成了一个标准的费用流裸题
跑流量为1的费用流即可,根据费用流的实现,
每次跑1流量的时候,实际就是跑了一个spfa,
本图无负权,所以就是dijkstra最短路
网格图的匹配转化成二分图(黑白染色)匹配,感觉是典中典啊
感觉出题人的出题来源也可能来自于此
之前还做过一道网格图匹配,黑白染色后,连左右s、t集合,转最小割的,感觉思想差不多
Caddi Programming Contest 2021(AtCoder Beginner Contest 193) F.Zebraness(最小割)_Code92007的博客-CSDN博客_atcoder 网格 网络流 最小割
代码1
代码来自zhouziheng,有个逐个读字符的小技巧,即%c前加空格
scanf(" %c",&s[ID(i,j)]);
#include<bits/stdc++.h>
using namespace std;
#define ID(i,j)(((i)-1)*m+j)
typedef long long ll;
const ll INF=1e18;
const int N=4e5+10;
char s[N];
ll p,q,dis[N];
bool vis[N];
vector<pair<int,int> >e[N];
priority_queue<pair<ll,int> > pq;
int n,m;
int main(){scanf("%d%d",&n,&m);scanf("%lld%lld",&p,&q);for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){scanf(" %c",&s[ID(i,j)]);dis[ID(i,j)]=INF;if(s[ID(i,j)]=='.'){dis[ID(i,j)]=0;pq.push(make_pair(0,ID(i,j)));}else if(s[ID(i,j)]=='R'){if(j-2>=1)e[ID(i,j-2)].push_back(make_pair(ID(i,j),q));if(i-1>=1)e[ID(i-1,j-1)].push_back(make_pair(ID(i,j),p));if(i+1<=n)e[ID(i+1,j-1)].push_back(make_pair(ID(i,j),p));}else if(s[ID(i,j)]=='L'){if(j+2<=m)e[ID(i,j+2)].push_back(make_pair(ID(i,j),q));if(i-1>=1)e[ID(i-1,j+1)].push_back(make_pair(ID(i,j),p));if(i+1<=n)e[ID(i+1,j+1)].push_back(make_pair(ID(i,j),p));}else if(s[ID(i,j)]=='U'){if(i+2<=n)e[ID(i+2,j)].push_back(make_pair(ID(i,j),q));if(j-1>=1)e[ID(i+1,j-1)].push_back(make_pair(ID(i,j),p));if(j+1<=m)e[ID(i+1,j+1)].push_back(make_pair(ID(i,j),p));}else if(s[ID(i,j)]=='D'){if(i-2>=1)e[ID(i-2,j)].push_back(make_pair(ID(i,j),q));if(j-1>=1)e[ID(i-1,j-1)].push_back(make_pair(ID(i,j),p));if(j+1<=m)e[ID(i-1,j+1)].push_back(make_pair(ID(i,j),p));}}}while(!pq.empty()){int u=pq.top().second;pq.pop();if(vis[u])continue;vis[u]=1;for(int i=0;i<e[u].size();i++){int v=e[u][i].first;if(dis[v]>dis[u]+e[u][i].second){dis[v]=dis[u]+e[u][i].second;pq.push(make_pair(-dis[v],v));}}}ll ans=INF;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(i<n)ans=min(ans,dis[ID(i,j)]+dis[ID(i+1,j)]);if(j<m)ans=min(ans,dis[ID(i,j)]+dis[ID(i,j+1)]);}}printf("%lld\n",ans==INF?-1:ans);return 0;
}代码2
代码来自huangxiaohua
建图时没有实际放入边权,巧妙地通过四个方向扩展一步后脚下踩的字母,来判断位置,
即如果是一个字母的话,就以这个字母为轴,从当前点跳到另一个字母上去,
根据(x,y)和(dx,dy)的坐标关系,决定本次+p还是+q
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;int i,j,k,n,m,t,it;
ll w1,w2,f[600500],vis[600500],res=1e18;
string s[600500];
pair<int,int> pos[600500];
vector<pair<int,int> >d={{0,1},{0,-1},{-1,0},{1,0}};int main(){ios::sync_with_stdio(0);cin>>n>>m>>w1>>w2;s[0]=s[n+1]=string(m+2,'#');for(i=1;i<=n;i++){cin>>s[i];s[i]="#"+s[i]+"#";}vector<vector<ll> >id(n+2,vector<ll>(m+2,0));for(i=1;i<=n;i++){for(j=1;j<=m;j++){id[i][j]=++it;pos[it]={i,j};f[it]=1e18;}}priority_queue<tuple<ll,int,int> >q;for(i=1;i<=n;i++)for(j=1;j<=m;j++){if(s[i][j]=='.')q.push({0,i,j});}while(!q.empty()){auto [w,x,y]=q.top();q.pop();k=id[x][y]; w=-w;if(vis[k])continue;vis[k]=1;f[k]=w;for(auto [dx,dy]:d){dx+=x;dy+=y;if(s[dx][dy]=='D'){dx--;}else if(s[dx][dy]=='U'){dx++;}else if(s[dx][dy]=='R'){dy--;}else if(s[dx][dy]=='L'){dy++;}else{continue;}if(dx<1||dx>n||dy<1||dy>m)continue;if(vis[id[dx][dy]])continue;if(dx!=x&&dy!=y){q.push({-(w+w1),dx,dy});}else{q.push({-(w+w2),dx,dy});}}}for(i=1;i<=n;i++){for(j=1;j<m;j++){res=min(res,f[id[i][j]]+f[id[i][j+1]]);}}for(i=1;i<n;i++){for(j=1;j<=m;j++){res=min(res,f[id[i][j]]+f[id[i+1][j]]);}}if(res>1e17)cout<<-1;else cout<<res;
}