【LSSVM回归预测】基于matlab灰狼算法优化最小支持向量机GWO-LSSVM数据预测【含Matlab源码 2259期】

⛄一、灰狼算法优化最小支持向量机GWO-LSSVM简介

1 算法理论
采用灰狼优化算法的最小二乘支持向量机模型预测时,为避免过拟合现象和检验该模型的有效性,将实证部分主要分为:①基于灰狼优化算法的最小二乘支持向量机预测(出现过拟合现象);②经过交叉验证的灰狼优化算法的最小二乘支持向量机预测(避免过拟合现象);③自回归积分滑动平均模型(ARIMA)预测。实证分析表明,基于灰狼优化算法的LSSVM模型预测效果优于ARIMA模型,可用于红枣产量的预测,同时也表明了灰狼优化算法对最小二乘支持向量机参数优化的合理性与有效性。

1.1 灰狼优化算法
灰狼优化(Grey Wolf Optimizer,GWO)算法是Mirjalili等在2014年提出的一种能够寻找全局最优解的新型群智能优化算法,其通过模拟灰狼群体的觅食行为实现目标优化,具有加速模型收敛速度和提高精度等特点。

该算法利用金字塔式的等级管理制度,将灰狼群体划分为4种等级:α(第1层最优灰狼)、β(第2层次优灰狼)、δ(第3层第三优灰狼)和ω(第4层剩余灰狼),并根据适应度值的大小,将狼进行排序,其中选择适应度的前3个值作为α、β和δ等级的灰狼。在狼群中,α狼做出的决策其他狼必须听从和执行,β狼协助α狼做出正确的决策,并听令于α狼,δ狼听从α和β狼,是ω狼的上级,等级最低的ω狼服从于前3等级的狼,有着平衡狼群内部关系的作用,ω狼追随前3者进行追踪和围捕,猎物的位置便是目标函数的最优解。

灰狼优化算法步骤可用数学模型表示为:
步骤1:灰狼与猎物之间的距离D

D=|GXp(t)-X(t)| (1)
式中,XP(t)表示第t代猎物的位置;X(t)为第t代灰狼的位置;G=2r1表示向量系数,r1为闭区间0到1内的随机数。

步骤2:随着灰狼向猎物的移动,利用式(2)对灰狼空间位置不断更新:
X(t+1)=Xp(t)-BD (2)
B=2ar2-a (3)

公式(2)中,X(t+1)表示第(t+1)代灰狼更新后的位置;B为收敛向量;公式(3),中r2为a的随机向量;a的分量初始值为2,其随着迭代次数的增加随之递减直至为0。

步骤3:在狼群觅食过程中,当α狼判断出猎物所处位置时,将由其带领β和δ对猎物进行追捕。因α、β和δ狼最靠近猎物,则可利用其位置判断猎物的位置。利用公式(4)和(5)求出其他灰狼与α、β和δ狼之间的距离,然后根据公式(6)判断出灰狼向猎物的移动方向即确定寻优方向。

Dk=|CiXk(t)-X(t)| (4)
Xi=Xk-μiDk (5)
Xp(t+1)=(X1+X2+X3)/3 (6)
式中,k=α,β,δ;i=1,2,3;Xp(t+1)表示第t+1代猎物的位置向量。

1.2 最小二乘支持向量机
20世纪90年代末,Suykens等提出了最小二乘支持向量机(least squares support vector machine,LSSVM),LSSVM是SVM(支持向量机)的一种改进算法,该算法在很大程度上降低了样本点在训练过程中的复杂度,有优于传统支持向量机的运算速度,是机器学习中应用较广泛的一种建模方法。

LSSVM模型常采用的核函数有高斯径向基核函数(radial basis function,RBF)、线性核函数和多项式核函数,选用RBF核函数,RBF核函数包含2个优化参数gam和sig2,其对模型的泛化能力和预测精度影响极大。

给定训练样本{xi,yi}Ni=1,则LSSVM的目标函数可表示为:
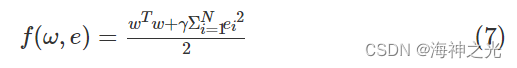
在这里插入图片描述
约束条件为:

yi=wTφ(xi)+b+ei (8)

公式(7)中w为权值;γ表示正则化参数;公式(8)中b为偏置量;ei为回归误差。

要将带有约束条件的问题转化为无约束优化问题,需要引入一个拉格朗日乘子αi,建立拉格朗日等式方程,则优化问题变为:
在这里插入图片描述
1.3 GWO-LSSVM建模
GWO-LSSVM 建模的基本思想是利用灰狼优化算法优化 LSSVM 的参数,即通过灰狼优化算法,寻找最小二乘支持向量机的2个最优参数gam和sig2,并用优化后的参数模型进行拟合与预测,其具体建模步骤如下:

第1步:输入1978—2016年全国红枣数据。
第2步:设置狼群的数量、最大迭代次数、优化参数的维数、初始化α、β和δ狼的位置以及gam、sig2的取值范围,根据狼位置所在的区间范围随时进行位置的调整。

第3步:根据gam 和 sig2的初始值以及1978—2006年数据对LSSVM模型进行训练。

第4步:计算适应度函数值。LSSVM 模型的拟合值与测量值之差的平方的均值作为适应度函数fitness。

第5步:运用灰狼优化算法在整个可行域内搜索,不断地更新α、β和δ狼以及猎物的位置,直到满足终止条件后停止迭代。适应度最小值所对应的α狼的位置为最优参数 gam和sig2。

第6步:将最优的gam和sig2作为LSSVM 模型的参数,从而对全国红枣产量进行拟合与预测。

⛄二、部分源代码

addpath(‘LSSVMlabv1_8_R2009b_R2011a’)%添加工具箱
clear
clc
tic
%% 导入训练数据
data = xlsread(‘data.xlsx’)';
[data_m,data_n] = size(data);%获取数据维度
P = 80; %百分之P的数据用于训练，其余测试
Ind = floor(P * data_m / 100);

train_data = data(1:Ind,1:end-1); %训练样本输入集
train_result = data(1:Ind,end); %训练样本输出集
test_data = data(Ind+1:end,1:end-1);% 测试样本输入集
test_result = data(Ind+1:end,end); %测试样本输出集

%% 数据归一化
[train_x,PS_i] =mapminmax(train_data’,0,1);
test_x=mapminmax(‘apply’,test_data’,PS_i);
[train_y,PS_o] = mapminmax(train_result’,0,1);
train_x=train_x’;
test_x=test_x’;
train_y=train_y’;
%% 参数初始化
type=‘f’;
kernel= ‘RBF_kernel’;
proprecess=‘proprecess’;
lb=[0.01 0.02];%参数c、g的变化的下限
ub=[1000 100];%参数c、g的变化的上限
dim=2;%此例需要优化两个参数c和g
%% 利用灰狼算法选择最佳的SVM参数c和g
SearchAgents_no=30; % 狼群数量，Number of search agents
Max_iteration=60; % 最大迭代次数，Maximum numbef of iterations

% initialize alpha, beta, and delta_pos
Alpha_pos=zeros(1,dim); % 初始化Alpha狼的位置
Alpha_score=inf; % 初始化Alpha狼的目标函数值，change this to -inf for maximization problems

Beta_pos=zeros(1,dim); % 初始化Beta狼的位置
Beta_score=inf; % 初始化Beta狼的目标函数值，change this to -inf for maximization problems

Delta_pos=zeros(1,dim); % 初始化Delta狼的位置
Delta_score=inf; % 初始化Delta狼的目标函数值，change this to -inf for maximization problems

%Initialize the positions of search agents
Positions=initialization(SearchAgents_no,dim,ub,lb);

Convergence_curve=zeros(1,Max_iteration);

l=0; % Loop counter循环计数器

% Main loop主循环
while l<Max_iteration % 对迭代次数循环
for i=1:size(Positions,1) % 遍历每个狼

   % Return back the search agents that go beyond the boundaries of the search space% 若搜索位置超过了搜索空间，需要重新回到搜索空间Flag4ub=Positions(i,:)>ub;Flag4lb=Positions(i,:)<lb;% 若狼的位置在最大值和最小值之间，则位置不需要调整，若超出最大值，最回到最大值边界；% 若超出最小值，最回答最小值边界Positions(i,:)=(Positions(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb; % ~表示取反          % 计算适应度函数值%cmd = ['gam',num2str(Positions(i,1)),'sig2 ',num2str(Positions(i,2))];%model=svmtrain(train_wine_labels,train_wine,cmd); % SVM模型训练gam=Positions(i,1);sig2=Positions(i,2);% SVM模型训练%model= trainlssvm({train_x,train_y,gam,sig2,type,kernel});%fitness=simlssvm(model,train_x);%model=trainlssvm({train_x,train_y,type,gam,sig2,kernel,proprecess});%fitness=simlssvm(model,train_x); % SVM模型预测及其精度%fitness=100-fitness(1); % 以错误率最小化为目标[alpha,b] = trainlssvm({train_x,train_y,type,gam,sig2,kernel});predict = simlssvm({train_x,train_y,type,gam,sig2,kernel},{alpha,b},train_x);fitness= sqrt(sum((predict-train_y).^2)/size(train_y,1));% Update Alpha, Beta, and Deltaif fitness<Alpha_score % 如果目标函数值小于Alpha狼的目标函数值~Alpha_score=fitness; % 则将Alpha狼的目标函数值更新为最优目标函数值，Update alphaAlpha_pos=Positions(i,:); % 同时将Alpha狼的位置更新为最优位置end