写在前面： 可惜了，如果做出第四道，应该可以直接回青名的，这次前三道的手感都不错，可惜第四道没做出，思路都想对了，但是没写出来。
祝大家新年快乐！！！

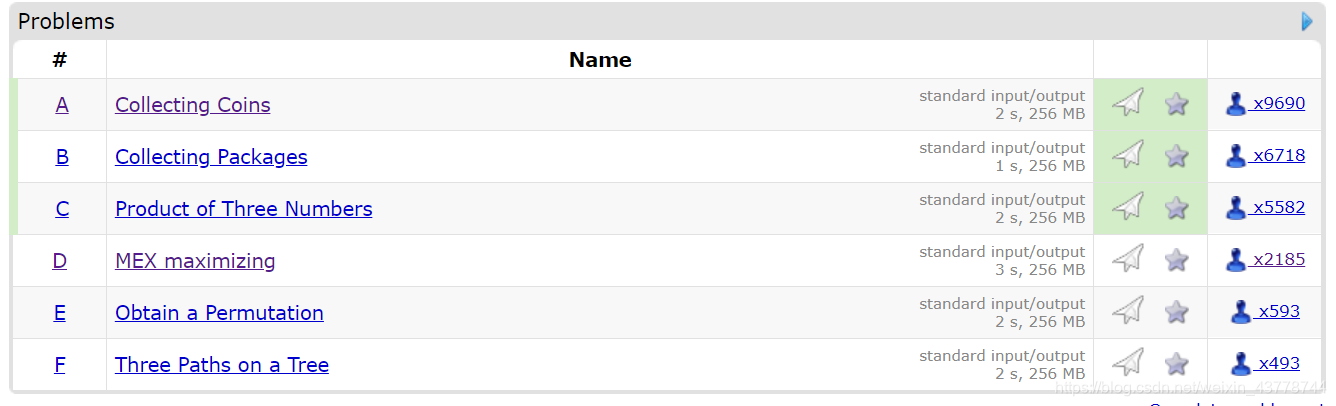
A. Collecting Coins

time limit per test2 seconds
memory limit per test256 megabytes
inputstandard input
outputstandard output
Polycarp has three sisters: Alice, Barbara, and Cerene. They’re collecting coins. Currently, Alice has a coins, Barbara has b coins and Cerene has c coins. Recently Polycarp has returned from the trip around the world and brought n coins.

He wants to distribute all these n coins between his sisters in such a way that the number of coins Alice has is equal to the number of coins Barbara has and is equal to the number of coins Cerene has. In other words, if Polycarp gives A coins to Alice, B coins to Barbara and C coins to Cerene (A+B+C=n), then a+A=b+B=c+C.

Note that A, B or C (the number of coins Polycarp gives to Alice, Barbara and Cerene correspondingly) can be 0.

Your task is to find out if it is possible to distribute all n coins between sisters in a way described above.

You have to answer t independent test cases.

Input
The first line of the input contains one integer t (1≤t≤104) — the number of test cases.

The next t lines describe test cases. Each test case is given on a new line and consists of four space-separated integers a,b,c and n (1≤a,b,c,n≤108) — the number of coins Alice has, the number of coins Barbara has, the number of coins Cerene has and the number of coins Polycarp has.

Output
For each test case, print “YES” if Polycarp can distribute all n coins between his sisters and “NO” otherwise.

Example
inputCopy
5
5 3 2 8
100 101 102 105
3 2 1 100000000
10 20 15 14
101 101 101 3
outputCopy
YES
YES
NO
NO
YES
思路： 看他们加起来是不是3的倍数，并且三分以后是不是都大于原来的abc。

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <string>
#include <cstring>
#include <cmath>using namespace std;#define endl '\n'typedef long long ll;int a[10004];int main()
{ll a, b, c, n, t;cin >> t;while (t--){cin >> a >> b >> c >> n;ll x = (a + b + c + n) % 3;ll k = (a + b + c + n) / 3;ll f = 0;if (k - a >= 0 && k - b >= 0 && k - c >= 0)f = 1;if (f == 1 && x == 0)cout << "YES" << endl;elsecout << "NO" << endl;}return 0;
}

B. Collecting Packages

time limit per test1 second
memory limit per test256 megabytes
inputstandard input
outputstandard output
There is a robot in a warehouse and n packages he wants to collect. The warehouse can be represented as a coordinate grid. Initially, the robot stays at the point (0,0). The i-th package is at the point (xi,yi). It is guaranteed that there are no two packages at the same point. It is also guaranteed that the point (0,0) doesn’t contain a package.

The robot is semi-broken and only can move up (‘U’) and right (‘R’). In other words, in one move the robot can go from the point (x,y) to the point (x+1,y) or to the point (x,y+1).

As we say above, the robot wants to collect all n packages (in arbitrary order). He wants to do it with the minimum possible number of moves. If there are several possible traversals, the robot wants to choose the lexicographically smallest path.

The string s of length n is lexicographically less than the string t of length n if there is some index 1≤j≤n that for all i from 1 to j−1 si=ti and sj<tj. It is the standard comparison of string, like in a dictionary. Most programming languages compare strings in this way.

Input
The first line of the input contains an integer t (1≤t≤100) — the number of test cases. Then test cases follow.

The first line of a test case contains one integer n (1≤n≤1000) — the number of packages.

The next n lines contain descriptions of packages. The i-th package is given as two integers xi and yi (0≤xi,yi≤1000) — the x-coordinate of the package and the y-coordinate of the package.

It is guaranteed that there are no two packages at the same point. It is also guaranteed that the point (0,0) doesn’t contain a package.

The sum of all values n over test cases in the test doesn’t exceed 1000.

Output
Print the answer for each test case.

If it is impossible to collect all n packages in some order starting from (0,0), print “NO” on the first line.

Otherwise, print “YES” in the first line. Then print the shortest path — a string consisting of characters ‘R’ and ‘U’. Among all such paths choose the lexicographically smallest path.

Note that in this problem “YES” and “NO” can be only uppercase words, i.e. “Yes”, “no” and “YeS” are not acceptable.

Example
inputCopy
3
5
1 3
1 2
3 3
5 5
4 3
2
1 0
0 1
1
4 3
outputCopy
YES
RUUURRRRUU
NO
YES
RRRRUUU
Note
For the first test case in the example the optimal path RUUURRRRUU is shown below:

B. Collecting Packages
time limit per test1 second
memory limit per test256 megabytes
inputstandard input
outputstandard output
There is a robot in a warehouse and n packages he wants to collect. The warehouse can be represented as a coordinate grid. Initially, the robot stays at the point (0,0). The i-th package is at the point (xi,yi). It is guaranteed that there are no two packages at the same point. It is also guaranteed that the point (0,0) doesn’t contain a package.

The robot is semi-broken and only can move up (‘U’) and right (‘R’). In other words, in one move the robot can go from the point (x,y) to the point (x+1,y) or to the point (x,y+1).

As we say above, the robot wants to collect all n packages (in arbitrary order). He wants to do it with the minimum possible number of moves. If there are several possible traversals, the robot wants to choose the lexicographically smallest path.

The string s of length n is lexicographically less than the string t of length n if there is some index 1≤j≤n that for all i from 1 to j−1 si=ti and sj<tj. It is the standard comparison of string, like in a dictionary. Most programming languages compare strings in this way.

Input
The first line of the input contains an integer t (1≤t≤100) — the number of test cases. Then test cases follow.

The first line of a test case contains one integer n (1≤n≤1000) — the number of packages.

The next n lines contain descriptions of packages. The i-th package is given as two integers xi and yi (0≤xi,yi≤1000) — the x-coordinate of the package and the y-coordinate of the package.

It is guaranteed that there are no two packages at the same point. It is also guaranteed that the point (0,0) doesn’t contain a package.

The sum of all values n over test cases in the test doesn’t exceed 1000.

Output
Print the answer for each test case.

If it is impossible to collect all n packages in some order starting from (0,0), print “NO” on the first line.

Otherwise, print “YES” in the first line. Then print the shortest path — a string consisting of characters ‘R’ and ‘U’. Among all such paths choose the lexicographically smallest path.

Note that in this problem “YES” and “NO” can be only uppercase words, i.e. “Yes”, “no” and “YeS” are not acceptable.

Example
inputCopy
3
5
1 3
1 2
3 3
5 5
4 3
2
1 0
0 1
1
4 3
outputCopy
YES
RUUURRRRUU
NO
YES
RRRRUUU
Note
For the first test case in the example the optimal path RUUURRRRUU is shown below:

思路： 开始以为要搜索，后来发现只要排序后判断就行。

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <string>
#include <cstring>
#include <cmath>using namespace std;#define endl '\n'typedef long long ll;struct node {ll x;ll y;
};bool cmp(node a, node b)
{if (a.x != b.x)return a.x < b.x;return a.y < b.y;
}int main()
{ll a, b, c, n, t;cin >> t;while (t--){node p[1001];cin >> n;for (int i = 0; i < n; ++i){cin >> p[i].x >> p[i].y;}sort(p, p + n, cmp);int f = 0;for (int i = 1; i < n; ++i){if (p[i - 1].y > p[i].y){f = 1;break;}}if (f){cout << "NO" << endl;continue;}cout << "YES" << endl;int x = 0;int y = 0;for (int i = 0; i < n; ++i){while (x < p[i].x){cout << "R";x++;}while (y < p[i].y){cout << "U";y++;}}cout << endl;}return 0;
}

C. Product of Three Numbers

time limit per test2 seconds
memory limit per test256 megabytes
inputstandard input
outputstandard output
You are given one integer number n. Find three distinct integers a,b,c such that 2≤a,b,c and a⋅b⋅c=n or say that it is impossible to do it.

If there are several answers, you can print any.

You have to answer t independent test cases.

Input
The first line of the input contains one integer t (1≤t≤100) — the number of test cases.

The next n lines describe test cases. The i-th test case is given on a new line as one integer n (2≤n≤109).

Output
For each test case, print the answer on it. Print “NO” if it is impossible to represent n as a⋅b⋅c for some distinct integers a,b,c such that 2≤a,b,c.

Otherwise, print “YES” and any possible such representation.

Example
inputCopy
5
64
32
97
2
12345
outputCopy
YES
2 4 8
NO
NO
NO
YES
3 5 823
思路： 素数判断的一种变体，基本还是素数判断那一套，找两个因数，除出来最后一个也是。

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <string>
#include <cstring>
#include <cmath>using namespace std;#define endl '\n'typedef long long ll;int main()
{ll a, b, c, n, t;cin >> t;while (t--){cin >> n;int f = 0;ll m = n;ll i = 2;for (i = 2; i <= sqrt(n); ++i){if (n % i == 0){f++;n /= i;if (f == 2)break;}}if (f == 2 && i != n){cout << "YES" <<endl;}else{cout << "NO" << endl;continue;}f = 0;for (i = 2; i <= sqrt(m); ++i){if (m % i == 0){cout << i << " ";f++;m /= i;if (f == 2)break;}}cout << n << endl;}return 0;
}

D. MEX maximizing

time limit per test3 seconds
memory limit per test256 megabytes
inputstandard input
outputstandard output
Recall that MEX of an array is a minimum non-negative integer that does not belong to the array. Examples:

for the array [0,0,1,0,2] MEX equals to 3 because numbers 0,1 and 2 are presented in the array and 3 is the minimum non-negative integer not presented in the array;
for the array [1,2,3,4] MEX equals to 0 because 0 is the minimum non-negative integer not presented in the array;
for the array [0,1,4,3] MEX equals to 2 because 2 is the minimum non-negative integer not presented in the array.
You are given an empty array a=[] (in other words, a zero-length array). You are also given a positive integer x.

You are also given q queries. The j-th query consists of one integer yj and means that you have to append one element yj to the array. The array length increases by 1 after a query.

In one move, you can choose any index i and set ai:=ai+x or ai:=ai−x (i.e. increase or decrease any element of the array by x). The only restriction is that ai cannot become negative. Since initially the array is empty, you can perform moves only after the first query.

You have to maximize the MEX (minimum excluded) of the array if you can perform any number of such operations (you can even perform the operation multiple times with one element).

You have to find the answer after each of q queries (i.e. the j-th answer corresponds to the array of length j).

Operations are discarded before each query. I.e. the array a after the j-th query equals to [y1,y2,…,yj].

Input
The first line of the input contains two integers q,x (1≤q,x≤4⋅105) — the number of queries and the value of x.

The next q lines describe queries. The j-th query consists of one integer yj (0≤yj≤109) and means that you have to append one element yj to the array.

Output
Print the answer to the initial problem after each query — for the query j print the maximum value of MEX after first j queries. Note that queries are dependent (the array changes after each query) but operations are independent between queries.

Examples
inputCopy
7 3
0
1
2
2
0
0
10
outputCopy
1
2
3
3
4
4
7
inputCopy
4 3
1
2
1
2
outputCopy
0
0
0
0
Note
In the first example:

After the first query, the array is a=[0]: you don’t need to perform any operations, maximum possible MEX is 1.
After the second query, the array is a=[0,1]: you don’t need to perform any operations, maximum possible MEX is 2.
After the third query, the array is a=[0,1,2]: you don’t need to perform any operations, maximum possible MEX is 3.
After the fourth query, the array is a=[0,1,2,2]: you don’t need to perform any operations, maximum possible MEX is 3 (you can’t make it greater with operations).
After the fifth query, the array is a=[0,1,2,2,0]: you can perform a[4]:=a[4]+3=3. The array changes to be a=[0,1,2,2,3]. Now MEX is maximum possible and equals to 4.
After the sixth query, the array is a=[0,1,2,2,0,0]: you can perform a[4]:=a[4]+3=0+3=3. The array changes to be a=[0,1,2,2,3,0]. Now MEX is maximum possible and equals to 4.
After the seventh query, the array is a=[0,1,2,2,0,0,10]. You can perform the following operations:
a[3]:=a[3]+3=2+3=5,
a[4]:=a[4]+3=0+3=3,
a[5]:=a[5]+3=0+3=3,
a[5]:=a[5]+3=3+3=6,
a[6]:=a[6]−3=10−3=7,
a[6]:=a[6]−3=7−3=4.
The resulting array will be a=[0,1,2,5,3,6,4]. Now MEX is maximum possible and equals to 7.
思路： 这题当时没打出来。。。但我思路已经想到了，就差了最后一个循环55555.
以后还要更认真的训练！！！
其实是模数递增，然后找空位。

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <string>
#include <cstring>
#include <cmath>using namespace std;#define endl '\n'typedef long long ll;ll a[400005];int main()
{ ll m = 0, n, x, k;cin >> n >> x;for (int i = 0; i < n; ++i){cin >> k;a[k % x]++;while (a[m % x] > m / x)m++;cout << m << endl;}return 0;
}