数字图像处理课程设计

一、前言

《数字图像处理》是一门应用型课程，为了更巩固和掌握图像处理技术的基本技能，提高实际动手能力，并通过实际编程了解图像处理算法实现的基本原理，为今后应用图像处理技术和编程技术解决实际问题奠定基础，设计一个GUI界面实现图像处理的交互界面。

二、设计目标

1、该程序用python tkinter库设计GUI界面，实现图像处理交互式操作
2、可实现绘制灰度直方图及直方图均衡化
3、灰度变换，如：灰度反转、对数变换、线性变换
4、几何变换，如：图像放大、缩小、旋转、位移
5、图像加噪声（椒盐噪声与高斯噪声）、空域和频域去噪
6、边缘提取，采用robert，sobel，拉普拉斯算子对图像进行边缘提取

三、程序设计

1、GUI界面设计

GUI界面采用的是python的第三方库tkinter来搭建的。整体GUI界面分为信息框、原图预览框、参数框、结果显示框四个区域。信息框用来显示个人基本信息；原图预览框用来导入预处理的图片并显示，以及图像处理方式的选择；参数框用来输入参数；结果显示框用来显示图像处理后的结果。GUI界面如图：
Alt
Alt

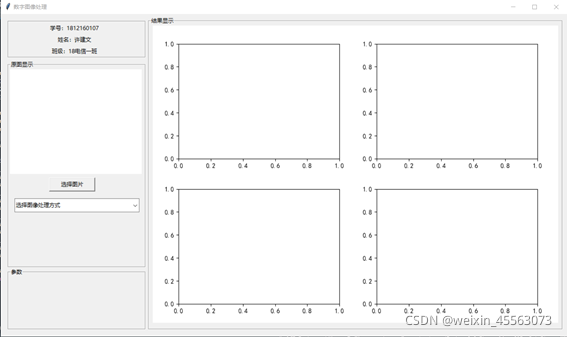
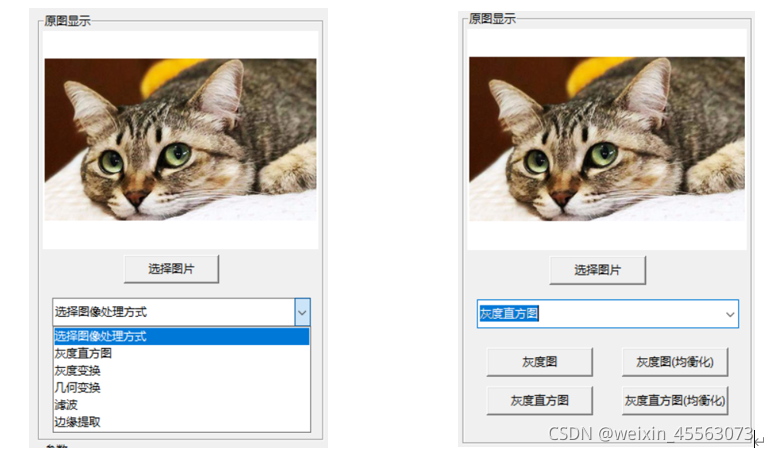
其中，用LabelFrame划分各个区域，在原图显示区域中，点击选择图片按钮选择图片，选择的图片会在Label2上显示出来，下方的下拉框是用来选择图像处理方式，最后处理结果会在右侧显示区域画布控件canvas_spice上绘制出来。

2、灰度直方图均衡化

直方图均衡化是通过拉伸像素强度分布范围来增强图像对比度的一种方法。直方图均衡化是通过调整图像的灰阶分布，使得在0~255灰阶上的分布更加均衡，提高了图像的对比度，达到改善图像主观视觉效果的目的。
均衡化过程：
1.将彩色图片转换为灰度图片，统计各灰度级的像素数目；
2.将每一个灰度级的像素的个数/图像的像素总数得到每一灰度的出现概率；
3.最后用每一级灰度值×该灰度出现概率得到灰度分布情况，实现灰度均衡。
下图是图像原灰度图与灰度均衡化后的图像对比与直方图对比：
Alt

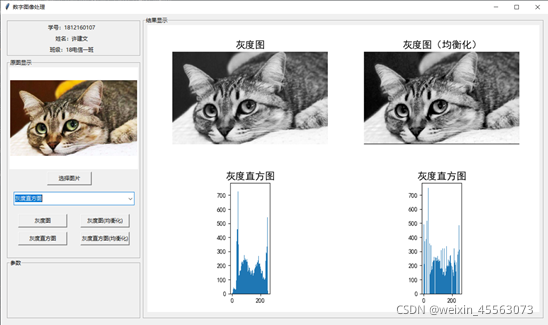
从结果图中可以看到，均衡化后的图比原灰度图相比，对比度明显提高了，也更加清晰了，而均衡化后的直方图在坐标轴上的分布也更为平均。

3、灰度变换

（1）灰度反转
黑白图像的反转其实就是将灰度值为1的像素变为0，灰度值为0的像素变为1。而对有256灰度级的图像来说，就是用255减去原图像各个像素的灰度值。
（2）对数变换
对数变换是对原图像灰度值动态范围进行压缩，对数变换的公式可表示为： g(x,y)=c*log⁡(1+f(x,y))，主要用于调高输入图像的低灰度值。
（3）线性变换
线性变换是通过建立灰度映射来调整原始图像的灰度，从而改善图像的质量，凸显图像的细节，提高图像的对比度。线性变换的计算公式:g(x)=αf(x)+β。
下图是各灰度变换后的结果：
Alt
Alt

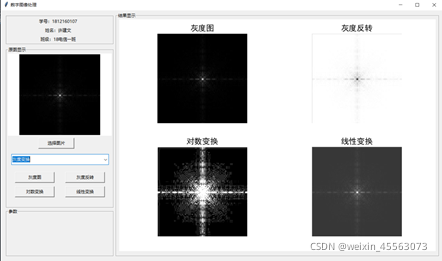
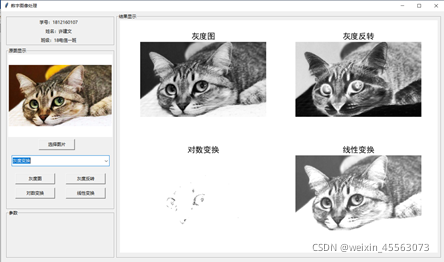
4、几何变换

（1）缩放
缩放是对图像进行放大或缩小。图像放大就是将原图像中的每一个像素复制到放大新图像对应的像素乘上倍数，这种方法叫最近领域插值法，本设计的放大倍数为2，也就是将原图像的像素复制到新图像对应的2各像素上；本设计使用的缩小方法是将图像的行和列缩小一半，从整体上就是将原图像缩小为原来的四分之一。
（2）旋转
图像旋转是以图像的中心为原点，将图像中的像素旋转同一个角度达到整体图像的旋转。本程序中使用cv2.getRotationMatrix2D()函数取图像中点逆时针旋转90°。
（3）位移
图像位移是指将一幅图像或一幅图像中的子图像块按指定的x方向和y方向的偏移量△x和△y进行位移。程序中使用cv2.warpAffine()以H为变换矩阵进行图像平移，其中变换矩阵H为[1,0,50],[0,1,25] 。
下图为图像几何变换后的结果图：
Alt
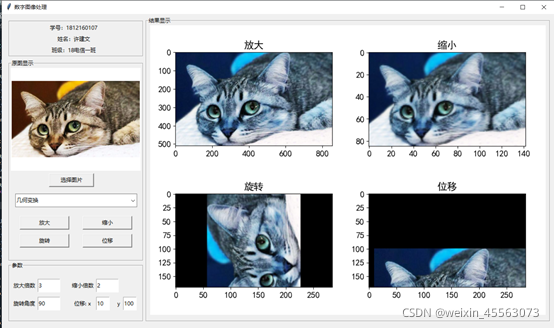
通过给设定相关参数执行对于程序，实现图片的放大、缩小、旋转以及位移。上图是放大3倍、缩小2倍、顺时针旋转90度和向下平移100像素，向右平移10像素，这里的放大与缩小后的图像是设置与画布大小一致的，可以通过图片的坐标轴查看具体像素。

5、图像加噪及滤波

（1）椒盐噪声
椒盐噪声是指两种噪声，一种是盐噪声，另一种是胡椒噪声。盐=白色(0)，椒=黑色(255)。前者是高灰度噪声，后者属于低灰度噪声。一般两种噪声同时出现，呈现在图像上就是黑白杂点，类似椒盐，故称为椒盐噪声。
添加椒盐噪声的原理是：首先设置一个阈值即噪声比例，然后随机生成0-1之间的数字，如果生成的随机数小于噪声比例则将该像素点添加黑点，即椒噪声，如果生成的随机数大于（1-噪声比例）则将该像素点添加白点，即盐噪声，这样就能够得到要添加的椒盐噪点，最后将这些噪点与原图像相加，得到噪声污染后的图像。
下图为添加噪声后的图与所添加的噪点图：
Alt
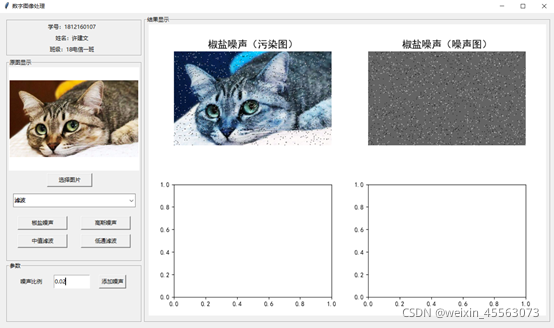
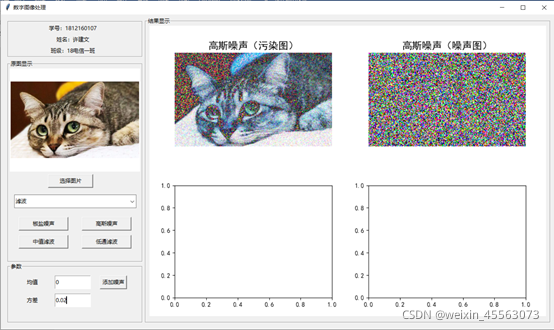
（2）高斯噪声
高斯噪声是指它的概率密度函数服从高斯分布的一类噪声。如果一个噪声，它的幅度分布服从高斯分布，而它的功率谱密度又是均匀分布的，则称它为高斯白噪声。
添加高斯噪声的原理是：首先将原始图像的像素值进行归一化，然后设置一个均值与方差呈高斯分布的图像矩阵，将噪声和原始图像进行相加得到加噪后的图像，clip函数将元素的大小限制在了low_clip和1之间了，小于的用low_clip代替，大于1的用1代替，解除归一化，乘以255将加噪后的图像的像素值恢，这样就得到添加噪声后的图像了。
下图为添加噪声后的图与所添加的噪声图：
Alt

（3）空域滤波（中值滤波）
中值滤波是一种非线性滤波器，在一定程度上可以克服线性平滑滤波器所引起的图像模糊问题。其基本原理是基于某种中值滤波窗口，对该窗口覆盖的所有像素的灰度进行排序，用其中间值代替图像中被该窗口覆盖的所有像素的中点像素的灰度值，从而弥补了领域平均噪声消除方法的不足。
本次使用的是cv2中的medianBlur（img,k）函数进行滤波，其中img参数是要处理的图像，k代表窗口的尺寸，下图分别为使用中值滤波处理椒盐噪声和处理高斯噪声的结果：
Alt
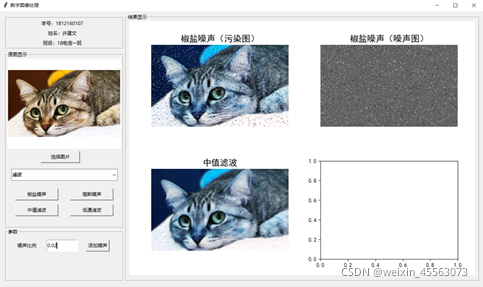
通过上面结果我们可以看到，中值滤波对于消除图像中的椒盐噪声非常有效，效果很好，在滤除噪声的同时能很好的保护信号的细节信息，但是对高斯噪声的处理结果却非常差，所以不建议使用中值滤波处理高斯噪声。
（4）频域滤波（低通滤波）
理想低通滤波器的含义是在半径为D0的圆内的所有频率没有衰减地通过该滤波器；而在此半径的圆之外的所有频率完全被衰减掉。D0称为截止频率。一个理想的低通滤波器的转移函数定义为：
Alt
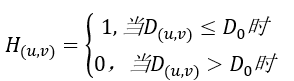
实现过程：①将图片转换为数组并将其进行傅里叶变换；②将低频移动到中间；③使用一个矩形窗口对图像进行掩模操作去除高频分量；④再将得到的结果进行傅里叶逆变换；⑤最后进行归一化。
在编写程序过程中，在这一步遇到了问题，当执行低通滤波时，会出现结果是一张黑图，原因可能是图片格式不符，而且执行完低通滤波后就不能执行其他程序了，没有找到解决的方法。下图为单独使用低通滤波函数对高斯噪声和对椒盐噪声处理的结果：
Alt

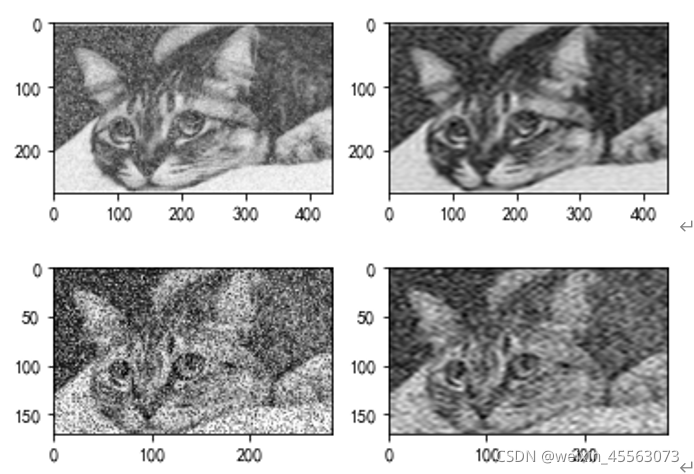
通过上面结果我们可以看到，中值滤波对于消除图像中的高斯噪声效果好一些，但是对椒盐噪声的处理结果却非常差。

6、边缘提取

（1）Robert算子
任意一堆互相垂直方向上的差分可以看成是梯度的近似求解，Robert边缘检测算子就是基于该原理，用对角线上相邻像素之差来代替梯度寻找边缘。Robert算子模板可以表示为
Alt
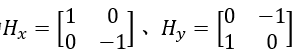
检测步骤：利用算子模板对图像进行像素卷积，将两个结果相加，判断结果是否大于阈值，若满足条件，将其作为结果图像中对应模板位置的像素值；若不满足，则给结果图像中对应模板位置的像素赋予0。
（2）Sobel算子
Sobel算子是一种用于边缘检测的离散微分算子，它结合了高斯平滑和微分求导。该算子用于计算图像明暗程度近似值，根据图像边缘旁边明暗程度把该区域内超过某个数的特定点记为边缘。其算子模板为：
Alt
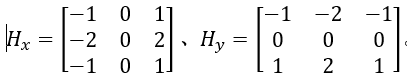
检测步骤：利用算子模板对图像进行卷积后叠加，判断结果是否大于阈值，若满足条件，将其作为结果图像中对应模板位置的像素值；若不满足，则给结果图像中对应模板位置的像素赋予0。
（3）拉普拉斯算子
拉普拉斯算子是一种无方向性的二阶导数算子，常用于图像增强领域和边缘提取。它通过灰度差分计算邻域内的像素。拉普拉斯运算只需要一个模板，所以计算量较小。拉普拉斯算子模板有: Alt

检测步骤：判断图像中心像素灰度值与它周围其他像素的灰度值，如果中心像素的灰度更高，则提升中心像素的灰度，反之降低中心像素的灰度，从而实现图像锐化操作；拉普拉斯算子通过对邻域中心像素的四方向或八方向求梯度，再将梯度相加起来判断中心像素灰度与邻域内其他像素灰度的关系；最后通过梯度运算的结果对像素灰度进行调整。
下图是各算子对图像边缘提取的结果图：
Alt

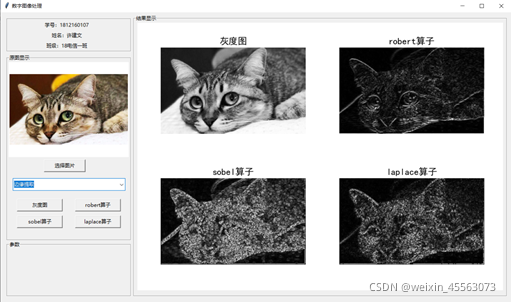
对比三个算子边缘提取的结果来看，Robert算子无法消除局部噪声干扰，也会丢失灰度值变化缓慢的局部边缘，从而导致边缘轮廓不连续；Sobel算子在较好的获取边缘效果的同时，对噪声具有一定的平滑作用，减小了对噪声的敏感性，但检测的边缘比较粗，会检测出一些伪边缘，边缘检测精度较低；拉普拉斯算子对图像中的阶跃型边缘点定位准确，对图像的噪声较敏感，它使噪声成分得到加强，这两个特性使该算子容易丢失一部分边缘的方向信息，造成一些不连续的检测边缘，同时抗噪声能力比较差，由于其算法可能会出现双像素边界，常用来判断边缘像素位于图像的明区或暗区，很少用于边缘检测。