目录
概要
整体架构流程
技术名词解释
技术细节
1.基本问题简介
2.线性失真
3.频率失真的危害
小结
概要
提示:这里可以添加技术概要
继续接着上一节的内容继续分享和学习,
整体架构流程
分三个部分,仔细的分享了失真方面的知识
技术名词解释
提示:这里可以添加技术名词解释
略
技术细节
1.基本问题简介
失真︰输出波形和输入波形的不一致,称为失真。但是这个不一致,不包括时间移位、幅度变化和幅度移位,比如准确放大的照片,虽与原始照片大小不一致,但不能称为失真。因此,对输出波形进行最优的线性运算后,仍和输入波形的不一致,称为失真。
任何一个运放或者其它放大器,只有做到"输入—输出"关系是曲线,当输入为单一频率纯净正弦波时,输出就一定不是正弦波,而是除基波之外,还包含谐波。这种失真的本质原因是放大电路"输入一输出"关系不是过零直线,因此也称之为非线性失真。
如果一个放大电路,"输入—输出"关系是一个过零的直线,当输入为纯净正弦波时,输出也是同频的纯净正弦波,这个放大电路称为"无非线性失真放大电路”。反之,则称为“具有非线性失真放大电路"。
2.线性失真
对于“无非线性失真放大电路”,仍会产生波形失真,此类失真称为"线性失真"。
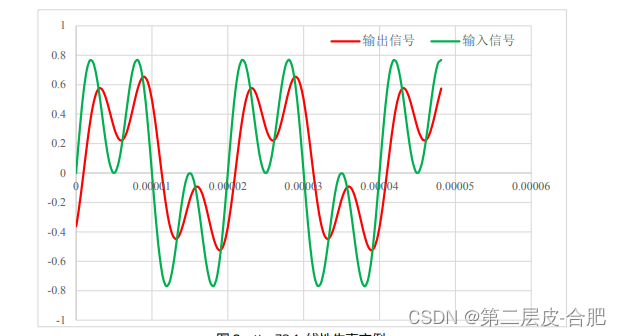
当输入不是纯净正弦波,而是几个正弦波的叠加,形成了如图Section76-1绿色曲线所示的复合波,放大电路对每个正弦波都不产生非线性失真,但是对每个正弦波的增益不同或者延时不同,造成输出波形变形,如图中红色曲线,这种失真叫频率失真,也称线性失真。
线性失真分为三种,
1)单独的幅度失真:放大电路对不同频率的输入信号,具有不同的放大倍数。
2)单独的相位失真︰放大电路对不同频率的输入信号,具有不同的延时。特别注意,不是"不同的相移”,而是"不同的延时”。
3)既有幅度失真,也有相位失真,称为综合失真。这是绝大多数情况。
对于我们常见的放大电路,理论上讲,绝不存在"无非线性失真放大电路”,因此如果输入波形为复合波,那么输出波形一定包含非线性失真,还包含线性失真,而线性失真中,一般既包含幅度失真,也包含相位失真。
3.频率失真的危害
失真度非常小的运算放大器,经过合适的负反馈后,可以使得放大电路的失真度进一步下降。很多优秀的放大电路,其失真度指标可以做到-120dB 以下,因此可以近似认为这就是"无非线性失真放大电路”。
但是,即便使用如此低失真度的放大电路,如果存在频率失真,也就是线性失真,输出波形仍然会发生不可逆的变形。
产生频率失真的根本要素是,输入波形是一个复合波,低失真度放大电路对输入波形中不同频率信号,实施了不同增益、不同延时的放大。虽然,对每个单一频率正弦波,都不产生非线性失真,但是,由于线性失真的存在,输出的复合波形仍然会发生变形。
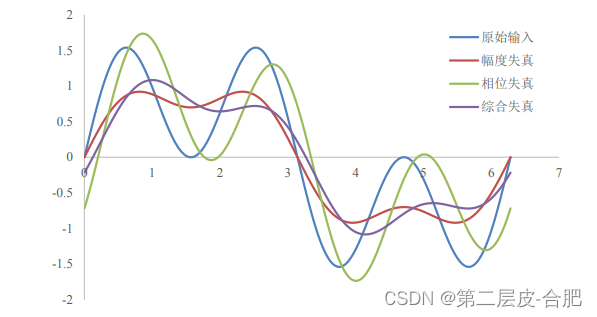
,表现线性失真的示意图。图中蓝色为原始输入的复合波形,由等幅度的基波和3次谐波相加形成,如果没有发生线性失真,其输出将与输入一样。单纯的幅度失真如图红色波形所示,它是1倍的基波+0.5倍的3次谐波组成,很显然,放大电路对3次谐波实施了幅度的衰减,输出波形看起来平滑了很多,即我们常说的高频抑制;而绿色波形则是单纯的相位失真,它是有1倍基波无相移·1倍3次谐波含一个固定相移组成;而紫色波形则是"既包含幅度失真,又包含相位失真"的综合失真。
小结
提示:这里可以添加总结
频率失真造成的危害是严重的。真正的放大电路,其输入信号一般不会是单一频率正弦波,虽然我们在做实验的时候广泛采用这种输入。比如音频放大电路,其输入信号是自然界的声音,它一定是包含很多频率分量的复合波。
以心电信号为例,其主要频率分量大致分布在0.1Hz~25Hz之间,为了可靠放大,一般会给信号链路中增加45Hz左右的低通滤波器,以抑制50Hz工频干扰以及更高频率的肌电信号﹔增加0.01Hz高通滤波器以抑制超低频率的信号漂移。这些滤波器的引入,一旦设计不好,就会对原始心电信号带来幅度的改变,或者相位的改变,进而引入线性失真,也就是频率失真。其直接后果就是,打印出来的心电信号发生了变形,误导了医生对病情的诊断。
产生频率失真的根本要素是,输入波形是一个复合波,低失真度放大电路对输入波形中不同频率信号,实施了不同增益、不同延时的放大。虽然,对每个单一频率正弦波,都不产生非线性失真,但是,由于线性失真的存在,输出的复合波形仍然会发生变形。
图Section76-2是用Excel生成的,表现线性失真的示意图。图中蓝色为原始输入的复合波形,由等幅度的基波和3次谐波相加形成,如果没有发生线性失真,其输出将与输入一样。单纯的幅度失真如图红色波形所示,它是1倍的基波+0.5倍的3次谐波组成,很显然,放大电路对3次谐波实施了幅度的衰减,输出波形看起来平滑了很多,即我们常说的高频抑制;而绿色波形则是单纯的相位失真,它是有1倍基波无相移·1倍3次谐波含一个固定相移组成;而紫色波形则是"既包含幅度失真,又包含相位失真"的综合失真。